Information Processing
Fibonacci Numbers:
Fibonacci
(real name Leonardo Bonacci) was a Italy mathematician
who developed the Fibonacci Sequence. It looks like this: 1, 1, 2, 3, 5, 8, 13,
21, 34…
Examples:
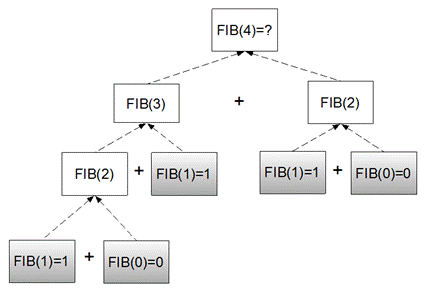
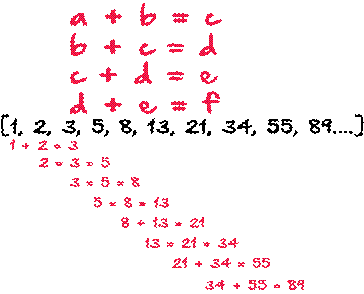
Real
life example for Fibonacci

Let us tabulate the Fibonacci
sequence and find a rule.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We observe
that the 3rd
term of the Fibonacci
sequence is the sum of 2nd term
and the 1st term.
|
F(1) |
F(2) |
F(3) |
F(4) |
F(5) |
F(6) |
F(7) |
… |
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
|
That is, F(3) = F(2) + F(1) and so we can extend and write the rule is
|
F(n)= F(n–1) + F(n–2) |
Where F(n) is the nth term
F (n–1) is the previous term to the nth term
F (n–2) is the term before the (n–1)
th term
This is how
the Fibonacci sequence is found.
Situation:
Let
us look at the family tree of a male drone bee and a female bee given below.
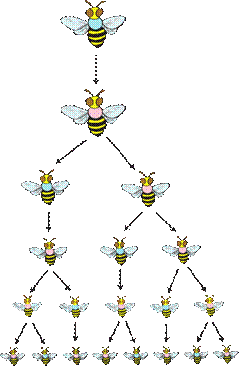
Here, female bees have 2 parents, a male
(drone) and a female whereas male (drone) bees have just one parent, a female.
(Males (drone) are produced by the queen’s unfertilized eggs, so male (drone)
bees only have a mother but no father!)
From
the picture the following points are noted:
1. The male A has 1 parent, a female A. The male B has 2 grandparents, since his mother had
two parents, a male A and a female.
The
male has 3 great-grandparents:
his grandmother had two parents but his grandfather had only one.
Now,
answer, how many great-great-grandparents did the male have?
Let us try to find the relationship among the pattern of bees
family by representing in the tabular form given below,
|
|
|
|
|
|
||||||
|
1 |
2 |
3 |
5 |
8 |
||||||
|
2 |
3 |
5 |
8 |
13 |
We see the Fibonacci numbers 1, 1,
2, 3, 5,… in the above table.
Bee population aren’t the only
place in nature where Fibonacci numbers occur, they also appear in the
beautiful shapes of trees, leaves, seeds, shells, storms and you… Yes! You are
an example of the beauty of the Fibonacci sequence. Th e human body has various
representations of the Fibonacci sequence proportions, from your face to your
ear to your hands and beyond! You have now been proven to be mathematically
gorgeous, so go forth and be beautiful! ...and maybe think math is a little bit
better than you first thought? Let us, learn about some more forms of the
Fibonacci sequence.
Patterns
in the Fibonacci sequence:
When we take any two successive (one after the other) Fibonacci numbers
and divide the larger by the smaller number the result of dividing the pairs of
numbers gives us the approximate value of the
Golden
ratio “phi” (φ) = 1.618. 1÷1=1, 2÷1=2,
3÷2=1.5, 5÷3=1.666.., 8÷5=1.6... 233÷144=1.618.... and so on.
This diagram
gives us an idea of the proportions of a Golden Rectangle. It is divided into
two pieces, and the ratio of the two parts (a to b) is
the Golden Ratio. If we
investigate even further, we will find that the two parts together (a + b) is
the same ratio to just the left part (a)
For example,
Let us take 8th and 9th Fibonacci
numbers where a = 34 and b = 21
(i)
a÷b=34÷21=1.61
(ii)
(a+b) ÷ b= (21+34) ÷ 34=1.61
Therefore we
conclude that a÷b = (a+b)÷b= (φ) = 1.61 Th e Fibonacci numbers
will also create the Golden Spiral as
shown in the snail picture.
