Life Mathematics
Percentage
It
is used to find the amount or share of something
in terms of 100. In its simplest form, percent means per hundred. To express a
number between zero and one, percentage formula is used.
It is
defined as a number represented as a fraction of 100. Denoted by the symbol =
%, the percentage is majorly used to
compare and find out ratios.
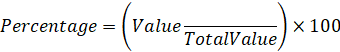
Q1.Express ![]() as a percentage.
as a percentage.
Solution:
![]() )
)
![]()
![]()
Q2. There are 150
students in a class. Out of them, 75 are girls. Find the percentage of girls in
the class?
Solution:
Total students in the class=150
Girls in the class = 75
% of girls in the class = (75 ⁄ 150)
× 100 = (7500 ⁄ 150) = 50%
Percentage Increase
It is the
ratio of value increased to the original value and multiplied by 100. It is
expressed in percentage. If there is an increase in the value of anything, then
there is an increase in percentage.
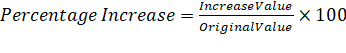
Q.
What is the percentage change in the rent of the house if on the month of
January it was Rs. 10,000 and in the month of March it is Rs. 15,000.?
Solution:
We
can clearly see that there is an increase in the value of rent, so the
percentage increase will be given as:
Percentage Increase
= (Increased Value ⁄ Original Value) × 100
Here,
Increased value = 15000 – 10000 = 5000
Original
Value = 10000
5000
⁄ 10000 = 33.33%
Hence,
there is a 33.33% increase in the value of rent.
Percentage Decrease:
When there is a decrease in the value of something, then, to know the
percentage decrease, that is, to know the decrease per hundred, – this formula
is used. It is the ratio of the decrease of the decreased value to the original
value multiplied with 100.
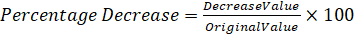
1.
Few days ago,
the cost of mangoes per 100 kg was Rs. 10000. Now is it being sold at rs. 8000. What is the percentage decrease in the value?
Solution:
Percentage decrease in the
land value
=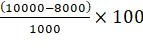
=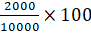
=
0.2 × 100
=
20%
So
there is a 20% decrease in value of 100 kg mangoes.
Some Solved Examples:
In an election, candidate A got 75%
of the total valid votes. If 15% of the total votes were declared invalid and
the total numbers of votes is 560000, find the
number of valid vote polled in favour of candidate.
Solution:
Total
number of invalid votes = 15 % of 560000
= 15/100 ×
560000
= 8400000/100
= 84000
Total
number of valid votes 560000 – 84000 = 476000
Percentage
of votes polled in favour of candidate A = 75 %
Therefore,
the number of valid votes polled in favour of candidate A = 75 % of 476000
=
75/100 × 476000
=
35700000/100
=
357000
A shopkeeper bought 600 oranges and
400 bananas. He found 15% of oranges and 8% of bananas were rotten. Find the
percentage of fruits in good condition.
Solution: Total
number of fruits shopkeeper bought = 600 + 400 = 1000
Number
of rotten oranges = 15% of 600
= 15/100 × 600
= 9000/100
= 90
Number
of rotten bananas = 8% of 400
= 8/100 × 400
= 3200/100
= 32
Therefore,
total number of rotten fruits = 90 + 32 = 122
Therefore
Number of fruits in good condition = 1000 - 122 = 878
Therefore
Percentage of fruits in good condition = (878/1000 × 100)%
= (87800/1000)%
= 87.8%
2.
Profit & Loss
Cost
Price (C.P)- The amount for which an article is bought is called its Cost Price
(C.P)
Selling
Price (S.P)- The amount for which an article is sold is called its Selling
Price (S.P)
Profit/Gain-When
the S.P is more than the C.P, then there is a profit or gain.
![]()
Loss-
When the S.P is less than the C.P, then there is a loss.
![]()
Some
important Formulae:
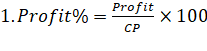
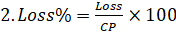
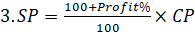
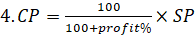

Q1. Henry sold a bicycle at 8% gain. Had
it been sold for $ 75 more, the gain would have been 14%. Find the cost price
of the bicycle.
Solution:
Let the cost price of the bicycle be $
x.
SP of
the bicycle at 8% gain = $ [{(100 + gain %) /100} × CP]
= $ [{(100 + 8)/100} × x]
=
$ {(108/100) × x}
= $ (27x/25)
SP of the bicycle at 14% gain = $ [{(100 +
14)/100} × x]
= $ {(114/100) × x}
= $ (57 x/50)
Therefore,
(57 x /50) - (27 x/25) = 75
⇔ (57 x – 54 x)/50 = 75
⇔ 3 x = (50 × 75)
⇔ x = (50 × 25)
⇔ x = 1250
Hence
the CP of the bicycle is $ 1250.
Q2. Suppose a shopkeeper has bought 1 kg of apples for 100
rs. And sold it for 120 kg. How much is the profit he got?
Solution:
Cost
Price for apple is 100 rs.
Selling
Price for apple is 120 rs.
Then
profit gained by shopkeeper is; P = SP – CP
P
= 120 – 100 = Rs. 20/-

What is a Discount?
Discount means
reducing the price or value of an object or item. In other words, In order to increase the sale and also to clear the
old stock, a certain percentage of rebates on the marked price of the articles.
This rebate is known as discount.
Marked
Price-
The price on the label of an article/product is called the marked
price or list price. This is the price at which product is intended to be sold.
However, there can be some discount given on this price and the actual selling price of the
product may be less than the marked price. It is generally denoted by MP.
When Discount is offered, M.P. > S.P.
When Discount is not offered, M.P. <
S.P.
Discount = Marked Price – Selling Price
Discount percentage =
[(Discount)/(Marked price)]× 100.
Discount =
Discount % of Marked Price
Additional
expenses made after buying an article are included in the cost
price and are known as overhead expenses.
·
cost price = buying price + overhead expenses
Sales Tax is charged on the sale of an
item by the government and is added to the Bill Amount.
·
Sales tax = Tax% of sale amount.
Q1. Akshay offers a discount of 20% on all the items at her shop and still
makes a profit of 12%. What is the cost price of an article marked at Rs 280?
Solution:
We have the Marked Price = Rs 280.
Also we have the Discount = 20% of Rs 280.
Thus we can write it as = (20/100) × 280 =
Rs 56.
So the selling price = Rs (280 – 56) = Rs
224.
Let the cost price be Rs 100.
Profit = 12% of Rs 100 which is = Rs 12.
So selling price = Rs (100 + 12) = Rs 112.
Now
let us see further:
If the selling price is Rs 112, cost price
= Rs 100.
If the selling price is Rs 224, cost price
= Rs (100/224) × 112 which is = Rs 200.
Ans=Rs 200
Q2. A bicycle marked at Rs
1,500 is sold for Rs 1,350. What is the percentage of the discount?
Solution:
Marked
Price = Rs 1500, and Selling Price = Rs 1350.
Amount
of discount is = Marked Price – Selling Price.
In other words we can say that = (1500 – 1350)
= Rs 150.
Discount
for Rs. 1500 =Rs 150
Therefore, the Discount for Rs 100 = (150/1500) × 100 = 10%
Thus, the Percentage of discount = 10%
Q3. An almirah is sold at
Rs 5,225 after allowing a discount of 5%. Find its marked price.
Solution:
The discount is given in percentage.
Hence, the M.P. is taken as Rs 100. Rate of discount = 5%.
Amount of discount = (5/100)
×100 = Rs 5.
Selling Price = M.P. –
Discount = 100 – 5 = Rs. 95.
If S.P. is Rs 95, then M.P. is
Rs. 100.
When S.P. is Rs.
5225, M.P. = Rs. (100/95) × 5225.
Therefore
the M.P. of the almirah = Rs. 5,500
3. Simple & Compound Interest:
Simple Interest is the rate at which we lend or
borrow money.
Let the principal amount be equal to P. Let the rate at which the
interest is levied is equal to R% per annum (per
year). let the time for which the amount is lent = T
years. Then we can write:
Simple Interest = [{P×R×T}/100]
Compound interest (or compounding interest) is interest calculated on
the initial principal, which also includes all of the accumulated interest of
previous periods of a deposit or loan.
Compound Interest = Total amount of Principal and Interest in future (or
Future Value) less Principal amount
at present (or Present Value)
= [P (1 + i)n] –
P
= P [(1 + i)n –
1]
(Where P = Principal, i = nominal annual interest rate in
percentage terms, and n = number of compounding periods.)
Q. A bank offers 5%
compound interest calculated on half-yearly basis. A customer deposits Rs. 1600
each on 1st January and 1st July of a year. At the end
of the year, the amount he would have gained by way of interest is:
Solution:
Amount after 1 year on Rs. 1600 (deposited on 1st Jan) at 5% when
interest calculated half-yearly
=P (1+(R/2)100)^2T
=1600(1+
(5/2)100)^2×1
=1600(1+140)
^2
=P
(1+(R/2)100) ^2T
=1600(1+
(5/2)100) ^2×1
=1600(1+140)
^2
Amount
after 1/2 year on Rs. 1600 (deposited on 1st Jul) at 5% when interest
calculated half-yearly
=P (1+(R/2)100)^2T
=1600(1+
(5/2)100) ^2×12
=1600(1+140)
=P
(1+(R/2)100) ^ 2T
=1600(1+
(5/2)100) ^2×12
=1600(1+140)
Total
Amount after 1 year
=1600(1+140)2+1600(1+140)
=1600(4140)2+1600(4140)
=1600(4140)
[1+4140]
=1600(4140)
(8140)
=41×81=Rs. 3321
=1600(1+140)2+1600(1+140)
=1600(4140)2+1600(4140)
=1600(4140)
[1+4140]
=1600(4140)
(8140)
=41×81
=Rs. 3321
Compound Interest = Rs.3321 - Rs.3200 = Rs.121