STATISTICS

1 Data:

Data is the basic unit in Statistics. Data is a collection of facts such as numbers, words, measurements and observations. It must be organised, for it to be useful and to get information. Data can be collected in many ways. Among all the ways, direct observation is one of the simplest way to collect the data.

For example, if you want to find the number of types of houses in a village, You can count the types of houses in the village, in person similarly,

(i) Collection of brand wise motorcycles in your place.

Brand A – 25, Brand B – 40, Brand, C –14 and Brand D – 37

(ii) Collection of term marks in Mathematics of your class mates.

39, 20, 19, 47, 50, 26, 35, 40, 17, 25, 41.

(iii) Number of students playing different sports from your class.

Volley ball –12 Kabaddi – 10 Hockey – 9 Cricket – 7 Badminton – 7

(iv) Staff ’s age in a company

27, 51, 19, 21, 46, 35, 52, 25, 57, 29.

The above facts are some more examples for data,

Let us now see the kinds of data. There are two kinds of data namely primary data and secondary data.

Primary data:

These are the data that are collected in person for the first time for a specific purpose. Here, Kamaraj has collected the data of math marks from the students in person. It is called primary data.

Also, (i) Census in a village

(ii) Collection of colours which the students like in a class are some examples of primary data.

Secondary data:

These are the data that are sourced from some places that has originally collected it. This kind of data has already been collected by some other persons. The statistical operation may have been performed on them already. Here, Geetha also collected the data but she took it from a record which had already collected them. This is called secondary data.

Also, (i) The details of 'PATTA' for a land can be had from the registration office.

(ii) Birth–Death details data can be got from concern office are some examples of secondary data.

2.Data in Tabular form

To make the given data easily understandable, we tabulate the data in the form of tables or charts. A table has three columns that contains

(i)Variable /Class (ii) Tally Marks (iii) Frequency

Variable / Class:

Arrange the given data from the lowest to the highest in the first column under the heading variable or class.

Tally Marks:

A vertical line(|) which is marked against each item falling in the variable /class is called tally marks.

Frequency:

The number of times an observation occurs in the given data is called the frequency of the observation. This is easily counted from the tally marks column.

For example:

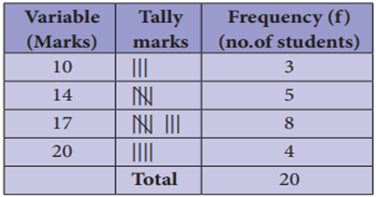
From the table, we understand that three students got 10 marks, five students got 14 marks and so on.

Ungrouped data or Discrete Data:

An ungrouped data can assume only whole numbers and exact measurement. These are the data that cannot have a range of values. A usual way to represent this is by using Bar graphs

Examples: 1. The number of teachers in a school.

2. The number of players in a game.

Grouped data or Continuous Data:

A grouped data is any value within a certain interval. The data can take values between certain range with the highest and the lowest value. Continuous data can be tabulated in what is called as frequency distribution. They can be graphically represented using Histograms.

Example: 1. The age of persons in a village.

2. The height and the weight of the students of your class.

3 Frequency distribution table

Frequency distribution:

A frequency distribution is the arrangement of the given data in the form of the table showing frequency with which each variable occurs.

If we have more number of students in the class , it would be very difficult to understand and to get information unless it is organised. For this reason, we organise larger data into a table called the frequency distribution table. Therefore, the tabular arrangement which shows the observations and their frequency of occurrences is called the frequency distribution table. There are two types of distribution table namely

(i) frequency distribution table for ungrouped data and

(ii) frequency distribution table for grouped data.

3.1 Construction of frequency distribution table for ungrouped data.

Example 1 Form an ungrouped frequency distribution table for the weight of 25 students in STD IV given below and answer the following questions.

25, 24, 20, 25, 16, 15, 18, 20, 25, 16, 20, 16, 15, 18, 25, 16, 24, 18, 25, 15, 27, 20, 20, 27, 25.

(i) Find the range of the weights.

(ii) How many of the students has the highest weight in the class?

(iii) What is the weight to which more number of students belong to?

(iv) How many of them belong to the least weight?

Solution:

To form a distribution table, arrange the given data in ascending order under Weight column then, put a vertical mark against each variable under Tally marks column and count the number of tally marks against the variable and enter it in Frequency column as given below. Hence, the distribution table is

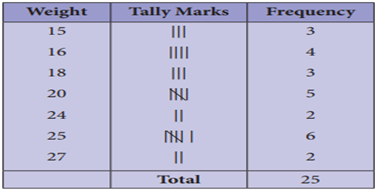
Thus, we can tabulate the above table as follows.

(i) The range of the given data is the difference between the largest and the smallest value. Here, the range = 27–15 =12.

(ii) From this table, two of the students have the highest weight of 27 kg.

(iii) 6 students belong to 25 kg weight.

(iv) 3 students belong to the least weight of 15 kg.

3.2 Construction of frequency distribution table for grouped data:

Now, we will consider a situation, if we collect data of marks for 50 students, it becomes very difficult to put tally for each and every marks of all the 50 students. Because if we arrange the marks in a table, it will be very large in length and not understandable at once. In this case, we use class intervals. In this table, consider the groups of data in the form of class intervals to tally the frequency for the given data.

Class Interval:

The range of the variable is grouped into number of classes, and each group is known as class interval (C.I). The difference between the upper limit (U) and the lower limit (L) of the class is known as class size. i.e. C.I = Upper limit – Lower limit

For example,

Marks for the C.I 10 to 20 can be written as 10-20, whose class size is 20–10=10

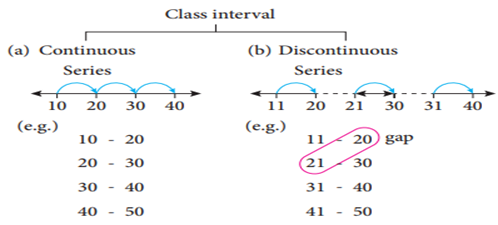
(a) While distributing the frequency, we follow the counting as given below. Suppose the classes are 10-20, 20-30, 30-40, 40-50 ..... This represent a continuous series. Here, 20 is included in the class 20-30 and 30 is included in 30-40, likewise for the other classes also.

(b) In case the given series has a gap between the limits of any two adjacent classes, this gap may be filled up by extending the two limits of each class by taking half of the value of the gap. Half of the gap is called the adjustment factor.

Conversion of a discontinuous series into continuous series:

In case the given series is a discontinuous, we can make it as continuous as follows,

Illustration: 1

11 - 20 gap difference in the gap = 21 – 20=1

21 - 30

31 - 40

41 - 50

Lower boundary = lower limit –half of the gap

Upper boundary = upper limit + half of the gap

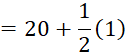
Therefore, the class interval can be changed into a continuous one as given in the following table,

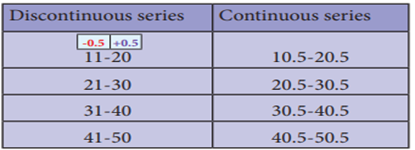
(i).Construction of grouped frequency distribution table – Continuous series.

Example 2 The EB bill (in ₹) of each of the 26 houses in a village are given below. Construct the frequency table.

Solution:

Maximum bill amount = ₹800

Minimum bill amount = ₹120

Range = maximum value – minimum value Range = 800 – 120 = ₹680

Suppose if we want to take class size as 100, then the

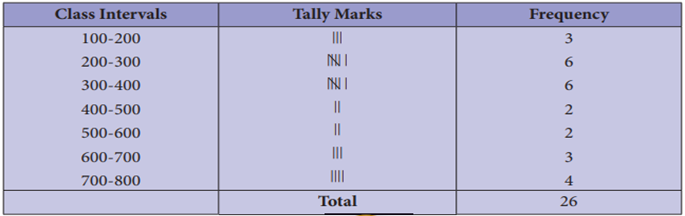
(ii).Construction of grouped frequency distribution table - Discontinuous series.

Example 3 Construct a continuous series frequency distribution table.

Solution:

As told above, first we should fill the gap by extending the two limits of each class by half of the value of the gap. Here the gap is 1, so subtracting and adding half of the gap i.e 0.5 to the lower and the upper limit of each class makes it as a continuous series.

4.Graphical representation of the frequency distribution for ungrouped data

A graphical representation is the geometrical image of a set of data. It is a mathematical picture. It enables us to think about a statistical problem in visual terms. A picture is said to be more effective than words for describing a particular thing. The graphical representation of data is more effective for understanding. Now, we are going to represent the given ungrouped data in the circular form namely the pie diagram or the pie chart.

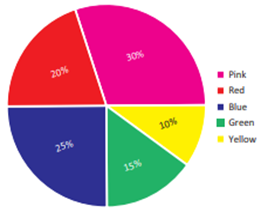
5 Pie chart (or) Pie diagram

A pie chart is a circular graph which shows the total value with its components. The area of a circle represents the total value and the different sectors of the circle represent the different components. The circle is divided into sectors and the area of the sectors is proportional to the information given. In the ‘pie chart’ the data are mostly expressed in percentage. Each component is expressed as percentage of the total value.

The Pie diagram is so called because the entire graph looks like an American food ‘pie’ and the components resemble slices cut from ‘pie’.

Example

5.1 Method of constructing a pie chart:

In a pie chart, we know that the various components are represented by the sectors of a circle and the whole circle represents the sum of the value of all the components. Therefore, the total angle of 360° at the centre of the circle is divided into different sectors according to the value of the components.

The central angle of a component

Sometimes, the value of the components are expressed in percentage. In such cases,

The central angle of a component

Steps for construction of the pie chart:

1) Calculate the central angle for each component using the above formula and tabulate it.

2) Draw a circle of convenient radius and mark one horizontal radius in it.

3) Draw radius making central angle of first component with horizontal radius. This sector represents the first component. From this radius, draw next radius with central angle of the second component and so on, until the completion of all components.

4) For identification of each sector, shade with different colours.

5) Label each sector.

Here are given some examples, let us draw the pie chart for the given data.

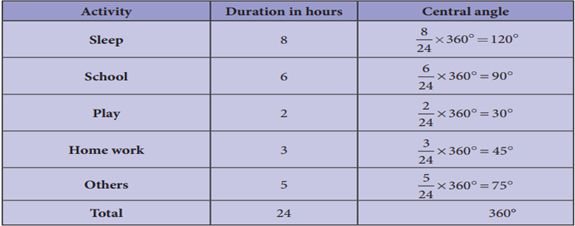
Example 4 The number of hours spent by a school student on various activities on a working day is given below. Construct a pie chart.

1. Find the percentage of sleeping hours.

2. By what angle is home work more than play?

3. By what angle are other activities less than sleep?

Solution:

Number of hours spent in different activities in a day of 24 hours are converted into components parts of 360°.

The time spent by a school student during a day (24 hours)

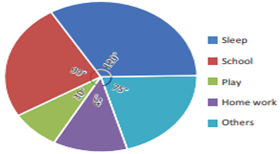
1. The percentage of sleeping hours = × 100 = 33.33%

2. Home work is 45°–30°=15° more than play

3. Other activities are 120°–75°=45° less than sleep.

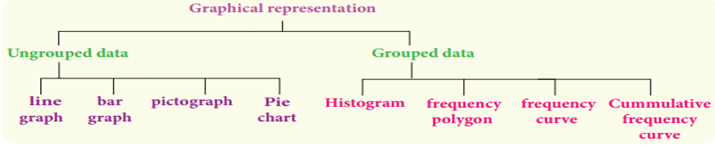
6 Graphical representation of the frequency distribution for grouped data

The Line graph, Bar graph, Pictograph and the Pie chart are the graphical representations of the frequency distribution for ungrouped data. Histogram, Frequency polygon, Frequency curve, Cumulative frequency curves (Ogives) are some of the graphical representations of the frequency distribution for grouped data.

In this class, we are going to represent the grouped data frequency by Histogram and Frequency polygon only. You will learn the other type of representations in the higher classes.

7 Histogram

A histogram is a graph of a continuous frequency distribution. Histogram contains a set of rectangles, the base of which is the length of the class interval and the frequency in each class interval is its height. i.e the class intervals are represented on the horizontal axis (x- axis) and the frequencies are represented on the vertical axis (y-axis).

The area of each rectangle is proportional to the frequency in the respective class interval and the total area of the histogram is proportional to the total frequency. Because of the continuous frequency distribution, the rectangles are placed continuously side by side with no gap between adjacent rectangles.

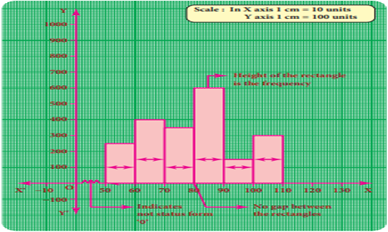
Steps to construct a Histogram:

1. Represent the data in the continuous form (exclusive form) if it is in discontinuous form (inclusive form) by converting it using the adjustment factor.

2. Select the appropriate units along the x-axis and y-axis.

3. Plot the lower limits of all class interval on the x –axis.

4. Plot the frequencies of the distribution on the y – axis.

5. Construct the rectangles with class intervals as bases and corresponding frequencies as heights. Each class has lower and upper values. This gives us two equal vertical lines representing the frequencies. The upper ends of the lines are joined together and this process will give us rectangles.

7.1 Construction of a histogram for continuous frequency distribution:

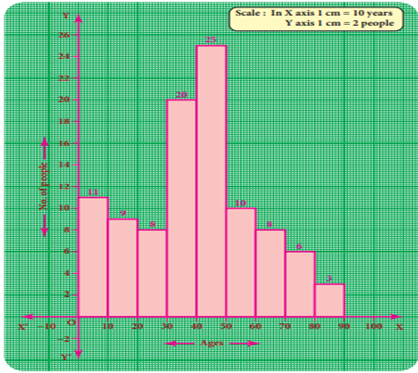
Example 5 Draw a histogram for the following table which represents the age groups from 100 people in a village.

Solution:

The given data is a continuous frequency distribution. The class intervals are drawn on x-axis and their respective frequencies on y-axis. Classes (ages) and its frequencies (number of people) are taken together to form a rectangle.

The histogram is constructed as given below

7.2 Construction of histogram for discontinuous frequency distribution:

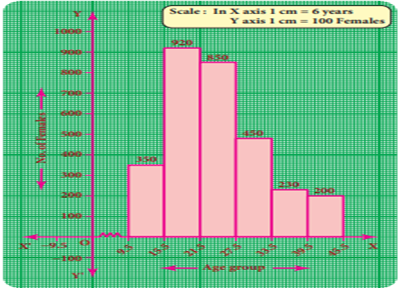
Example 6 The following table gives the number of literate females in the age group 10 to 45 years in a town.

Draw a histogram to represent the above data

Solution:

The given distribution is discontinuous. If we represent the given data as it is by a graph we shall get a bar graph, as there will be gaps in between the classes. So, convert this into a continuous distribution using the adjustment factor .

That is, lower boundary = lower limit

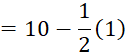
Upper boundary = upper limit

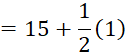
The first class interval can be written as 9.5-15.5 and the remaining class intervals are changed in the same way. There are no changes in frequencies.

The new continuous frequency table is

The histogram is constructed as below

8 Frequency Polygon

A frequency polygon is a line graph for the graphical representation of the frequency distribution. If we mark the midpoints on the top of the rectangles in a histogram and join them by straight lines, the figure so formed is called a frequency polygon. It is called a polygon as it consists of a number of lines as the sides of a polygon.

A frequency polygon is useful in comparing two or more frequency distributions. A frequency polygon for a grouped frequency distribution can be constructed in two ways.

i) Using a histogram

ii) Without using a histogram

8.1 To construct a frequency polygon using a histogram:

1. Draw a histogram from the given data.

2. Join the consecutive midpoints of the upper sides of the adjacent rectangles of the histogram by the line segments.

3. It is assumed that the class interval preceding the first rectangle and the class interval succeeding the last rectangle exists in the histogram and the frequency of each extreme class interval is zero. These class intervals are known as imagined class intervals.

4. To get frequency polygon, join the midpoints of these imagined classes with the corresponding midpoints of the upper sides of the first and last rectangles of the histogram.

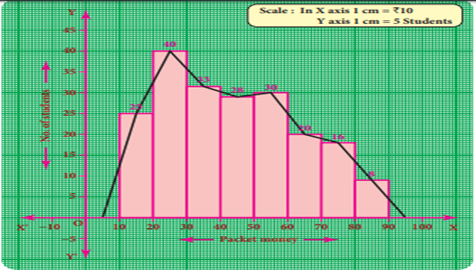
Example 7 The following is the distribution of pocket money of 200 students in a school.

Draw a frequency polygon using histogram.

Solution:

Represent the pocket money along x- axis and number of students along the y–axis.

Draw a histogram for the given data. Now, mark the midpoints of the upper sides of the consecutive rectangles. Also mark the midpoints of two imagined class intervals 0-10 and 90-100 whose frequency is 0 on x- axis. Now, join all the midpoints with the help of ruler. We get a frequency polygon imposed on the histogram.

8.2 To draw a frequency polygon without using a histogram:

(1) Find the midpoints of the class intervals and tabulate it.

(2) Mark the midpoints of the class intervals on x-axis and frequencies on y-axis.

(3) Plot the points corresponding to the frequencies at each midpoints.

(4) Join the points using a ruler, to get the frequency polygon.

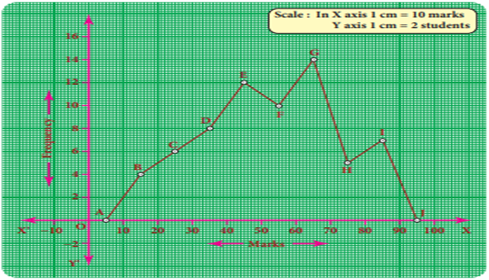
Example 8 Draw a frequency polygon for the following data without using histogram.

Solution:

Find the midpoint of the class intervals and tabulate it

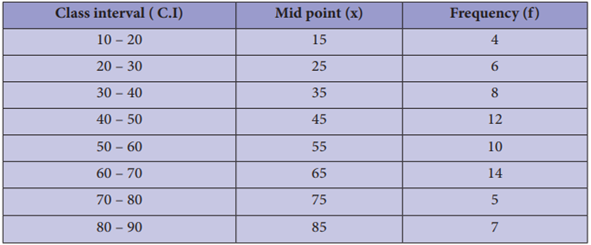
The points are (15,4) (25,6) (35,8) (45,12) (55,10) (65,14) (75,5) (85,7).

In the graph sheet, mark the midpoints along the x- axis and the frequency along the y- axis.

We take the imagined class as 0 – 10 at the beginning and 90 – 100 at the end , each with frequency ‘zero’.

From the table, plot the points. We draw the line segments AB, BC, CD, DE, EF, FG, GH, HI, IJ to obtain the required frequency polygon ABCDEFGHIJ.