INFORMATION PROCESSING

1 Introduction

Before spending your money to shop any items from a market or a departmental store, consider the best prices, the best quality and other reliable things. This is wise shopping.

The best way of shopping is comparing goods means its price, quality, quantity, offers, discount and other considerable things.

Here we learn, how to be a wise consumer before shopping a product from the following situation.

Shopping comparison:

Situation 1:

Imagine that the teacher appoints you and your friend to be an incharge of the fruit section of your school canteen for a week. she also instructs the following steps, and she can help you when needed.

v Now you have to buy fruits for 2 days as per your shopping list.

v One of you should go to the market and the other should go to the departmental store to know the cost of the fruits before shopping.

v Estimate yourselves which place will give you the best deal. After that,

v Check your shopping list to see how much fruits you required.

v Compare the weight and price for each item from both places.

v Select the best deal for all items in only one place .

v Discuss and compare the price list so that you decide where to buy the required list of fruits

Shopping list

1. 20 kg apples

2. 20 kg of guavas

3. 30 boxes of strawberries

4. 20 dozens of bananas

For example, the collected model price list from both shops is given in the table below:

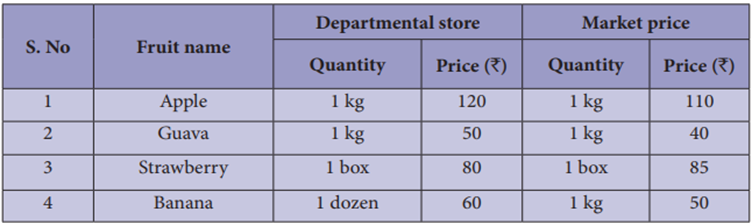
Now, we will calculate the total price of the required and quantity of fruits from both the departmental store and market.

Calculating the Departmental store Price:

Apple

ü Cost of 1 kg of apples = ₹120

ü Cost of 20 kg of apples = 20 × 120 = ₹2400

Total Price=₹2400

Guava

ü Cost of 1 kg guavas = 50

ü Cost of 20 kg guavas = 20 × 50 = 1000

Total Price=₹1000

Strawberry

ü Cost of 1 box of strawberries = 80

ü Cost of 30 boxes of strawberries = 30 × 80= 2400

Total Price=₹2400

Banana

ü Cost of 1dozen of bananas = 60

ü Cost of 20 kg of bananas = 20 × 60 = 1200

Total Price=₹1200

Calculating the Market Price:

Apple

ü Cost of 1 kg apples = 110

ü Cost of 20 kg of apples = 20 × 110 = 2200

Total Price=₹2200

Guava

ü Cost of 1 kg guavas = 40

ü Cost of 20 kg guavas = 20 × 40 = 800

Total Price=₹800

Strawberry

ü Cost of 1 box of strawberries = 85

ü Cost of 30 boxes of strawberries = 30 × 85 = 2550

Total Price=₹2550

Banana

ü Cost of 1 kg of bananas = 50

ü Cost of 20 kg of bananas = 20 × 50 = 1000

Total Price=₹1000

Now, let us compare the shopping price of the Departmental store to that of the Market shop price.

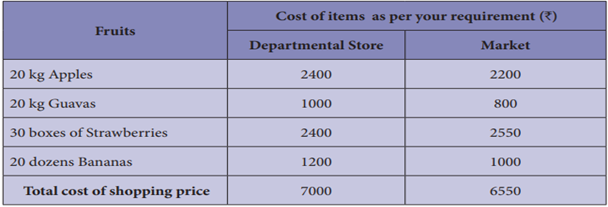
From the above comparison, we find that shopping made at the Market shop is the best deal quantity wise as well as in price and hence it is a wise decision to shop in the Market.

Comparing containers of different size:

Many times, items are packed in different size of containers.

v Sometimes shoppers save money by selecting a larger container of the same item. For example, 5 units of 200ml pack of milk often costs more than 1 litre of milk.

v Sometimes a store has two prices for the same item. One price is for buying a single item, while the other price is for buying more than one of that item. For example, groundnut oil may cost ₹135 for 1 litre bottle and ₹240 for 2 litre bottles. In this case, if you buy two 1 litre bottles, you will pay more. Sometimes, buying in quantity saves money.

v Some times the consumer may not be able to use up the larger size of an item before it becomes stale or outdated. To find out which size container is the best to buy, you will need to know the price of single pack of the contents.

2 Packing

When we are packing something in a box or suitcase or cupboard, first we have to decide how we are going to pack. How many items can be fitted into that fixed space? A good example of this is, before you go to school, you try to pack everything you need (like your books, notebooks, geometry box, sports equipment, food and water bottle) into your school bag. At that time, you are very clear that your books should not be damaged and you are able to carry everything yourself.

Apart from these, the packaging method is used in many cases. Such as cutting of sheets, glass, paper, wood, cloth or other materials and room allotment, seating arrangement in the particular space provided, parking vehicles with proper lanes and saving data in hard disk, CD, pen drive and so on.

Using some packing methods, from the following situations and examples, let us try to understand how best to fit the items into the space in the containers or in rooms or in boxes etc.,

3 Packaging Methods

Fractional Method:

Here, when we fill items in bags or in containers, we determine the weight, value and number of each item with the condition that the total weight of the container is less than or equal to a given limit and the total value is as large as possible. Fractional method uses the technique of buying things fractionally and admits buying of more items within a given budget. Let us learn more about this method from the following situation.

Situation 1

Suppose that you want to buy some vegetables and fruits that are given in the picture with their weights and price and you have a bag that capacity of carrying 15 kg. The objective is to buy the more items within your budget ₹550 and also weight should not exceeding 15 kg.

You cannot buy all the items, because if you calculate the total weight of all the items, then it would be greater than 15 kg (extreme capacity of your bag is 15 kg). So, let us try some approaches, to find how you can select more items so that you will buy them with maximum price within your budget of ₹550. For that let us tabulate the items with their weights and price you want to buy.

I Approach - Selecting items with maximum price

In this approach, we select the items according to the maximum price. Here the maximum price in the table is ₹150/-. Now, let us tabulate to find the total price and how much can we buy vegetables and fruits within our budget and not exceeding 15kg.

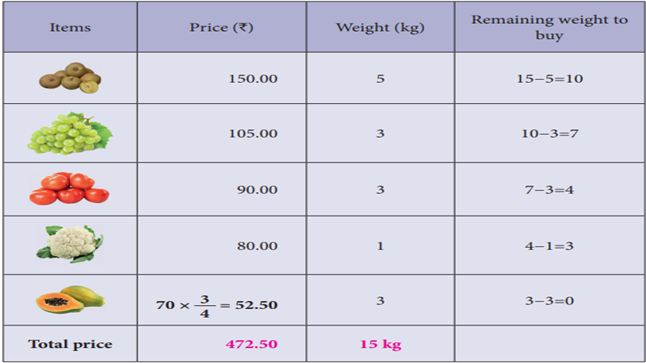
Here, 3kg of papaya is enough as the total weight reaches 15kg. So, 3kg of papaya costs ₹52.50. Hence, in this approach, we will spend maximum ₹472.50 to buy 15kg of vegetables and fruits.

II Approach - Selecting items with minimum weight

In this approach, we select the items according to the minimum weight. Here, we can select more and more items. Now, let us tabulate to find the total price and how much can we buy vegetables and fruits within our budget and not exceeding 15kg.

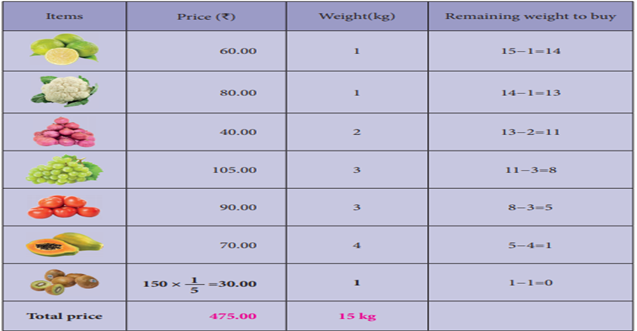
Here, 1 kg of Sapota is enough to complete 15 kg with minimum price of ₹30 per kg. Hence in this approach, we will spend maximum ₹475 to buy 15 kg of vegetables and fruits.

III. Approach - Finding the maximum price to weight ratio.

In this approach, we select the items according to the maximum price to weight ratio (find the rate of 1kg). Now, let us tabulate to find the total price and how much can we buy vegetables and fruits within our budget and not exceeding 15 kg.

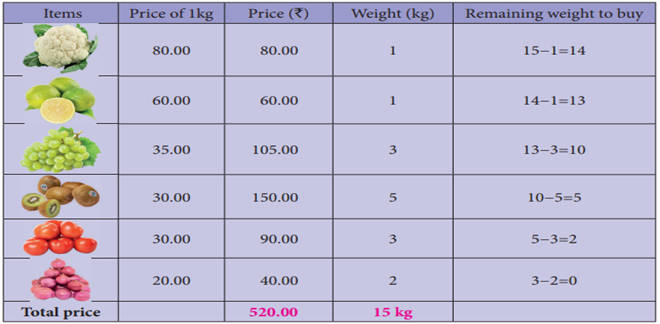
In this approach, we can buy all vegetables and fruits except papaya as we need with maximum price within our budget and not exceeding 15 kg. Comparatively, in the II approach we can buy more items but spend minimum amount only. So, we can say third approach is best one.

Sorting Method:

Situation 2:

Consider that you are going on a field trip in your school and you have six groups of students of group sizes as given below.

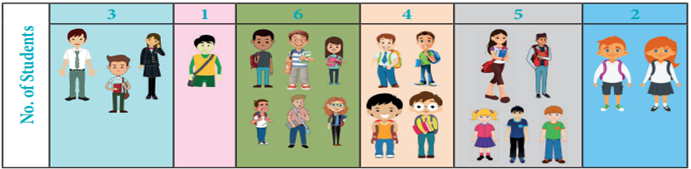
You need to fit the group of students in a cab that has a capacity of seven members. How many cabs would you need to arrange so that each group stays together? To solve this problem, we have to remember two things, one is minimum number of cabs to be used and another thing is each group of students stays together. For these purposes, the packing methods will help us.

There are two packing methods in common use. They are:

(i) First-fi t method

(ii) (First-fi t decreasing method

Before we try to solve this problem using one of these packing methods, one thing we need to know is finding the minimum required.

What is the minimum required in this problem is the number of cabs. So, to calculate the minimum number required, we have to add up the total number students and divide by the seeking capacity of a cab.

Here, the total number of students = 3+1+6+4+5+2 = 21

Capacity of seater of a cab = 7

Therefore, the cab minimum required = 21÷ 7 = 3 cabs.

Now, we don’t know whether 3 cabs can be an answer to this problem. 3 cabs may or may not be enough to accommodate when the group of students stays together. Let us go on to apply the methods now one by one.

First-fi t method:

Step 1. Take the group of students in the order given.

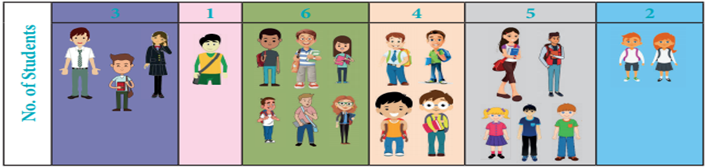
Step 2. Place each group of students in the fi rst cab and continue trying to a fi t them in the cabs where there is still space for each group and till, all are placed as shown in the picture below.

From the above picture, observe the following:

Group 1 – 3 students - accommodate them into 1st cab, so that the remaining seats are 4.

Group 2 – 1 student - also accommodate him into 1st cab,so that the remaining seats are 3.

Group 3 – 6 students - As there are no enough seats in the 1st cabs and so accommodate them into 2nd cab, so that remaining seat is 1.

Group 4 – 4 students - Since there are no enough seats in the fi rst 2 cabs and so accommodate them into 3rd cab, so that remaining seats are 3.

Group 5 – 2 students – As there are enough seats in the 1st cab, accommodate them into 1st cab, so that remaining seat is 1.

Group 6 – 5 students -Since there are no enough seats in all the 3 cabs and so accommodate them into 4th cab, so that remaining seat is 1.

Using this First- fit method, we need 4 cabs and there are 1+1+3+2=7 seats still remaining to be fi lled and we can say that the seats are not utilized to the optimum level.

Let us now see the other method.

First-fit decreasing method:

Step 1. Re-order the group of students so that they are in descending order.

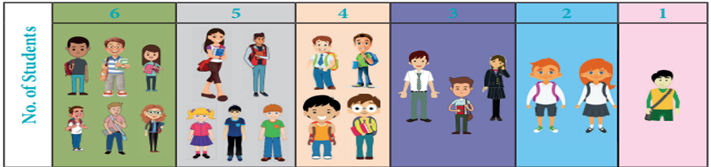
Step 2. Do the same process of the first fi t method to the re-ordered group. Place each group of students in the first cab and continue trying to fi t them in the cabs where there is still space and all are placed as shown in the picture below.

From the above picture, we observe that:

Group 3 – 6 students - accommodate them into 1st cab so that the remaining seat is 1.

Group 6 – 5 students - As there are no enough seats in the 1st cab and so accommodate them into 2nd cab and the remaining seats are 2.

Group 4 – 4 students - As there are no enough seats in the first 2 cabs and so accommodate them into 3rd cab and the remaining seats are 3.

Group 1 – 3 students - Since there enough seats in the 3rd cab, accommodate them into 3rd cab and the remaining seat is 0.

Group 5 – 2 students - Since there are enough seats in the 2nd cab, accommodate them into 2nd cab and the remaining seat is 0.

Group 2 – 1 student - Since there is a seat left in the 1st cab, accommodate him into 1st cab and the remaining seat is 0.

Using this First- fit decreasing method, we need 3 cabs and there are no remaining seats and hence seats are used to the optimum level .

Example 1: Kumaran is a trainee carpenter. He has to cut the following length of wood in the table given below. The available length of wood in the market is 8 ft. Help him to cut without wasting any of the woods.

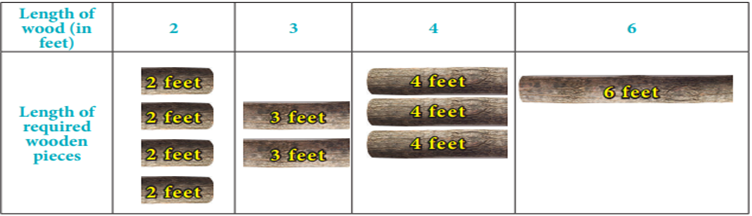
Solution:

For that, first we have to calculate minimum required.

Here, the total length of wooden pieces required = (2ft × 4 ) + (3ft × 2) + (4ft × 3) + (6ft × 1) = 8 + 6 + 12 + 6 = 32 feet

Available length of wood = 8 feet

Therefore, minimum required wood = 32 ÷ 8 = 4

So, kumaran needs 4 pieces of woods to fullfil his requirement. Let us check, how can Kumaran cut exactly four-piece of woods with no wastage using the first-fit decreasing method of packing. The following picture shows how Kumaran could cut the length of wood without any wastage.