SET LANGUAGE

INTRODUCTION:

In our daily life, we often deal with collection of objects like books, stamps, coins, etc. Set language is a mathematical way of representing a collection of objects.

represents a collection of fruits and represents a collection of house- hold items.

SET :

A set is a well-defined collection of objects.

Here “well-defined collection of objects” means that given a specific object it must be possible for us to decide whether the object is an element of the given collection or not.

The objects of a set are called its members or elements.

For example,

The collection of all books in a District Central Library.

The collection of all colours in a rainbow.

The collection of prime numbers.

We see that in the adjacent box, statements (1), (2), and (4) are well defined and therefore they are sets. Whereas (3) and (5) are not well defined because the words good and beautiful are difficult to agree on. I might consider a student to be good and you may not. I might consider Malligai is beautiful but you may not. So we will consider only those collections to be sets where there is no such ambiguity.

Therefore (3) and (5) are not sets.

NOTATION

A set is usually denoted by capital letters of the English Alphabets A, B, P, Q, X, Y, etc.

The elements of a set are denoted by small letters of the English alphabets a, b, p, q, x, y, etc.

The elements of a set is written within curly brackets “{ }”

If x is an element of a set A or x belongs to A, we write x ∈ A.

If x is not an element of a set A or x does not belongs to A, we write x ∉ A.

For example,

Consider the set A = {2,3,5,7} then

2 is an element of A; we write 2∈A

is an element of A; we write 5∈A

is not an element of A; we write 6∉A

Example 1.1

Consider the set A = {Ashwin, Muralivijay, Vijay Shankar, Badrinath }.

Fill in the blanks with the appropriate symbol ∈ or ∉.

(i) Muralivijay ____ A. (ii) Ashwin ______ A. (iii) Badrinath ______A.

(iv) Ganguly _____ A. (v) Tendulkar _____ A.

Solution

(i) Muralivijay ∈ A. (ii) Ashwin ∈ A (iii) Badrinath ∈ A (iv) Ganguly ∉ A. (v) Tendulkar ∉ A.

REPRESENTATION OF A SET:

The collection of odd numbers can be described in many ways:

“The set of odd numbers” is a fine description, we understand it well.

It can be written as {1, 3, 5, …} and you know what I mean.

Also, it can be said as the collection of all numbers x where x is an odd number.

All of them are equivalent and useful. For instance,the two descriptions “The collection of all solutions to the equation x–5 = 3” and {8} refer to the same set.

A set can be represented in any one of the following three ways or forms:

Descriptive Form.

Set-Builder Form or Rule Form.

Roster Form or Tabular Form.

1. Descriptive Form

In descriptive form, a set is described in words.

For example,

(i) The set of all vowels in English alphabets.

(ii)The set of whole numbers.

2. Set Builder Form or Rule Form

In set builder form, all the elements are described by a rule.

For example,

(i) A = {x : x is a vowel in English alphabets}

(ii) B = {x|x is a whole number}

3. Roster Form or Tabular Form

A set can be described by listing all the elements of the set.

For example,

(i) A = {a, e, i, o, u}

(ii) B = {0,1,2,3,…}

Example :

Write the set of letters of the following words in Roster form

(i) ASSESSMENT (ii) PRINCIPAL

Solution

(i) ASSESSMENT

A= {A, S, E, M, N, T}

(ii) PRINCIPAL

B={P, R, I, N, C, A, L}

TYPES OF SETS

There is a very special set of great interest: the empty collection ! Why should one care about the empty collection? Consider the set of solutions to the equation x²+1 = 0. It has no elements at all in the set of Real Numbers. Also consider all rectangles with one angle greater than 90 degrees. There is no such rectangle and hence this describes an empty set.

So, the empty set is important, interesting and deserves a special symbol too.

1. Empty Set or Null Set

A set consisting of no element is called the empty set or null set or void set.

Empty Set or Null Set Q ` Q

A set consisting of no element is called the empty set or null set or void set.

It is denoted by ! or { }.

For example,

(i) A={x : x is an odd integer and divisible by 2}

NA={ } or

(ii) The set of all integers between 1 and 2.

2. Singleton Set

A set which has only one element is called a singleton set.

For example,

(i) A = {x : 3 < x < 5, x } (ii) The set of all even prime numbers.

3 Finite Set

A set with finite number of elements is called a finite set.

It is denoted by Ø or { }.

For example,

(i) A={x : x is an odd integer and divisible by 2}

A={ } or Ø

(ii) The set of all integers between 1 and 2.

For example,

The set of family members.

The set of indoor/outdoor games you play.

The set of curricular subjects you learn in school.

A = {x : x is a factor of 36}

4. Infinite Set

A set which is not finite is called an infinite set.

For example,

(i) {5,10,15,...}

(ii) The set of all points on a line.

To discuss further about the types of sets, we need to know the cardinality of sets.

CARDINAL NUMBER OF A SET :

When a set is finite, it is very useful to know how many elements it has. The number of elements in a set is called the Cardinal number of the set.

The cardinal number of a set A is denoted by n(A)

Example 1.3

If A = {1,2,3,4,5,7,9,11}, find n(A).

Solution

A = {1,2,3,4,5,7,9,11}

Since set A contains 8 elements, n(A) = 8.

5. Equivalent Sets

Two finite sets A and B are said to be equivalent if they contain the same number of elements. It is written as A ≈ B.

If A and B are equivalent sets, then n(A) = n(B)

Consider A = { ball, bat} and B = {history, geography}.

Here A is equivalent to B because n(A) = n(B) = 2.

Example 1.4

Are P = { x : –3 ≤ x ≤ 0, x ∈ Z} and Q = The set of all prime factors of 210, equivalent sets?

Solution

P = {–3, –2, –1, 0}, The prime factors of 210 are 2,3,5,and 7 and so, Q = {2, 3, 5, 7} n(P) =4 and n(Q) = 4. Therefore P and Q are equivalent sets.

6. Equal Sets

Two sets are said to be equal if they contain exactly the same elements, otherwise they are said to be unequal.

In other words, two sets A and B are said to be equal, if

every element of A is also an element of B

every element of B is also an element of A

For example,

Consider the sets A = {1, 2, 3, 4}  and B = {4, 2, 3, 1}

Since A and B contain exactly the same elements, A and B are equal sets.

A set does not change, if one or more elements of the set are repeated.

For example, if we are given

A={a, b, c} and B={a, a, b, b, b, c} then, we write B = { a, b, c, }. Since, every element of A is also an element of B and every element of B is also an element of A, the sets A and B are equal.

Example 1.5

Are A = {x : x ∈ N, 4 ≤ x ≤ 8} and

B = { 4, 5, 6, 7, 8} equal sets?

Solution

A = { 4, 5, 6, 7, 8}, B = { 4, 5, 6, 7, 8}

A and B are equal sets.

SUBSET

Let A and B be two sets. If every element of A is also an element of B, then A is called a subset of B. We write A ⊆ B.

A ⊆ B is read as “A is a subset of B”

Thus A ⊆ B, if a ⊆ A implies a ⊆ B.

If A is not a subset of B, we write A ⊈ B

Clearly, if A is a subset of B, then n(A) ≤ n(B).

Since every element of A is also an element of B, the set B must have at least as many elements as A, thus n(A) ≤ n(B).

The other way is also true. Suppose that n(A) > n(B), then A has more elements than B, and hence there is at least one element in A that cannot be in B, so A is not a subset of B.

For example,

(i) {1} ⊆ {1,2,3}  (ii) {2,4} ⊈{1,2,3}

Example1.6

Write all the subsets of A = {a, b}.

Solution

A= {a,b}

Subsets of A are Ø,{a}, {b} and {a, b}.

 Power Set

The fun begins when we realise that elements of sets can themselves be sets !

That is not very difficult to imagine: the people in school form a set, that consists of the set of students, the set of teachers, and the set of other staff. The set of students then has many sets as its elements: the set of students in class 1, the set of class 2 children, and so on. So we can easily talk of sets of sets of sets of …. of sets of elements !

The set of all subsets of a set A is called the power set of ‘A’. It is denoted by P(A).

For example,

(i) If A={2, 3}, then find the power set of A.

 The subsets of A are Ø , {2},{3},{2,3}.

 The power set of A,

P(A) = {Ø ,{2},{3},{2,3}}

(ii) If A = {Ø , {Ø}}, then the power set of A is { Ø , {Ø , {Ø}}, {Ø} , {{Ø}} }.

Example:

Find the number of subsets and the number of proper subsets of a set X={a, b, c, x, y, z}.

Solution

Given X={a, b, c, x, y, z}.Then, n(X) =6

The number of subsets = n[P(X)] = 2⁶ = 64

The number of proper subsets = n[P(X)]-1 = 2⁶–1

 = 64 – 1 = 63

SET OPERATIONS

We started with numbers and very soon we learned arithmetical operations on them. In algebra we learnt expressions and soon started adding and multiplying them as well, writing (x²+2) (x-3) etc. Now that we know sets, the natural question is, what can we do with sets, what are natural operations on them ?

What can we do with sets ? We can pick an element. But then which element ? There are many in general, and hence “picking an element” is not an operation on a set. But like we did with addition, subtraction etc, we can try and think of operations that combine two given sets to get a new set. 

COMPLEMENT OF A SET

The Complement of a set A is the set of all elements of U (the universal set) that are not in A.

It is denoted by A′ or A^c. In symbols A′= {x : x∈U, x∉A}

VENN DIAGRAM FOR COMPLEMENT OF A SET :

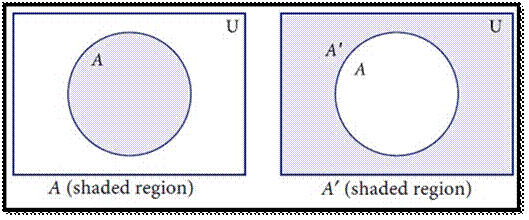
For example,

If U = {all boys in a class} and A= {boys who play Cricket}, then complement of the set A is A′= {boys who do not play Cricket}.

Example:

If U = {c, d, e, f, g, h, i, j} and A = { c, d, g, j} , find A′.

Solution

U = {c, d, e, f, g, h, i, j}, A = {c, d, g, j}

A′ ={e, f, h, i}

UNION OF TWO SETS

The union of two sets A and B is the set of all elements which are either in A or in B or in both. It is denoted by A∪B and read as A union B.

In symbol, A∪B = {x : x ∈A or x∈B}

The union of two sets can be represented by Venn diagram as given below

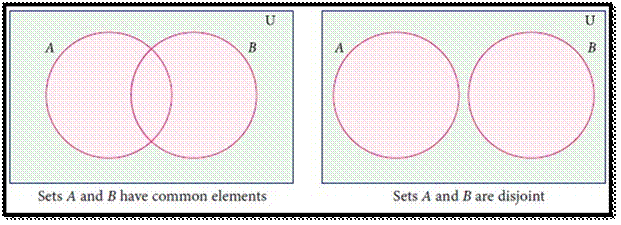
For example,

If P ={Asia,Africa, Antarctica, Australia} and Q = {Europe, North America, South America}, then the union set of P and Q is P∪Q = {Asia, Africa, Antartica, Australia, Europe, North America, South America}.

Example :

If A={1, 2, 6} and B={2, 3, 4} , find A∪B.

Solution

Given A={1, 2, 6}, B={2, 3, 4}

A∪B={1, 2, 3, 4,6}.

INTERSECTION OF TWO SETS

The intersection of two sets A and B is the set of all elements common to both A and B. It is denoted by A∩B and read as A intersection B.

In symbol , A∩B={x : x∈A and x∈B}

Intersection of two sets can be represented by a Venn diagram as given below

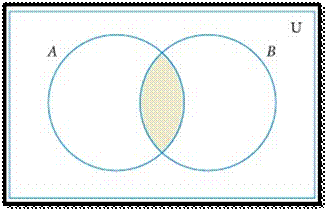
For example,

If A = {1, 2, 6}; B = {2, 3, 4}, then A∩B = {2} because 2 is common element of the sets A and B.

Example :

Let A = {x : x is an even natural number and 1< x ≤ 12} and

B = { x : x is a multiple of 3, x ∈ N and x≤12} be two sets. Find A∩B.

Solution

Here A = {2, 4, 6, 8, 10, 12} and B = {3, 6, 9, 12}

A∩B = {6, 12}

Example:

If A = {2, 3} and C = { }, find A∩C.

Solution

There is no common element and hence A∩C ={ }

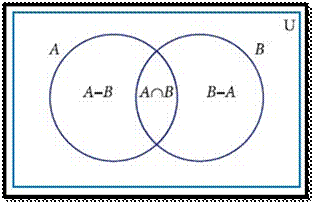
DIFFERENCE OF TWO SETS

Let A and B be two sets, the difference of sets A and B is the set of all elements which are in A, but not in B. It is denoted by A–B or A\B and read as A difference B.

In symbol, A–B = { x : x ∈ A and x ∉ B}

B–A = { y : y ∈ B and y ∉ A}.

Venn diagram for set difference

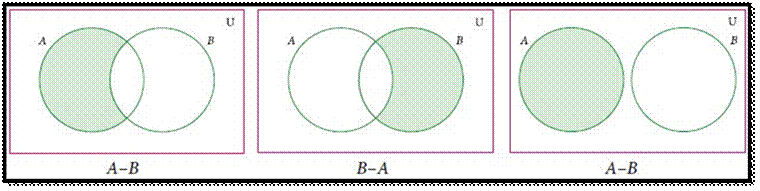
Example:

If A={–3, –2, 1, 4} and B= {0, 1, 2, 4}, find (i) A–B (ii) B–A.

Solution

A–B ={–3, -2, 1, 4} – {0, 1, 2, 4} = { -3, -2}

B–A = {0, 1, 2, 4} –{–3, -2, 1, 4} = { 0, 2}

 SYMMETRIC DIFFERENCE OF SETS

The symmetric difference of two sets A and B is the set (A–B)∪(B–A). It is denoted by AΔB.

A  B={ x : x ∈ A–B or x ∈ B–A}

Example:

If A = {6, 7, 8, 9} and B={8, 10, 12}, find AΔB.

Solution

A–B = {6, 7, 9}

B–A = {10, 12}

AΔB = (A–B)∪(B–A) = {6, 7, 9}∪{10,12}

AΔB = {6, 7, 9, 10, 12}.

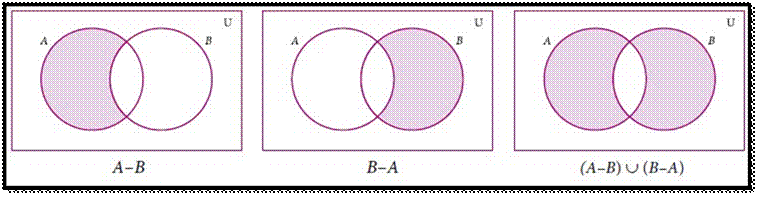
Example 1.16

Represent AΔB through Venn diagram.

Solution

AΔB= (A–B) ∪ (B–A)

PROPERTIES OF SET OPERATIONS

It is an interesting investigation to find out if operations among sets (like union, intersection, etc) follow mathematical properties such as Commutativity, Associativity, etc., We have seen numbers having many of these properties;

De Morgon’s Law :

De Morgon’s Law states that the complement of the union of two sets is the intersection of their complements and the complement of the intersection of two sets is the union of their complements. These are mentioned after the great mathematician De Morgan. This law can be expressed as ( A ∪ B) ‘ = A ‘ ∩ B ‘. In set theory, these laws relate the intersection and union of sets by complements.

De morgan's law for set difference :

Example 1 :

Let A  =  { a, b, c, d, e, f, g, x, y, z }, B  =  { 1, 2, c, d, e } and C  =  { d, e, f, g, 2, y }. Verify De Morgan’s laws of set difference.

Solution :

First, we shall verify A \ (B u C)  =  (A \ B) n (A \ C)

To do this, we consider

B u C  =  { 1, 2, c, d, e } u { d, e, f, g, 2, y }

B u C  =  { 1, 2, c, d, e, f, g, y }

We know that

A/(B u C) =  {a, b, c, d, e, f, g, x, y, z}\{1, 2, c, d, e, f, g, y}

A / (B u C)  =  { a, b, x, z } ---------(1)

A \ B   =  { a, b, f, g, x, y, z }

A \ C   =  { a, b, c, x, z }

(A \ B) n (A \ C)  =  { a, b, x, z } ---------(2)

From (1) and (2), it is clear that A\(B u C)  =  (A\B)n(A\C)

Example 2 :

Let A = {10,15, 20, 25, 30, 35, 40, 45, 50}, B = {1, 5,10,15, 20, 30} and C = {7, 8,15,20,35,45, 48}. Verify A \(B n C) = (A \ B) U (A \ C).

Solution :

First, we shall verify A \ (B u C)  =  (A \ B) n (A \ C)

To do this, we consider

B u C  = {1, 5, 10, 15, 20, 30} U {7, 8, 15, 20, 35, 45, 48}

B u C  =  { 1, 5, 7, 8, 10, 15 , 20,30, 35, 45, 48 }

We know that

A \ (B u C) =  {10,15, 20, 25, 30, 35, 40, 45, 50}\{ 1, 5, 7, 8, 10, 15 , 20,30, 35, 45, 48 }

A / (B u C)  =  { 25, 40, 50 } ---------(1)

A\B = {10, 15, 20, 25, 30, 35, 40, 45, 50}\{1, 5, 10, 15, 20, 30}

  =  {25, 35, 40, 45, 50}

A\C = {10, 15, 20, 25, 30, 35, 40, 45, 50}\ {7, 8, 15, 20, 35, 45, 48}

  =  {25, 30, 40, 50}

(A\B) U (A\C) = { 25, 40, 50} ---------(2)

From (1) and (2), it is clear that A\(B n C)  =  (A\B)u(A\C)

After having gone through the stuff given above, we hope that the students would have understood "De morgans law for set difference". 

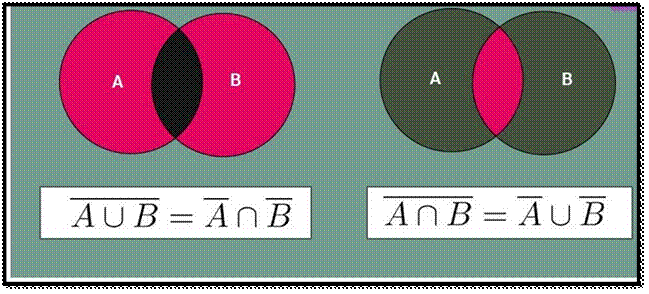
DE MORGAN’S LAWS FOR COMPLEMENTATION:

De Morgan’s law states that ‘The complement of the union of two sets A and B is equal to the intersection of the complement of the sets A’ and B’. Also according to De Morgan’s law, the complement of the intersection of two sets A and B is equal to the union of the complement of the sets A and B i.e.,

(A∪B)’ = A’ ∩ B’

COMPLEMENT LAWS:

 The union of a set A and its complement A’ gives the universal set U of which A and A’ are a subset.

A ∪ A’ = U

Also the intersection of a set A and its complement A’ gives the empty set ∅.

A ∩ A’ = ∅

For Example: If U = {1 , 2 , 3 , 4 , 5 } and A = {1 , 2 , 3 } then A’ = {4 , 5}. From this it can be seen that

A ∪ A’ = U = { 1 , 2 , 3 , 4 , 5}

Also

A ∩ A’ = ∅

Example: 

A universal set U which consists of all the natural numbers which are multiples of 3, less than or equal to 20. Let A be a subset of U which consists of all the even numbers and the set B is also a subset of U consisting of all the prime numbers. Verify De Morgan Law.

Solution:

 We have to verify (A ∪ B)’ = A’ ∩ B’ and (A ∩ B)’ = A’∪B’. Given that,

U = {3 , 6 , 9 , 12 , 15 , 18}

A = {6 , 12 , 18}

B = {3}

The union of both A and B can be given as,

A ∪ B = {3 , 6 , 12 , 18}

The complement of this union is given by,

(A ∪ B)’={9 , 15}

Also the intersection and its complement is given by:

A ∩ B = ∅

(A ∩ B)’ = {3 , 6 , 9 , 12 , 15 ,18}

Now, the complement of the sets A and B can be given as:

A’ = {3 , 9 , 15}

B’ = {6 , 9 , 12 , 15 , 18}

Taking the union of both these sets, we get,

A’∪B’ = {3 , 6 , 9 , 12 , 15 ,18}

And the intersection of the complemented sets is given as,

A’ ∩ B’ = {9 , 15}

We can see that:

(A ∪ B)’ = A’ ∩ B’ = {9 , 15}

And also,

(A ∩ B)’ = A’ ∪ B’ = {3 , 6 , 9 , 12 , 15 ,18}

Hence the above result is true in general and is known as De Morgan Law.

Application on Cardinality of Sets:

We have learnt about the union, intersection, complement and difference of sets.

Now we will go through some practical problems on sets related to everyday life.

If A and B are two finite sets, then

n(A∪B) = n(A)+n(B) – n(A∩B)

(i) n(A∪B) = n(A)+n(B)– n(A∩B)

(ii) n(A–B) = n(A) – n(A∩B)

(iii) n(B–A) = n(B)– n(A∩B)

(iv) n(A′) = n(U) – n(A)

EXAMPLE 1:

From the Venn diagram, verify that

n(A∪B) = n(A)+n(B) – n(A∩B)

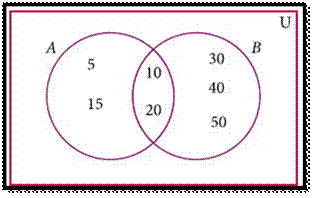
Solution

From the venn diagram,

 A = {5, 10, 15, 20}

 B = {10, 20, 30, 40, 50,}

Then A∪B = {5, 10, 15, 20, 30, 40, 50}

A∩B = {10, 20}

n(A) = 4, n(B) = 5, n(A∪B) = 7, n(A∩B) = 2

n(A∪B) = 7   ----- (1)

n(A)+n(B)–n(A∩B) = 4+5–2

 =7    ----- (2)

From (1) and (2), n(A∪B) = n(A)+n(B)–n(A∩B).

EXAMPLE 2:

If n(A) = 36, n(B) = 10, n(A∪B)=40, and n(A′)=27 find n(U) and n(A∩B).

Solution

n(A) = 36, n(B) =10, n(A∪B)=40, n(A′)=27

(i) n(U) = n(A)+n(A′) = 36+27 = 63

(ii) n(A∩B) = n(A)+n(B)–n(A∪B) = 36+10-40 = 46-40 = 6

EXAMPLE 3:

Let A={b, d, e, g, h} and B = {a, e, c, h}. Verify that n(A–B) = n(A)–n(A∩B).

Solution

A = {b, d, e, g, h}, B = {a, e, c, h}

 A – B = {b, d, g}

n(A–B) = 3                 ... (1)

 A ∩ B = {e, h}

n(A ∩ B) = 2 , n(A) = 5

n(A) – n(A∩B) = 5-2

 = 3                   ... (2)

Form (1) and (2) we get n(A–B) = n(A)–n(A∩B).

EXAMPLE 4:

In a school, all students play either Hockey or Cricket or both. 300 play Hockey, 250 play Cricket and 110 play both games. Find

1.        the number of students who play only Hockey.

2.        the number of students who play only Cricket.

3.        the total number of students in the School.

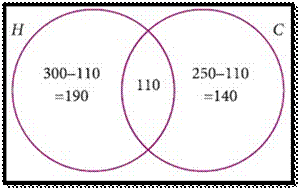
Solution:

Let H be the set of all students play Hockey and C be the set of all students play Cricket.

Then n(H) = 300, n(C) = 250 and n(H ∩ C) = 110

Using Venn diagram,

From the Venn diagram,

(i) The number of students who play only Hockey = 190

(ii) The number of students who play only Cricket = 140

(iii) The total number of students in the school = 190+110+140 =440

EXAMPLE 4:

In a party of 60 people, 35 had Vanilla ice cream, 30 had Chocolate ice cream. All the people had at least one ice cream. Then how many of them had,

1.        both Vanilla and Chocolate ice cream.

2.        only Vanilla ice cream.

3.        only Chocolate ice cream.

Solution :

Let V be the set of people who had Vanilla ice cream and C be the set of people who had Chocolate ice cream.

Then n(V) = 35, n(C) = 30, n(V∪C) = 60,

Let x be the number of people who had both ice creams.

From the Venn diagram

 35 – x + x +30 – x = 60

 65 – x = 60

 x= 5

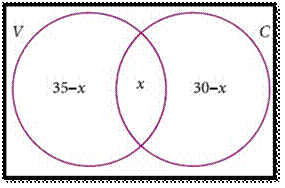
Hence 5 people had both ice creams.

(i) Number of people who had only Vanilla ice cream = 35 – x

 = 35– 5 = 30

(ii) Number of people who had only Chocolate ice cream = 30 – x

 = 30 – 5 = 25