REAL NUMBERS

INTRODUCTION:

Numbers, numbers, everywhere!

Do you have a phone at home? How many digits does its dial have?

What is the Pin code of your locality? How is it useful?

When you park a vehicle, do you get a ‘token’? What is its purpose?

Have you handled 24 ‘carat’ gold? How do you decide its purity?

How high is the ‘power’ of your spectacles?

How much water does the overhead tank in your house can hold?

Does your friend have fever? What is his body temperature?

You have learnt about many types of numbers so far. Now is the time to extend the ideas further.

RATIONAL NUMBERS:

When you want to count the number of books in your cupboard, you start with 1, 2, 3, … and so on. These counting numbers 1, 2, 3, … , are called Natural numbers. You know to show these numbers on a line (see Fig. 2.1).

We use N to denote the set of all natural numbers.

N= { 1, 2, 3, … }

Suppose there are 5 books in your cupboard and you remove them one by one; the number of books diminish step by step. You remove one, it becomes 4, remove one more, it becomes 3, again one more is removed leaving 2, once again remove one and you are left with 1. If this last one is also taken out, the cupboard is empty (since no books are there). To denote such a situation we use the symbol 0. It denotes absence of any quantity. Thus to say “there are no books”, you can write “the number of books is zero”. Including zero as a digit you can now consider the numbers 0, 1, 2, 3, … and call them Whole numbers. With this additional entity, the number line will look as shown below

We use W to denote the set of all Whole numbers.

W= { 0, 1, 2, 3, … }

Certain conventions lead to more varieties of numbers. Let us agree that certain conventions may be thought of as “positive” denoted by a ‘+’ sign. A thing that is ‘up’ or ‘forward’ or ‘more’ or ‘increasing’ is positive; and anything that is ‘down’ or ‘backward’ or ‘less’ or ‘decreasing’ is “negative” denoted by a ‘–’ sign.

For example, if I make a profit of Rs.1000 in my business, I would call that +1000, and if I lose Rs. 5000, that would be -5000. Why? Similarly, if a mountain’s base is 2 km below sea level and its peak is 3 km above sea level, then the altitude of its base is –2 and the altitude of its peak is +3. (What is its total height? Is it 5 km?).

With this understanding, you can treat natural numbers as positive numbers and rename them as positive integers; thereby you have enabled the entry of negative integers –1, –2, –3, … .

Note that –2 is “more negative” than –1. Therefore, among –1 and –2, you find that –2 is smaller and –1 is bigger. Are –2 and –1 smaller or greater than –3? Think about it.

The number line at this stage may be given as follows:

We use Z to denote the set of all Integers.

Z= { …, –3, –2, –1, 0, 1, 2, 3, … }.

Draw a copy of Fig 2.2. Hold your whole number line up to a mirror on zero. You will see the natural numbers reflected in the mirror. The reflected numbers attached with a minus sign are negative integers. So the numbers to the left of 0 are negative, and the numbers to the right of 0 are positive. But 0 is neither negative nor positive; 0 is just 0. It’s non-committal!

When you look at the figures (Fig. 2.2 and 2.3) above, you are sure to get amused by the gap between any pair of consecutive integers. Could there be some numbers in between?

How did you actually draw the number line N (Fig. 2.1) initially? Draw any line, mark a point 1 on it. From 1, choose another point on its right side at a preferred ‘unit’ distance and call it 2. Repeat this as many times as you desire. To get W (Fig. 2.2), from 1, go one unit on the left to get 0. Now Z is easier; just repeat the exercise on the left side.

You have come across fractions already. How will you mark the point that shows 1/2 on Z? It is just midway between 0 and 1. In the same way, you can plot 1/3, 1/4, 1/5,2 3/4.... etc. You may find that many different fractions are shown by the same point. Can you say ‘why’? Will 5/4 and 10/8 be represented by the same point? Do you think 7/9 and 35/55 represent the same point? You will now easily visualize similar fractions on the left side of zero. These are all fractions of the form a/b  where a and b are integers with one restriction that b ≠ 0. (Why?) If a fraction is in decimal form, even then the setting is same.

Because of the connection between fractions and ratios of lengths, we name them as Rational numbers. Here is a rough picture of the situation:

Since a fraction can have many equivalent fractions , there are many possible names for the same rational number. Thus 1/3, 2/6, 8/24 8 all these denote the same rational number.

Example :

Find any two rational numbers between 1/2 and 2/3.

Solution 1

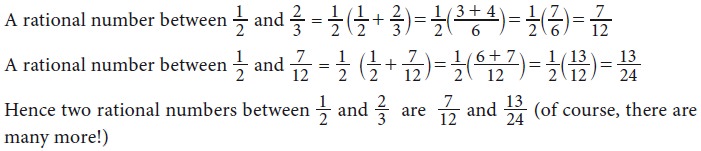
There is an interesting result that could help you to write instantly rational numbers between any two given rational numbers.

Solution 2

21 < 32 gives or 21 2 3 1 2 32 21 53 32 < < < < ++ gives or 2 1 2 5 1 3 53 5 3 3 2 32 21 74 53 85 32 < < < < < < < 1 ++ ++

Solution 3

Any more new methods to solve? Yes, if decimals are your favourites, then the above example can be given an alternate solution as follows:

21 = 0.5 and 32 = 0.66...

Hence rational numbers between 21 and 32 can be listed as 0.51, 0.57,0.58,…

Solution 4

There is one more way to solve some problems. For example, to find four rational numbers between 94 and 5 3 , note that the LCM of 9 and 5 is 45; so we can write 94 = 45 20 and 53 = 45 27 .

Therefore, four rational numbers between 94 and 5 3 are , , , , 45 21 45 22 45 23 45 24 ...

IRRATIONAL NUMBERS

You saw that each rational number is assigned to a point on the number line and learnt about the denseness property of the rational numbers.  Does that mean the line is entirely filled with the rational numbers and there are no more numbers on the number line? Let us explore.

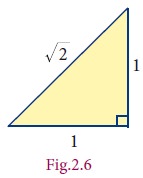
Consider an isosceles right-angled triangle whose legs are each 1 unit long.  Using Pythagoras theorem, the hypotenuse can be seen having a length √(1²+1²) (see Fig. 2.6 ). Greeks found that this √2 is neither a whole number nor an ordinary fraction. The belief of relationship between points on the number line and all numbers was shattered! √2 was called an irrational number.

An irrational number is a number that cannot be expressed as an ordinary ratio of two integers.

A natural question is how one knows that √2 is irrational. It is not difficult to justify it.

If √2 is really rational, let it be equal to p/q where p, q are integers without any common factors (so that p/q will be in its simplest form) and q ≠ 0.

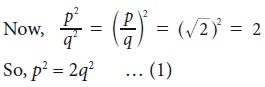
which means p² is even … (2)

As a result, p is even. …. (3)

(Can you prove this?)

Let p = 2m (How?); you get p² = 4m² ;

This, because of (1)

=> 2q² = 4m² or q²=2m².

As a result q is even ` … (4).

(3) and (4) show that p and q have a common factor 2.

This contradicts our assumption that p and q have no common factors and hence  our assumption that √2 can be written as p/q is wrong. That is, √2 is not rational.

. IRRATIONAL NUMBERS ON THE NUMBER LINE

Where are the points on the number line that correspond to the irrational numbers?

As an example, let us locate √2 on the number line. This is easy.

Remember that √2 is the length of the diagonal of the square whose side is 1 unit  (How?)Simply construct a square and transfer the length of one of its diagonals to our number line.

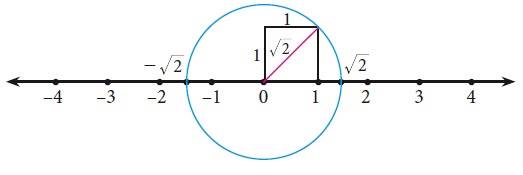
We draw a circle with centre at 0 on the number line,with a radius equal to that of diagonal of the square. This circle cuts the number line in two points, locating √2 on the right of 0 and -√2 on its left. (You wanted to locate √2 ; you have also got a bonus in -√2 )

You started with Natural numbers and extended it to rational numbers and then irrational numbers. You may wonder if further extension on the number line waits for us. Fortunately it stops and you can learn about it in higher classes.

Representation of a Rational number as terminating and non terminating decimal helps us to understand irrational numbers. Let us see the decimal expansion of rational numbers.

 DECIMAL REPRESENTATION OF A RATIONAL NUMBER

If you have a rational number written as a fraction, you get the decimal representation by long division. Study the following examples where the remainder is 0 always:

Consider the examples,

PERIOD OF DECIMAL

In the decimal expansion of the rational numbers, the number of repeating decimals is called the length of the period of decimals.

For example,

Example:

4. CONVERSION OF TERMINATING DECIMALS INTO RATIONAL NUMBERS :

Let us now try to convert a terminating decimal, say 2.945 as rational number in the fraction form.

That is, in any decimal number, each digit after the decimal point is a fraction with a denominator in increasing powers of 10. Thus,

Example:

Convert the following decimal numbers in the form of p/q , where p and q are integers and q ≠ 0: (i) 0.35 (ii) 2.176 (iii) – 0.0028

Solution

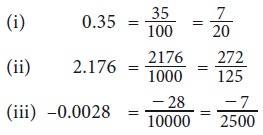
Example:

Without actual division, classify the decimal expansion of the following numbers as terminating or non – terminating and recurring.

 DECIMAL REPRESENTATION TO IDENTIFY IRRATIONAL NUMBERS

It can be shown that irrational numbers, when expressed as decimal numbers, do not terminate, nor do they repeat. For example, the decimal representation of the number π starts with 3.14159265358979, but no finite number of digits can represent π exactly, nor does it repeat.

Consider the following decimal expansions:

0.1011001110001111…

3.012012120121212…

12.230223300222333000…

√2 = 1.4142135624…

Are the above numbers terminating (or) recurring and non- terminating? No… They are neither terminating, nor non–terminating and recurring. Hence they are not rational numbers. They cannot be written in the form of p/q, where p,q, ∈ Z and q≠0. They are irrational numbers.

Example :

Find any 4 irrational numbers between 1/4 and 1/3.

Example:

Find any 3 irrational numbers between 0.12 and 0.13 .

Solution

Three irrational numbers between 0.12 and 0.13 are 0.12010010001…, 0.12040040004…, 0.12070070007…

Example:

Give any two rational numbers lying between 0.5151151115…. and 0.5353353335…

Solution

Two rational numbers between the given two irrational numbers are 0.5152 and 0.5352

Real Numbers

The real numbers consist of all the rational numbers and all the irrational numbers.

Real numbers can be thought of as points on an infinitely long number line called the real line, where the points corresponding to integers are equally spaced.

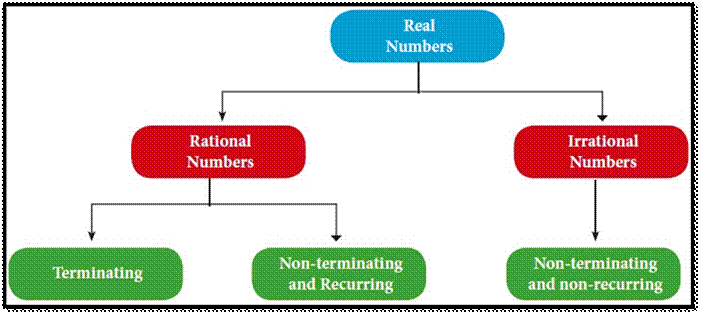
Any real number can be determined by a possibly infinite decimal representation, (as we have already seen decimal representation of the rational numbers and the irrational numbers).

Example:

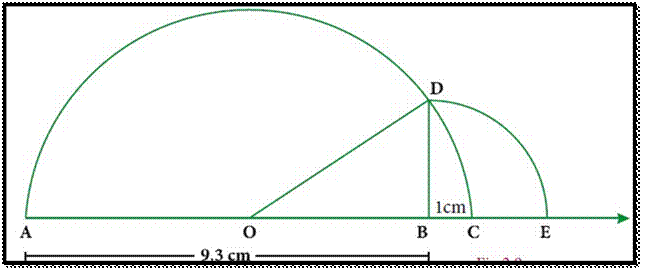
Represent √9.3 on a number line.

Solution

Draw a line and mark a point A on it.

Mark a point B such that AB = 9.3 cm.

Mark a point C on this line such that BC = 1 unit.

Find the midpoint of AC by drawing perpendicular bisector of AC and let it be O

With O as center and OC = OA as radius, draw a semicircle.

Draw a line BD, which is perpendicular to AB at B.

·           Now BD = √9.3 , which can be marked in the number line as the value of BE = BD = √9.3.

 THE SQUARE ROOT OF A REAL NUMBER

You have already come across the concept of the square root of a whole number,  decimal fractions etc. While you easily compute values like √169 (which give whole number answers), you also encounter values like √5, √18 , ... etc that yield irrational solutions.

The number 25 has two square roots 5 and –5. However, when we write √25 , we always mean the positive square root 5 (and not the negative square root –5). The symbol √  denotes the positive square root only.

THE REAL NUMBER LINE

Visualisation through Successive Magnification.

We can visualise the representation of numbers on the number line, as if we glimpse through a magnifying glass.

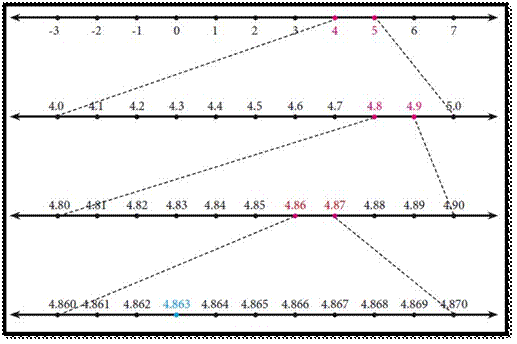
Example:

Represent 4.863 on the number line.

Solution

4.863 lies between 4 and 5(see Fig. 2.10)

Divide the distance between 4 and 5 into 10 equal intervals.

Mark the point 4.8 which is second from the left of 5 and eighth from the right of 4

4.86 lies between 4.8 and 4.9. Divide the distance into 10 equal intervals.

Mark the point 4.86 which is fourth from the left of 4.9 and sixth from the right of 4.8

4.863 lies between 4.86 and 4.87. Divide the distance into 10 equal intervals.

Mark point 4.863 which is seventh from the left of 4.87 and third from the right of 4.86.

SURDS:

Surds are the square roots  (√) of numbers which don’t simplify into a whole or rational number. It cannot be accurately represented in a fraction. In other words, a surd is a root of the whole number that has an irrational value. Consider an example, √2 ≈ 1.414213, but it is more accurate to leave it as a surd √2.

TYPES OF SURDS

The different types of surds are as follows:

• Simple Surds – A surd that has only one term is called simple surd. Example: √2, √5, …
• Pure Surds – Surds which are wholly irrational. Example: √3
• Similar Surds – The surds having the same common surds factor
• Mixed Surds – Surds that are not wholly irrational and can be expressed as a product of a rational number and an irrational number
• Compound Surds – An expression which is the addition or subtraction of two or more surds
• Binomial Surds –  A surd that is made of two other surds

SIX RULES OF SURDS

Rule 1:

a×b−−−−√=a−−√×b√

Example:

To simplify √18

18 = 9 x 2 = 3² x 2, since 9 is the greatest perfect square factor of 18.

Therefore, √18 = √3² x 2

= √3² x √2

= 3 √2

Rule 2:

ab−−√=a√b√

Example:

√12 / 121 = √12 / √121

√2² x 3 / 11

Since 4 is the perfect square of 12

√2² x √3 / 11

= 2√3 / 11

Rule 3:

ba√=ba√×a√a√=ba√a

You can rationalize the denominator by multiplying the numerator and denominator by the denominator.

Example:

Rationalise

5/√7

5/√7 = 5/√7 x √7/√7

Multiply numerator and denominator by √7

= 5√7/7

Rule 4:

ac√±bc√=(a±b)c√

Example:

To simplify,

5√6 + 4√6

5√6 + 4√6 = (5 + 4) √6

by the rule

= 9√6

Rule 5:

ca+bn√

Multiply top and bottom by a-b √n

This rule enables us to rationalise the denominator.

Example:

To Rationalise

32+2√=32+2√×2−2√2−2√=6−32√4−2 =6−32√2

Rule 6:

ca−bn√

This rule enables you to rationalise the denominator.

Multiply top and bottom by a + b√n

Example:

To Rationalise

32−2√=32−2√×2+2√2+2√=6+32√4−2 =6+32√2

How to Solve Surds:

You need to follow some rules to solve expressions that involve surds. One method is to rationalise the denominators and it’s done by ejecting the surd in the denominator. Sometimes it may be mandatory to find the greatest perfect square factor to solve surds. This is done by considering any possible factors of the value that is square rooted. For example, you need to solve for the square root of 144. 2 x 72 gives 144 and we can have a square root of 144 without a surd. Therefore we say that 144 is the greatest perfect square factor since we cannot take the square root of a bigger number that can be multiplied by another to give 144.

Surds Problems

Example 1:

Write down the conjugate of 5√3 + √2

Solution:

The conjugate of  5√3 + √2 is 5√3 – √2.

Example 2:

Rationalize the denominator: 1/[(8√11 )- (7√5)]

Solution:

Given:  1/[(8√11 )- (7√5)]

It is known that the conjugate of (8√11 )- (7√5) is (8√11 )+(7√5)

To rationalize the denominator of the given fraction, multiply the conjugate of denominator on both numerator and denominator.

=[1/[(8√11 )- (7√5)]]× [[(8√11 )+ (7√5)]/[(8√11 )+(7√5)]]

=[(8√11 )+ (7√5)]/[(8√11 )²-(7√5)²]

=[(8√11 )+ (7√5)]/[704- 245]

= [(8√11 )+ (7√5)]/459

SCIENTIFIC NOTATION :

Suppose you are told that the diameter of the Sun is 13,92,000 km and that of the Earth is 12,740 km, it would seem to be a daunting task to compare them. In contrast, if 13,92,000 is written as 1.392 ×10⁶ and 12,740 as 1.274×10⁴, one will feel comfortable. This sort of representation is known as scientific notation

· Write 124 in scientific notation.

This is not a very large number, but it will work nicely for an example. To convert this to scientific notation, I first convert the "124" to "1.24". This is not the same number as what they gave me, but (1.24)(100) = 124 is, and 100 = 10².

Then, in scientific notation, 124 is written as 1.24 × 10².

Actually, converting between "regular" notation and scientific notation is even simpler than I just showed, because all you really need to do is count decimal places. To do the conversion for the previous example, I'd count the number of decimal places I'd moved the decimal point. Since I'd moved it two places, then I'd be dealing with a power of 2 on 10. But should it be a positive or a negative power of 2? Since the original number (124) was bigger than the converted form (1.24), then the power should be positive.

· Write in decimal notation: 3.6 × 10¹²

Since the exponent on 10 is positive, I know they are looking for a LARGE number, so I'll need to move the decimal point to the right, in order to make the number LARGER. Since the exponent on 10 is "12", I'll need to move the decimal point twelve places over.

First, I'll move the decimal point twelve places over. I make little loops when I count off the places, to keep track:

Then I fill in the loops with zeroes:

In other words, the number is 3,600,000,000,000, or 3.6 trillion

Idiomatic note: "Trillion" means a thousand billion – that is, a thousand thousand million – in American parlance; the British-English term for the American "billion" would be "a milliard", so the American "trillion" (above) would be a British "thousand milliard".

Scientific notation is a way of writing very large or very small numbers. A number is written in scientific notation when a number between 1 and 10 is multiplied by a power of 10.

For example, 650,000,000 can be written in scientific notation as 6.5 ✕ 10⁸.