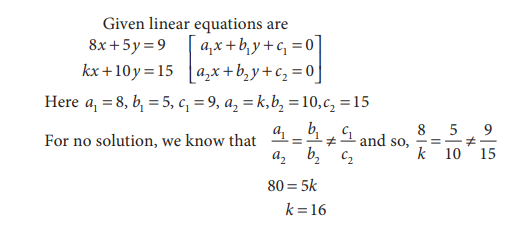ALGEBRA

Ø The part of mathematics in which letters and other general symbols are used to represent numbers and quantities in formulae and equations.

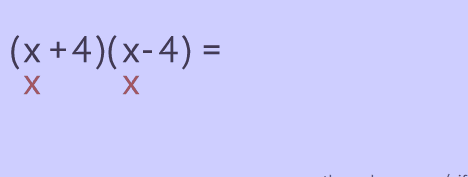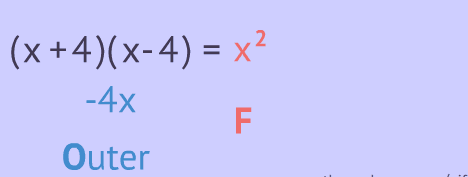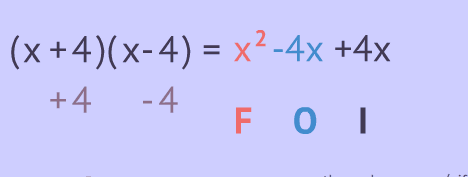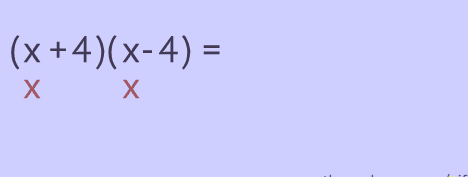
Polynomial:

Ø A polynomial is an arithmetic expression consisting of variables and constants that involves four fundamental arithmetic operations and non-negative integer exponents of variables.

Example:

= + 2a + 1

Polynomial in one variable:

Ø Polynomials in one variable are algebraic expressions that consist of terms in the form  where n is a non-negative (i.e. positive or zero) integer and aa is a real number and is called the coefficient of the term.

Ø The degree of a polynomial in one variable is the largest exponent in the polynomial.

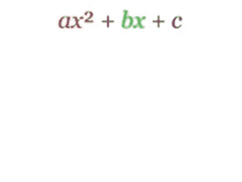
Polynomial in two variable:

Ø Polynomials in two variables are algebraic expressions consisting of terms in the form  .

Ø The degree of each term in a polynomial in two variables is the sum of the exponents in each term and the degree of the polynomial is the largest such sum.

PROBLEMS

1. Find the degree of each term for the following polynomial and also find the degree of the polynomial

Solution:

2. Find the product (4x – 5) and (  + 3x – 6).

Solution:

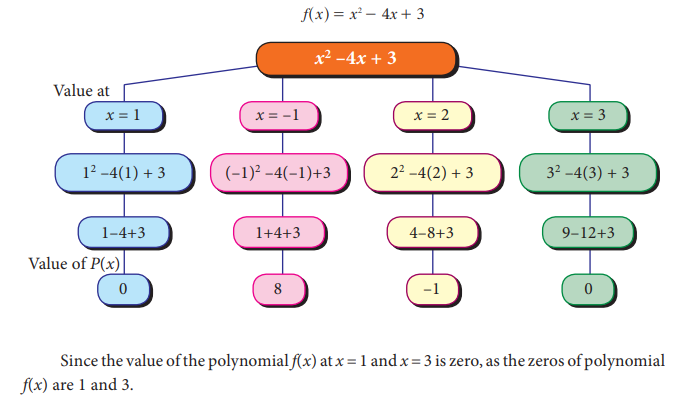
3. If f(x) = , then find the values of. Also find the zeros of the polynomial f(x).

Solution:

4. Find the Zeros of the following polynomials.

(i) f(x) = 2x + 1 (ii) f(x) = 3x – 5

Solution:

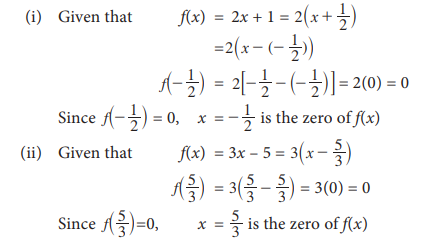
5. Find the roots of the following polynomial equations.

(i) 5x – 3 = 0 (ii) –7 –4x = 0

Solution:

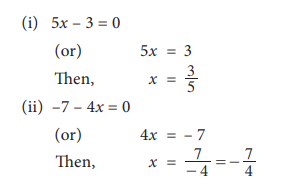
6. Check whether –3 and 3 are zeros of the polynomial – 9

Solution:

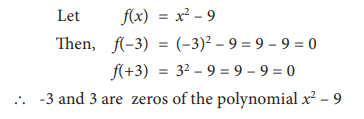
7. Without actual division , prove that f(x) = is exactly divisible by –3x + 2

Solution:

8. Show that (x + 2) is a factor of

Solution:

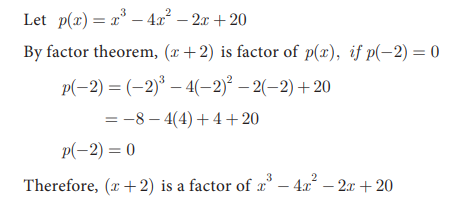
9. Find the value of m, if (x -2) is a factor of the polynomial

Solution:

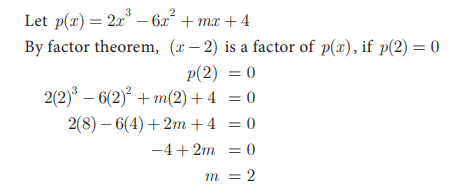
10. Expand

Solution:

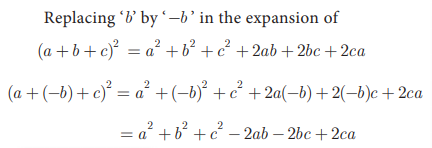
11. Factorise the following: (i) (ii) (iii) (iv)

Solution:

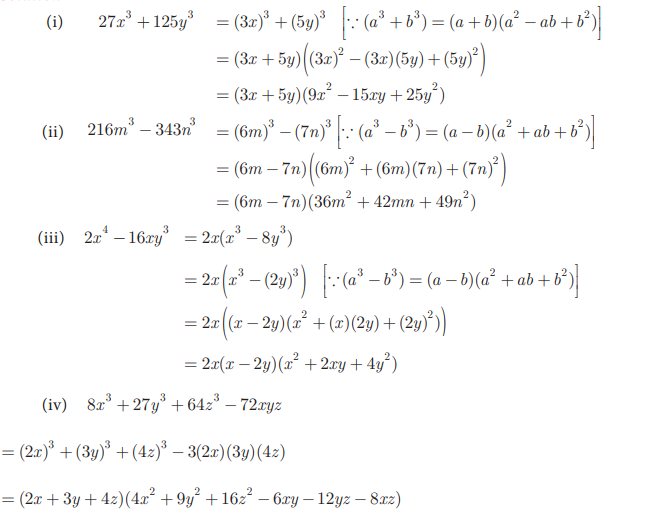
12. Factorise

Solution:

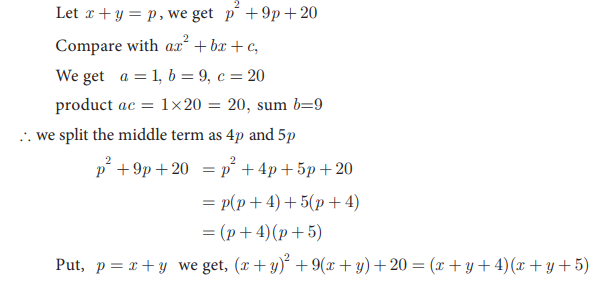
13. Find quotient and the remainder when f(x) is divided by g(x) (i) f(x) = , g(x) = 2x+1. (ii) f(x) = , g(x) =

Solution:

14. (i) Prove that ( x -1) is a factor of (ii) Prove that (x +1) is a factor of

Solution:

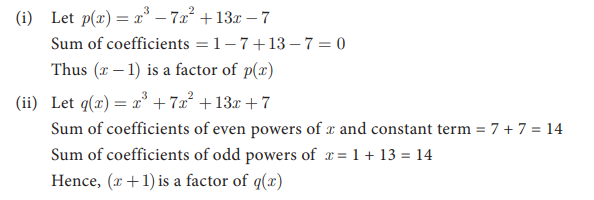
15. Given 4a + 3b = 65 and a + 2b = 35 solve by elimination method.

Solution:

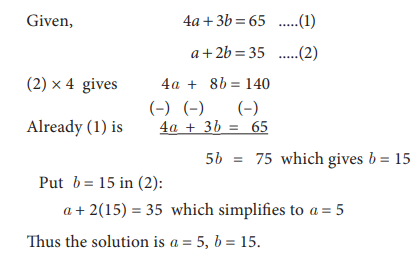
16. Solve 3x - 4y = 10 and 4x + 3y = 5 by the method of cross multiplication.

Solution:

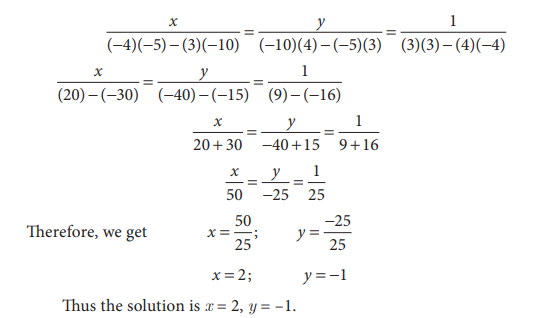
17. Solve by cross multiplication method : 3x + 5y = 21; − 7x - 6y = −49

Solution:

18. Check the value of k for which the given system of equations kx +2y = 3; 2x - 3y = 1 has a unique solution.

Solution:

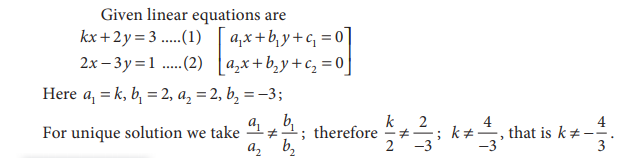
19. Find the value of k, for the following system of equation has infinitely many solutions. 2x - 3y = 7; ( k + 2)x - (2k + 1)y = 3(2k - 1 )

Solution:

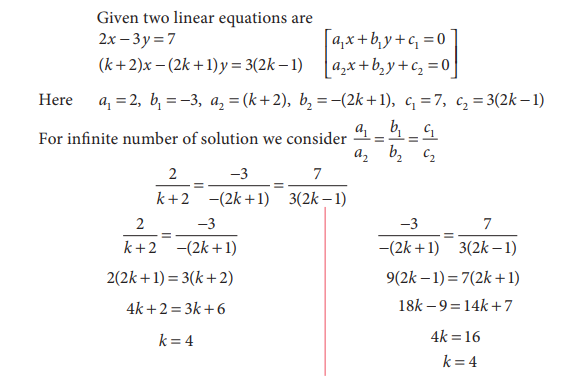
20. Find the value of k for which the system of linear equations 8x + 5y = 9; kx + 10y = 15 has no solution.

Solution: