Electromagnetic Radiation
Black
Body Radiation:
In 1900 Max Planck found an
explanation for the radiation of particle on heating a black body.
®
When a black body is heated, take for example an iron rod, it
starts becoming red and more redder as the temperature is increased. This
changes to white and then blue on further increase in temperature.
®
So, there is an increase in the frequency of radiation as
temperature increases. Therefore, a body which can emit and absorb radiation of
all frequency is called a black body.
®
And radiation emitted by such bodies is called black body
radiation. Also atoms can emit or absorb radiation only in a discontinuous
manner.
®
He named the energy emitted by such a body as quantum and the
particles quanta. The quantum
of light energy was called photon.
®
The energy (E) of a quantum of radiation is proportional to
its frequency (ν) and is expressed by equation,
E =
hν
Here,
E is quantum of energy,
ν is frequency, ![]()
h is the proportionality constant or Planck’s constant is
equal to 6.626 × ![]() J s.
J s.
Photoelectric
Effect:
Under
certain circumstances light can be used to push electrons, freeing them from
the surface of a solid. This process is called the photoelectric effect (or photoelectric
emission or photoemission), a material that can exhibit these phenomena is said
to be photo emissive, and the ejected electrons are called photoelectrons. But
these electrons are the same as others in that atom. All electrons are
identical to one another in mass, charge, spin, and magnetic moment.
Experiments to Prove Photoelectric
Effect:
In 1887, Heinrich Hertz, during
experiment with a spark-gap generator discovered the photoelectric effect of
light. A spark is generated between two small metal spheres in the transmitter
to induce a similar spark to jump between two different metal spheres in the
receiver. The air gap would often have to be smaller than a millimetre for a
receiver to consistently reproduce the spark of the transmitter. Hertz found
that he could increase the sensitivity of his spark-gap device by illuminating
it with visible or ultraviolet light.
All
forms of electromagnetic radiation transport energy and it is quite easy to imagine
this energy being used to push tiny particles of negative charge free from the
surface of a metal where they are not all that strongly confined in the first
place.
It
was Philipp Lenard (1862–1947), an assistant of Hertz, who performed the
earliest, definitive studies of the photoelectric effect. Lenard used metal
surfaces that were first cleaned and then held under a vacuum so that the
effect might be studied on the metal alone and not be affected by any surface
contaminants or oxidation. The metal sample was housed in an evacuated glass
tube with a second metal plate mounted at the opposite end. The tube was then
positioned or constrained in some manner so that light would only shine on the
first metal plate — the one made out of photo emissive material under
investigation. Such a tube is called a photocell or an electric eye. Lenard
connected his photocell to a circuit with a variable power supply, voltmeter,
and micro ammeter. He then illuminated the photo emissive surface with light of
differing frequencies and intensities.
Knocking
electrons free from the photo emissive plate would give it a slight positive
charge. Since the second plate was connected to the first by the wiring of the
circuit, it too would become positive, which would then attract the
photoelectrons floating freely through the vacuum where they would land and
return back to the plate from which they started. Keep in mind that this
experiment doesn't create electrons out of light; it just uses the energy of
the light to push electrons that are already there around the circuit. The
photoelectric current generated by this means was quite small, but could be
measured with the micro ammeter. It also serves as a measure of the rate at
which photoelectrons are leaving the surface of the photo emissive material.
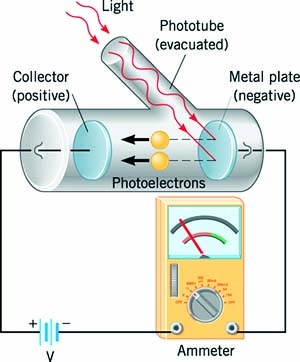
Note
how the power supply is wired into the circuit — with its negative end
connected to the plate that isn't illuminated. This sets up a potential
difference that tries to push the photoelectrons back into the photo emissive surface.
When the power supply is set to a low voltage it traps the least energetic
electrons, reducing the current through the micro ammeter. Increasing the
voltage drives increasingly more energetic electrons back until finally none of
them are able to leave the metal surface and the micro ammeter reads zero. The
potential at which this occurs is called the stopping potential. It is a
measure of the maximum kinetic energy of the electrons emitted as a result of
the photoelectric effect.
What
Lenard found was that the intensity of the incident light had no effect on the
maximum kinetic energy of the photoelectrons. Those ejected from exposure to a
very bright light had the same energy as those ejected from exposure to a very
dim light of the same frequency. In keeping with the law of conservation of
energy, however, more electrons were ejected by a bright source than a dim
source.
In 1905, Einstein realized that
light was behaving as if it was composed of tiny particles (initially called
quanta and later called photons) and that the energy of each particle was
proportional to the frequency of the electromagnetic radiation that it was a
part of. This resulted in equations which are valid for visible and ultraviolet
light.
Energy
of photon = Energy needed to remove an electron + Kinetic
energy of the emitted electron
hν = W + E
where,
h
is Planck's constant
ν
is the frequency of the incident photon
W is the work
function, which is the minimum energy required to remove an electron from the
surface of a given metal, hν0
ν0
is the threshold frequency for the photoelectric effect
E
is the maximum kinetic energy of ejected electrons, ![]() mev2
mev2
m
is the rest mass of the ejected electron
v
is the speed of the ejected electron
Therefore,
hν = hν0
+ ![]() mev2
mev2
No electron will be
emitted if the incident photon's energy is less than the work function.
From the above we
know:
® The rate at which photoelectrons are ejected is
directly proportional to the intensity of the incident light, for a given frequency
of incident radiation and metal.
® The time between the incidence and emission of a
photoelectron is very small, less than 10–9 second.
® For a given metal, there is a minimum frequency of
incident radiation below which the photoelectric effect will not occur so no
photoelectrons can be emitted (threshold frequency).
® Above the threshold frequency, the maximum kinetic
energy of the emitted photoelectron depends on the frequency of the incident
radiation but is independent of its intensity.
® If the incident light is linearly polarized then the
directional distribution of emitted electrons will peak in the direction of
polarization (the direction of the electric field).
Problems:
1. Calculate energy of
one mole of photons of radiation whose frequency is 5 × 1014 Hz.
(Avogadro’s number = 6.022 × 1023 mol−1)
Solution:
Planck’s constant h = 6.626 × 10−34
J s
Frequency v = 5 × 1014 Hz or s−1
E = hv
= 6.626 × 10−34 × 5 × 1014
Energy of a single
photon = 33.13 × 10−20 J
Energy
of one mole of photons = Energy of photon ×
Avogadro’s number
= 33.13
× 10−20 J × 6.022 × 1023 mol−1
= 199.50
× 103 J mol−1
= 199.50
kJ mol−1
2. A 100 watt bulb emits
monochromatic light of wavelength 400 nm. Calculate the number of photons
emitted per second by the bulb.
Solution:
Power of bulb = 100 watts
= 100 J s−1
E = hv
Wavelength of light λ
= 400 nm
= 400 × 10−9
m
The velocity of light c = 3.0 × 108 ms−1
Frequency ν =
![]()
= ![]()
=
7.5 × 1014
s−1
E = hv
= 6.626 × 10−34
× 7.5 × 1014
= 49.695 × 10−20 J
Energy of a single
photon = 49.695 × 10−20 J
Number of photons emitted
= ![]()
= ![]()
= 2.012 × 1020 s−1