Ideal Gas
Real time intermolecular forces and external forces which act on the gas
are not taken into consideration. All the above four relationships combine to
form an ideal gas under ideal conditions. Combining all the laws together we
get an ideal gas law.
We know from Boyle’s law
V ∝ ![]()
We know from Charles’ law
V
=
T
We know from Avogadro’s law
V
= n
From this we get,
V ∝ ![]()
V = R ![]()
pV = RnT
R = ![]() ------
(1)
------
(1)
R is called gas constant. It is same for all gases. Therefore it is also called as Universal Gas Constant. Equation (1) is called ideal gas equation. Value of R can be calculated if the other values are known. Volume of one mole of an ideal gas under standard temperature and pressure conditions (273.15 K and 1 bar pressure) is 22.710981 L mol–1. Value of R for one mole of an ideal gas can be calculated under these conditions as follows:
R = ![]()
R = 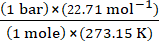
= 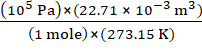
= 8.314 Pa m3 mol−1
K−1
= 8.314 J K−1 mol−1
An Ideal gas equation is a
relation between four variables and it describes the state of any gas,
therefore, it is also called equation
of state. Let us now go
back to the ideal gas equation. This is the relationship for the simultaneous
variation of the variables. If temperature, volume and pressure of a fixed
amount of gas vary from T1,
V1 and p1 to T2, V2
and p2 then we can write
R = ![]()
n R = ![]() and
and
n R = ![]()
![]() =
=
![]() ------
(2)
------
(2)
Equation (2) is a very useful equation. If out of six, values of five variables are known, the value of unknown variable can be calculated from the equation (2). This equation is also known as Combined gas law.
Problems:
At 25 ͦC and 760 mm of Hg
pressure a gas occupies 600 ml volume. What will be its pressure at a height
where temperature is 10 ͦC and
volume of the gas is 640 ml.
Solution:
We have,
T1
= 25 ͦC
= 25 + 273
= 298 K
T2
= 10 ͦC
= 10 + 273
= 283 K
V1
= 600 ml
V2
= 640 ml
p1
= 760 mm of Hg
p2
= ?
![]() =
= ![]()
![]() =
= ![]()
p2 = ![]()
p2 = 676.6 mm Hg
From the ideal gas equation (1),
R = ![]()
n = ![]()
![]() =
= ![]()
We know that,
n = ![]()
![]() =
= ![]()
Also density d = ![]()
![]() =
= ![]()
Therefore, we get the equation for molar mass
M = ![]() ------
(3)
------
(3)
Dalton’s Law of Partial Pressures:
This law states that “the total pressure exerted by a mixture of
non-reactive gases is equal to the sum of the partial pressures of individual
gases” i.e., the pressures which these gases would exert if they were enclosed
separately in the same volume and under the same conditions of temperature.
pTotal = p1 + p2 + p3 +......(at constant T, V)
where,
pTotal the total pressure exerted by the mixture of gases,
p1
+ p2 + p3 +...... is the sum of the partial pressures of
individual gases.
Gases are generally collected over water and therefore contain some water vapour. The pressure of dry mixture of gases can be calculated by subtracting vapour pressure of water from the pressure of the resulting mixture of gases. Pressure exerted by saturated water vapour is called aqueous tension.
pDry gas = pTotal + Aqueous tension
Let us assume three gases enclosed in volume V at temperature T exert partial pressures p1, p2, and p3, then,
p1 = ![]() as only number of moles of gas n will change
as only number of moles of gas n will change
p2 = ![]()
p3 = ![]()
pTotal = p1 + p2 + p3
therefore,
pTotal = n1 ![]() + n2
+ n2
![]() + n3
+ n3
![]()
= n1 + n2 + n3 ![]()
![]() =
=
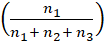
![]()
= ![]()
Let ![]() 1 =
1 = ![]() be the mole fraction of first
gas. Then,
be the mole fraction of first
gas. Then,
p1 = ![]() 1 × pTotal
1 × pTotal
Similarly, p2 = ![]() 2 × pTotal
2 × pTotal
p3 = ![]() 3 × pTotal
3 × pTotal
Assuming there are i number of gases, then we get a general equation,
pi = ![]() i × pTotal
i × pTotal
Problems:
1. A neon-dioxygen mixture contains 70.6 g dioxygen and 167.5 g neon. If
the pressure of the mixture of gases in the cylinder is 25 bars. What is the
partial pressure of dioxygen and neon in the mixture?
Solution:
We have,
m1 = 70.6 g
m2 = 167.5 g
pTotal = 25 bars
p1 = ?
p2 = ?
M = Relative atomic mass × Molar mass
constant (1 g/mol)
M1 = 32 ×1
= 32 g/mol
M2 = 20.18 ×1
= 20.18 g/mol
n = ![]()
n1 = ![]()
= 2.21 g/mol
n2 = ![]()
= 8.30 g/mol
Mole fraction of dioxygen,
![]() 1 =
1 = ![]()
= 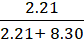
= 0.21
Mole fraction of neon,
![]() 2 =
2 = ![]()
= 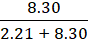
= 0.79
Partial pressure of dioxygen,
p1 = ![]() 1 × pTotal
1 × pTotal
= 0.21 × 25
= 5.25 bars
Partial pressure of neon,
p2 = ![]() 2 × pTotal
2 × pTotal
= 0.79 × 25
= 19.75 bars