Applications of Chemical Equilibrium

Some of the important applications of equilibrium constants are as follows :

·        Prediction of completion of reaction

·       Prediction about the forward or reverse direction of the reaction

·       Calculation of equilibrium constant

Ø Prediction of completion of reaction:

The value of equilibrium constant shows proportion of completion of the reaction. If the value of Kc > 1, then more proportion of products will be obtained, i.e. the reaction of getting products from the reactants will be towards completion.  If the value of KC is less than 1, then the proportions of reactants will be more as compared to products and so there will be decrease in the tendency for the completion of the reaction. If value of KC is 1, then the proportions of reactants and products will be in equilibrium state.

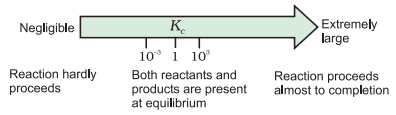
Dependence of extent of reaction on Kc

Ø Prediction about the forward or reverse direction of the reaction:

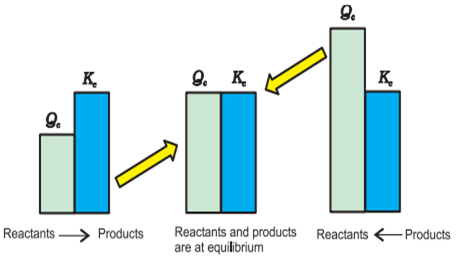
The predictin about the reaction at any stage will occur in which direction can be decided from the value of equilibrium constant. For this we have to calculate the reaction quotient (QC). As the value of Kc for the reaction Aa + Bb ⇋ cC + Dd

Kc  =    = Qc

If Qc < Kc’ or Kc > Qc’ then the reaction will occur in forward direction, i.e. from reactants to products. If Qc = Kc’ then the reaction will occur in reverse reaction, i.e. from products to reactants. If Qc = Kc’ , the reaction will remain in equilibrium.

 

Ø Calculation of equilibrium constant:

If we know the concentrations of reactants and products at equilibrium time we can calculate the value of equilibrium constant and if the initial concentration of the reactants and the value of equilibrium constant are known, equilibrium concentrations can be calculated. For this the following steps are to be followed.

Step1: Write chemical reaction in balanced form.

Step 2: (a) Mention the initial concentrations of reactants and products below them and (b) Mention the changes that take place when equilibrium is reached. Mention concentration in mollit -1 or pressure in bar. Write  for the unknown concentrations and then mention their stoichiometry.

Step 3: Put the values of equilibrium concentration in the equation of chemical equilibrium and solve the equation. If quadratic equation is obtained, find out the two values using formula for it and determine the acceptable value.

Step 4: From the value of, determine the acceptable value.

Step 5: Verify the value of equilibrium constant by putting the values of equilibrium concentrations in the equation for equilibrium constant.

Ø Relationship between equilibrium constant K, Reaction quotient Q and Gibbs energy G:

The value of Kc for a reaction does not depend on the rate of the reaction. However, as you have studied in Unit 6, it is directly related to the thermodynamics of the reaction and in particular, to the change in Gibbs energy, ∆G. If

·        ∆G is negative, then the reaction is spontaneous and proceeds in the forward direction.

·        ∆G is positive, then reaction is considered non-spontaneous. Instead, as reverse reaction would have a negative ∆G, the products of the forward reaction shall be converted to the reactants.

·        ∆G is 0, reaction has achieved equilibrium; at this point, there is no longer any free energy left to drive the reaction. A mathematical expression of this thermodynamic view of equilibrium can be described by the following equation:

∆G = ∆G0 + RT lnQ

Where, G0 is standard Gibbs energy.

At equilibrium, when ∆G = 0 and Q = Kc’ the equation becomes,

∆G = ∆G0 + RT ln K = 0

∆G0 = – RT lnK

 lnK = – ∆G0 / RT

Taking antilog of both sides, we get,

K =

Hence, using the equation, the reaction spontaneity can be interpreted in terms of the value of ∆G0.

·         If ∆G0 < 0, then –∆G0 /RT is positive, and K =  >1, making K >1, which implies a spontaneous reaction or the reaction which proceeds in the forward direction to such an extent that the products are present predominantly.

·         If ∆G0 > 0, then –∆G0 /RT is negative, and K = < 1, that is , K < 1, which implies a non-spontaneous reaction or a reaction  which proceeds in the forward direction to such a small degree that only a very minute quantity of product is formed.