Periodic Motion

A motion which repeats itself in definite interval of time is called Periodic Motion.

Examples:

1. motion of sun around earth

2. motion of arms of a clock

3. motion of simple pendulum

4. The Halley’s comet appears after every 76 years

Period as a Function of Time

ü Time need for an object to complete one oscillation^* is called time period.

(or)

ü The time after which the body retraces its path is called time period.

ü It is denoted by ‘ T ’

(Note: Oscillation -when an object moves to and fro on either side of a point in definite time interval, then this motion is said to be oscillatory motion or vibratory motion)

Example

1 .if a pendulum makes 24 complete back and forth cycles of oscillation in 12 seconds then its period is ?

Solution:

Given data

There are 12 seconds for 24 oscillations thus time period is

T=12 seconds/24 cycles= 0.50 seconds

2. Motion of a mass suspended from a spring

3. Motion of simple pendulum

Frequency as a Function of Time

ü The number of oscillation or vibration produced by the particle in one second is known as Frequency.

ü It is denoted by ‘γ’

(Frequency)

Example

1. If a pendulum makes 24 complete back and forth cycles of oscillation in 12 seconds then its period is 0.50 seconds. Find the frequency ?

Solution:

Given Data

Time Period = 0.50 seconds

Frequency (γ) = 1/T

= 1/0.50 seconds

= 2 Hz

Displacement as a Function of Time

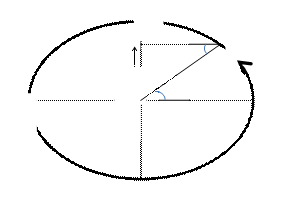
ü The distance travelled by the oscillating particle or an object at any instance of time ‘t’ from its mean position is known as displacement (y).

ü When the particle reaches A from X after time period t , the displacement of the particle along Y axis y (i.e., shown in the figure).

Let us consider the ∆OAB,

Since OA= y, OB= and =ωt

Here the displacement is a function of time i.e., g(t)

Hence

If the argument of the function (ωt) is incremented by an integral multiple of 2π radians, the value of the function remains the same.

The function f (t) is then periodic and its period T is given by,

Then the function f (t) is periodic with period T

It is same for cosine function also.

………..(1)

Let’s take

By using trigonometric identities, the linear combination of sine and cosine functions are,(i.e., equ (1)) becomes,

Here D and ϕ are constants,

D= and ϕ=

Hence we can conclude that Any periodic function can be expressed as a superposition of sine and cosine functions of different time periods with suitable coefficients.

ü The vector quantity which varies uniformly with time in an oscillatory motion is called displacement.

ü the vibrating particle‘s amplitude is defined as its maximum displacement from the mean position.