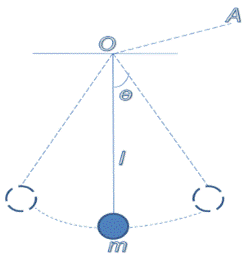
Simple pendulum

· A simple pendulum consists of a heavy particle suspended from a fixed support through a light inextensible string.

· A simple pendulum in which a particle of mass m is suspended from the fixed support O through a light string of length L

· The system can stay in equilibrium if the string is vertical. This is the mean or equilibrium position.

· If the particle is pulled aside and released, it oscillates in a circular arc with the centre at the point of suspension O.

· The position of the particle at any time can be described by the angle ɵ between the string and the vertical.

· The mean position or the equilibrium position corresponds to ɵ = O.

· The particle makes pure rotation about the horizontal line OA, which is perpendicular to the plane of motion.

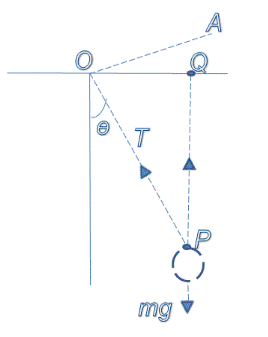
Let OQ be the horizontal line in the plane of motion.

Let PQ be the perpendicular to OQ.

Forces acting on the particle are,

1. The weight mg

2. The tension T

The magnitude of the torque of mg about OA is

The torque tries to bring the particle back towards ɵ = 0. Thus, we can write

We see that the resultant torque is not proportional to the angular displacement and hence the motion is not angular simple harmonic.

However, if the angular displacement is small, sine is approximately equal to 0 (expressed in radians) and the above equation may be written as

(1)

Thus, if the amplitude of oscillation is small, the motion of the particle is approximately angular simple harmonic.

The moment of inertia of the particle about the axis of rotation OA is

(2)

The angular acceleration is

(3)

Substitute equations (1) & (2) in (3)

note :

(4)

This is the equation (4) of an angular simple harmonic motion.

The constant represents the angular frequency.

The time period T is
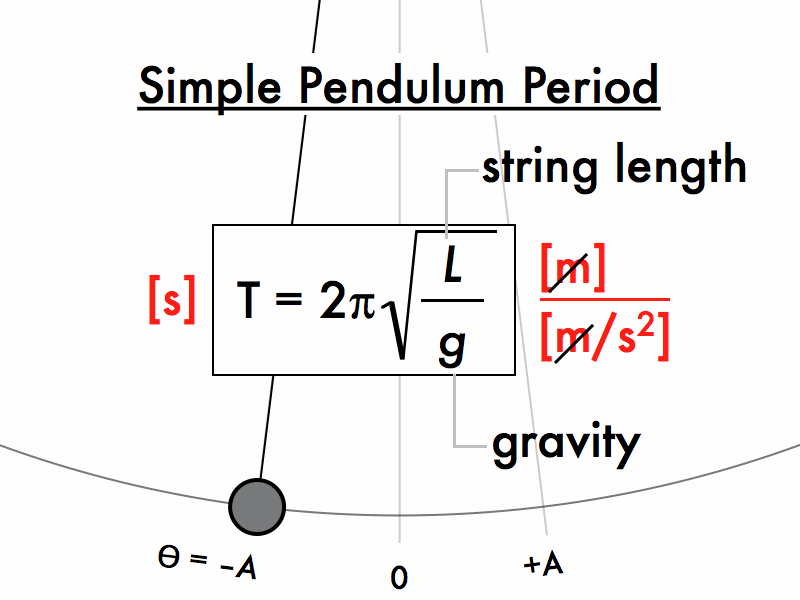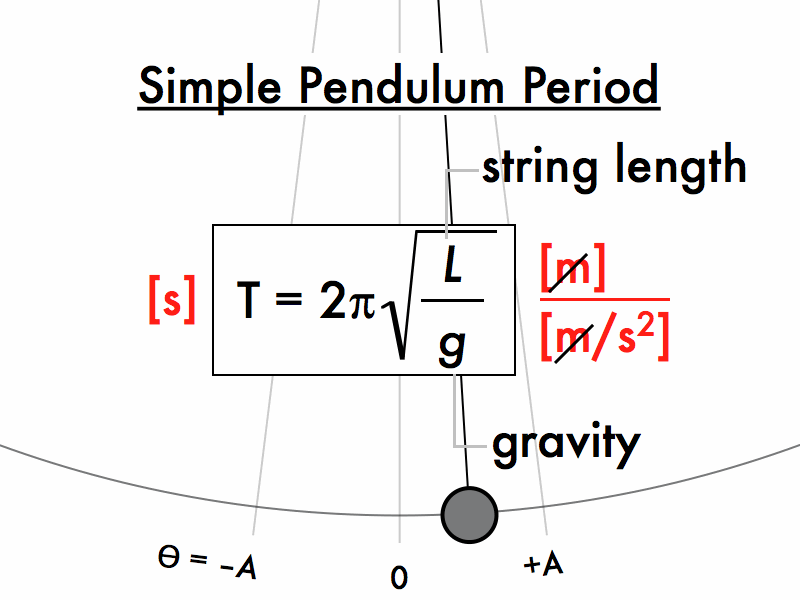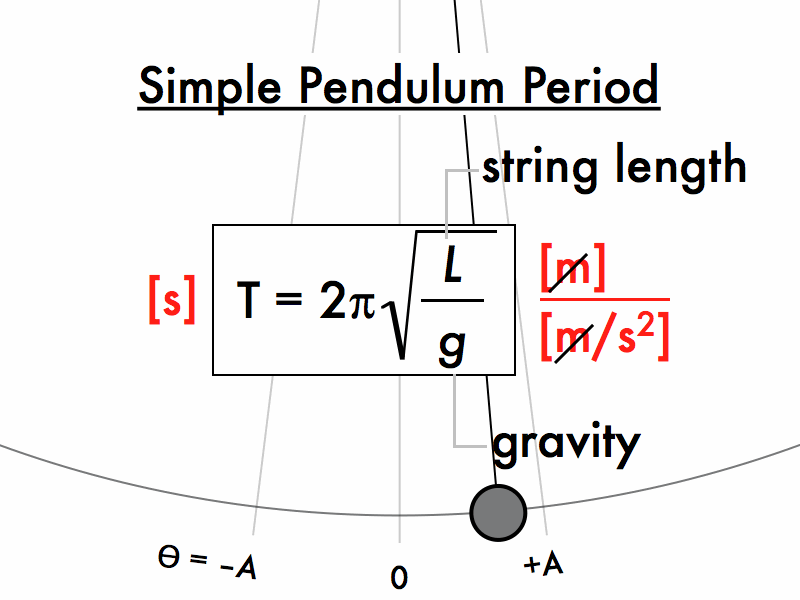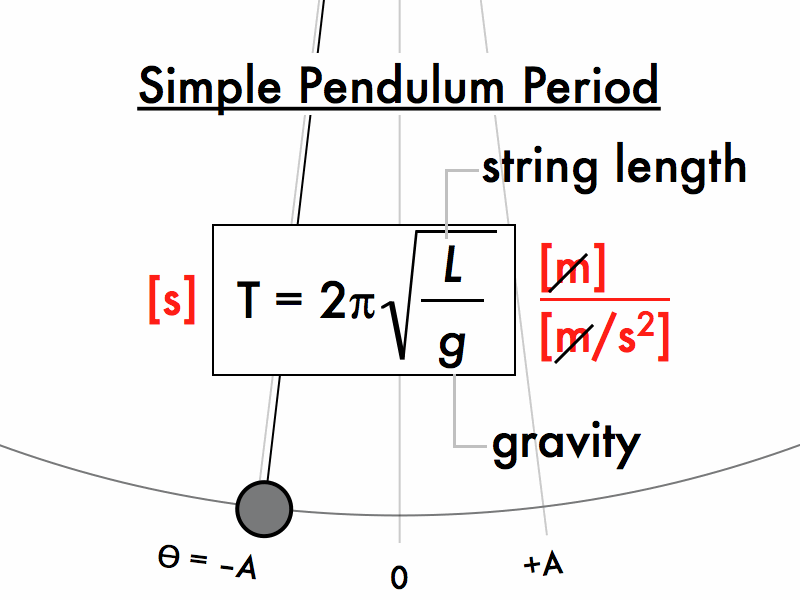
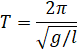