Scalar and Vector Quantities
In physics, quantities are
classified as -
·
Scalar quantities
·
Vector quantities
Basically, the difference between
the scalar and vector quantities is that a direction is associated with a
vector but not with a scalar.
Scalar
Quantities:
The quantities for which, complete
information is obtained by knowing their values only are called scalars, e.g.
temperature, time, mass, density, volume, work etc. A scalar is represented by
a number showing its magnitude in a proper unit.
The combination or associations of
scalar quantities follow the laws of ordinary algebra. Addition, subtraction,
multiplication and division can be done like those of usual numbers.
Vector
Quantities:
The quantities, which need the
direction as well as their values (magnitudes), to be completely known, are
called vectors, e.g. velocity, acceleration, force, torque, area, displacement
etc.
A vector quantity is represented
by putting an arrow on the symbol of that quantity or as a bold letter. For
example, the force vector is shown as 
or F the velocity vector is
represented as 
or v. The
value of the vector quantity is shown by putting the symbol of that quantity in
modulus (i.e. between two vertical bars) or by writing that symbol without the arrow.
E.g., The value of 
is shown by || or A. The vector quantities obey
specific laws of combination.
Position and Displacement Vectors:
To represent the position of a
body we have to mention the reference point which is usually taken as the
origin of coordinate axes. Suppose a body moves along the path PQRS as shown in
the below figure. At time t1 it is at point Q.
The vector 
formed by joining the origin
O with the point Q is called the position vector of the body at time t1.
Suppose at time t2, the body reaches the point R. Then, the
Vector 
formed by joining the origin
O with the point R is called the position vector of the body at time t2.
During time t2 − t1 it
reaches from Q to R. Hence its displacement vector is shown by
.
Here a noteworthy point is that the
value of the displacement vector is the minimum distance between the initial
position and the final position.
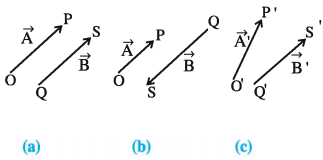
Equality of Vectors:
Equal Vectors: If the values and the directions
of two vectors are equal, then they are called equal vectors. (below figure a)
Parallel Vectors: The vectors with the same
direction are called parallel vectors. (The magnitudes of such vectors can be
equal or different). (below figure a)
Antiparallel Vectors: The vectors having mutually opposite
directions are called antiparallel vectors. (below
figure b)
Aparallel Vectors: The vectors which are not parallel
or antiparallel to each other are called aparallel
vectors. (below figure c)
|
|
|
|
