Kepler's Laws of Planetary Motion

To explain the motion of the planets, Kepler formulated the following three laws:

1. Law of Orbits (First law):

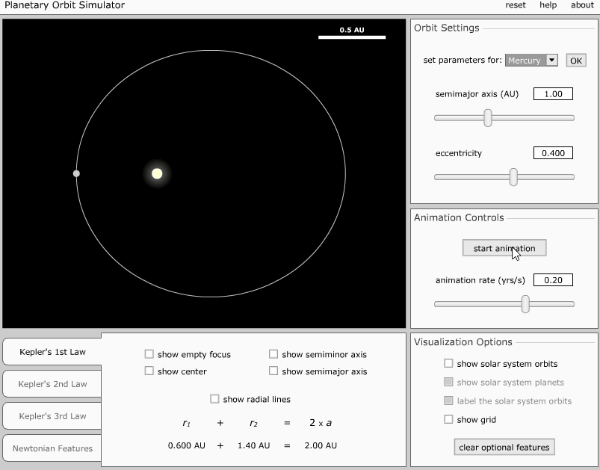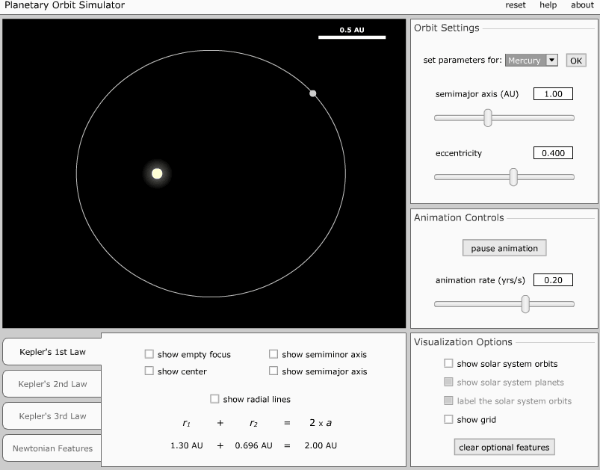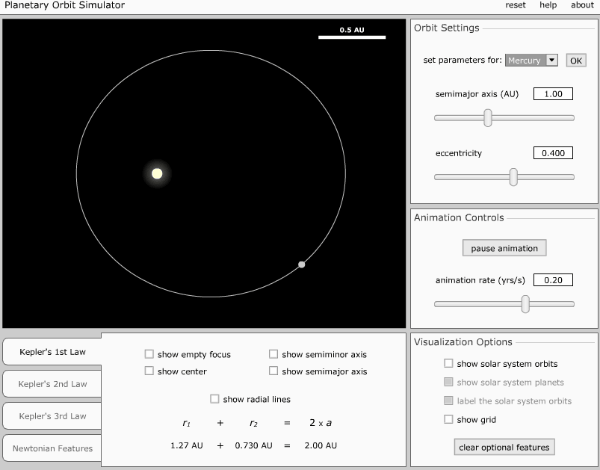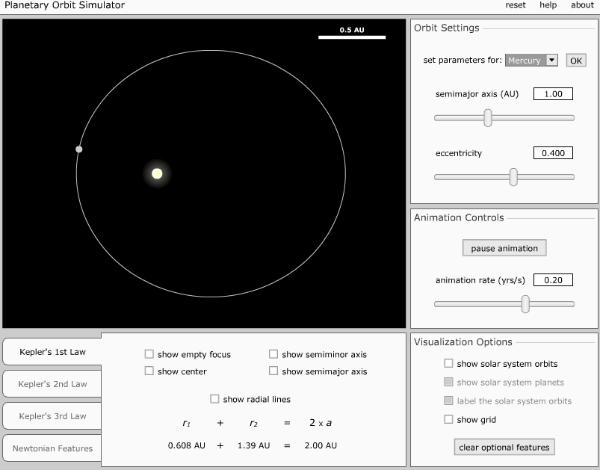
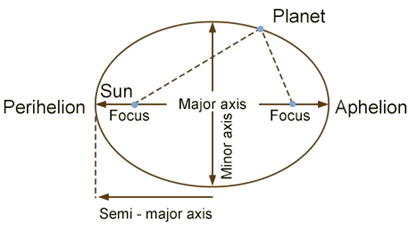
Each planet revolves around the sun in an elliptical orbit with the sun situated at one of the two foci.

As shown in figure, the planets move around the sun in an elliptical orbit. An ellipse has two foci S and S’ the sun remains at one focus S.

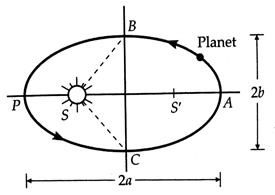
Elliptical orbit of a planet, PA = 2a = major axis, BC = 2b = minor axis.

The points P and A on the orbit are called the perihelion and the aphelion and represent the closest and farthest distances from the sun respectively. The orbits of Pluto and Mercury are highly elliptical. The orbits of Neptune and Venus are circular. The orbits of other planets have slight ellipticity and may be taken as nearly circular.

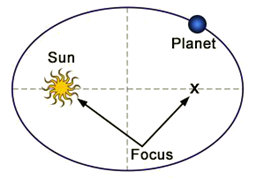
Kepler's first law

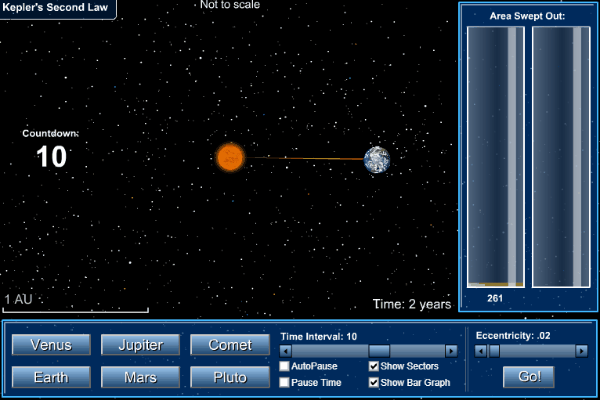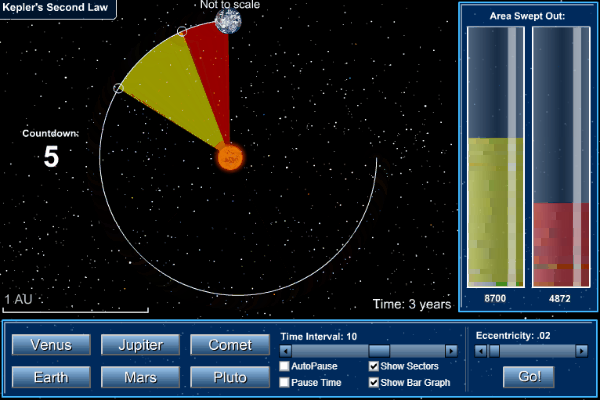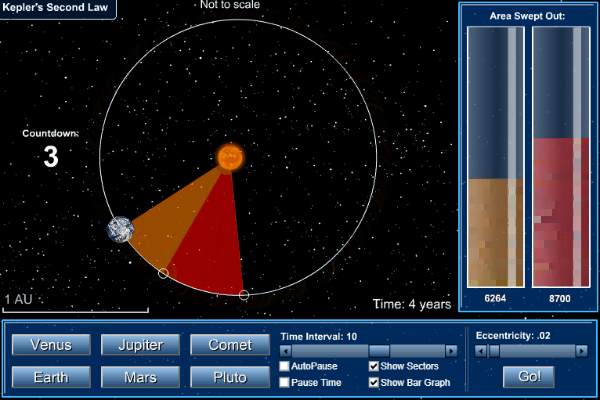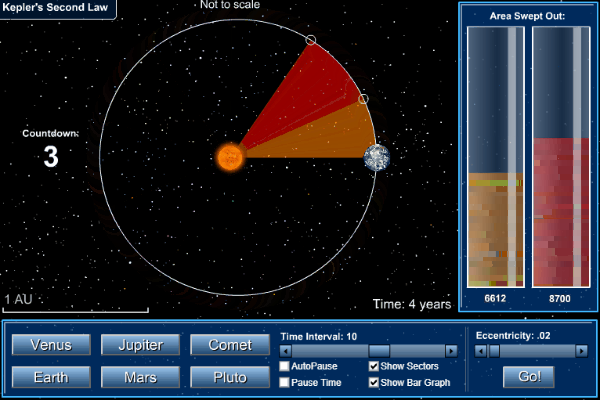
2. Law of Areas (Second law):

The radius vector drawn from the sun to a planet sweeps out equal areas in equal intervals of time i.e., the areal velocity (area covered per unit time) of a planet around the sun is constant.


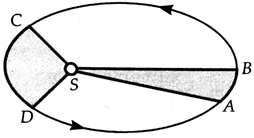
Kepler's second law of areas

Suppose a planet takes same time to go from position A to B as in going from C to D. Kepler’s second law, the areas ASB and CSD second law, (covered equal time) must be equal. Clearly, the planet covers a larger distance CD when it is near the sun than AB when it is farther away in the same interval of time. Hence the linear velocity of a planet is more when it is closer to the sun than its linear velocity when away from the sun.

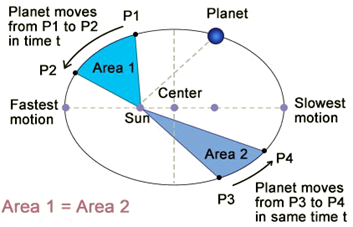
Kepler's second law

3. Law of Periods (Third law):

The square of the period of revolution of a planet around the sun is proportional to the cube of the semimajor axis of its elliptical orbit.

If T is the period of revolution of a planet and R is the length of semimajor axis of its elliptical orbit, then

T2 α R3

T2 = KR3

where K is a proportionality constant.

For two different planets, we can write

 =

Thus larger the distance of a planet from the sun, the larger will be its period of revolution around the sun. The period of revolution of the farthest planet Pluto around the sun is 247 years while that of the nearest planet mercury is 81 days.

Kepler's third law

Problems:

1. The distance of Venus from the sun is 0.72 AU. Find the orbital period of Venus.

Solution:

            For earth,

                    = 1 year,  = 1 AU

            For the planet Venus,

                    = ,  = 0.72 AU

                   =

            = (1)2 ×

            = 0.37 yr2

                    =

= 0.61 yr

= 223 days

 

2. If the earth be one half its present distance from the sun, how many days will the present distance from the sun, how many will the present one year on the surface of earth change?

Solution:

            Here

       = 365 days,  = r,  =

                   =

                        = 365

                        = 129 days

Decrease in the number of days in one year

            = 365 – 129

            = 236 days

 

3. The distance of planet Jupiter from the sun is 5.2 times that of earth. Find the period of revolution of Jupiter around the sun.

Solution:

                     =     

            = 1 ×

            = 11.86 years

 

4. The planet Neptune travels around the sun with a period of 165 years. Show that the radius of its orbit is approximately 30 times that of earth orbit, both being considered as circular.

Solution:

            Here,

                    = 1 year

                    = 165 years

                   =

                        =

= 30

 

5. A geostationary satellite is orbiting the earth at a height 6R above the surface of earth where R is the radius of earth. Find the time period of another satellite at a height of 2.5R from the surface of earth in hours.

Solution:

            Here = 6R + R

                                    = 7R,

                   = 24 h

                    = 2.5 R + R

            = 3.5 R

                   = ?

                                =

                        =

                        =

                        = 6 h

                       

6. The radius of earth’s orbit is 1.5 × 108 km and that of Mars is 2.5 × 1011 m. In how many years, does the mars complete in one revolution?

Solution:

            Here  = 1.5 × 108 km

                           = 1.5 × 1011 m

                       = 2.5 × 1011 m

                      =                       

                          =

                          =

                          = 2.15 years

 

7. A planet of mass m around the sun of mass M in an elliptical orbit. The maximum and minimum distance of the planet from the sun are and  respectively. Find the relation for the time period of the planet in terms of  and .

Solution:

            Semimajor axis of the elliptical orbit of the plane around the sun,

                          r =

            According to kepler’s third law

                            or    

                         

 

8. Calculate the period of revolution of Neptune around the sun, given that diameter of its orbit is 30 times the diameter of earth’s orbit around the sun, both orbit around the sun, both orbits being assumed to be circular.

Solution:

            According to Kepler’s law of periods,                            =

But            = 30 and TE = 1 year

                   =

            = (1)2 × (30)3

            = 27000

                              TN =

            = 164.3 years

 

9. In kepler’s law of periods: T2 = kr3, the constant k = 10−13 s2 m−3. Express the constant k in days and kilometres. The moon is at distance of 3.84 × 105 km from the earth. Obtain its time period of revolution in days.

Solution:

            Given                     k =

            As                          1s = day    and   1 m =   km−3

            ∴                             k = 10−13 ×   kms−3

            = 1.33 × 10-14 d2 km−3

            For the moon,     r = 3.84 × 105 km

                  T2 = kr3

= 1.33 × 10-14 × (3.84 × 105)3

            = 27.3 days

 

10. In a imaginary planetary system, the central star has the same mass as our sun, but is brighter so that only a planet twice the distance between the earth and sun can support life. Assuming biological evolution (including aging process etc.) on that planet similar to ours, what would be the average life span of a ‘human’ on that planet in terms of its natural year? The average life span of a human on the earth may be taken to be 70 years.

Solution:

            According to Kepler’s law of periods,

       =

            Here,

T1 = average life span of a human on the earth = 70 years

T2 = average life span of a human on the planet = ?

R1 = Distance between the earth and planet = 2R2

R2 = Distance between the earth and sun

            ∴    =

                  = 8

                         =

            ∴           =

                              = 25 planet years

 

11. The planet Mars has two moons, Phobos and Delmos. (i) Phobos has a period 7 hours, 39 minutes and an orbital radius of  . Calculate the mass of Mars.

(ii) Assume that earth and mars move in circular orbits around the sun,with the martian orbit being 1.52 times the orbital radius of earth. What is the length of martian year in days?

Solution:

(i) Here      =

                                 =

                        = 459 min

= 459 × 60 s

            Mass of Mars,

                             =

                        =

                        = 6.48 × 1023 kg

            (ii) Here   =                  

                               =

                        According to Keplers law of periods,

                               =

                        ∴    =

                        =  × 365

                        = 684 days

 

12. The distance of two planet from the sun are 1013 m and 1012 m respectively. Find the ratio of time periods and speeds of the two planets.

Solution:

            Here  = 1013 m,  = 1012 m

            For kepler’s third law,

        =

=

= 10

If  and  are orbital speed of the planets, then

       =      and      =

        =  

=

=

=

= 1