Newton's Universal Law of Gravitation
Discovery of Newton's
Law of Gravitation:
One day in the year 1665, seeing an
apple falling from a tree, Newton was inspired to think about the law of
gravitation. He thought that the force which attracts the apple towards the
earth might be the same as the force attracting the moon towards the earth. By
comparing the acceleration due to gravity on the earth with the acceleration
required to keep the moon in orbit around the earth, Newton was able to deduce
the law of gravitation as discussed below
Newton assumed that the moon revolved
around the earth in a circular orbit of radius R (= 
m), as shown in below figure.
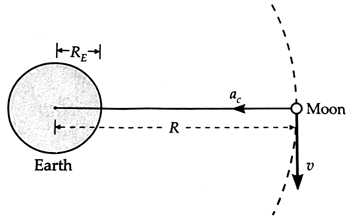
Centripetal
acceleration of the moon
Period of moon around the earth,
T = 27.3
days
= 
Speed
of the moon,
= 
= 
= 
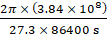
Centripetal
acceleration of the moon,
= 
= 
= 
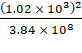
------ (i)
Acceleration
due to gravity at the earth's surface,
g = 
Clearly 
. Newton assumed that both acceleration
of the moon and acceleration of the falling object are provided by earth's
gravitational attraction. Newton argued that force and hence the acceleration
produced must decrease with distance from the centre
of the earth. From the relative values of and 
, he proposed that the gravitational
force should be inversely proportional to the square of the distance. If 
is the radius of the earth, then
= 
= 
Newton
knew that 
= 
∴
= 
= 
=
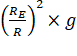
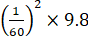
This value is in close argument with the value obtained in
equation (i), thus verifying the inverse square law.
It is called Newton's moon test.
Newton further analysed
that the gravitation exerted by an object should be proportional to its mass.
By the third law of motions the second object should exert an equal and opposite
force on the first one. This force should be proportional to the mass of the
second object. Taking into account all these facts, he arrived at his famous
universal law of gravitation.
Statement of Newton's Law of
Gravitation:
In 1687, Newton published the universal law of gravitation in his
book Principia. This law can be stated as follows:
Every particle in the universe attracts every other particle with a force which is directly proportional to the
product of their masses and inversely proportional to the square of the
distance between them. This force acts along the line joining the two
particles.
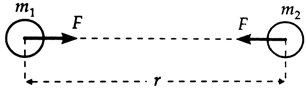
Law of gravitation
Consider two bodies of masses 
and 
and separated by distance 
. According to the law of gravitation,
the force of attraction 
between them is such that
and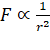 
∴
F = 
Where G is a constant called
universal gravitational constant.
Definition of G:
If = = 1 and = 1, then
F = G
The universal gravitational constant may be defined as the force of attraction between two
bodies of unit mass each and placed unit distance apart.
In SI, the gravitational constant is equal to the force
attraction between two
bodies of 
kg each and placed m apart.
In cgs system, the gravitational constant is
equal to the force of attraction between two bodies of 1 g each and placed 1 cm
apart.
Dimensions of G:
As F
=
G = 
Dimensions of G =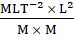 
= 
Units of G:
As G
=
S.I. Unit of G = 
= 
Similarly, cgs unit of G = 
Value of G:
In SI,
G
= 
In cgs system, G
= 
The value of G does not
depend on the nature and size of the bodies. It also does not depend on the
nature of the medium between the two bodies. That is why G is called universal gravitational constant.
Cavendish's Experiment for the Determination of G:
The value of the gravitational constant G was first determined experimentally by English scientist Henry
Cavendish in 1798. The apparatus used is shown in below figure.
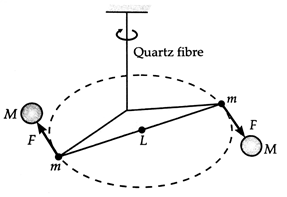
Cavendish method
Here two small identical spheres of lead, each of mass m are connected to the two ends of a
light rod to form a dumb-bell. The rod is supported by a vertical length of
quartz fibre. Two large lead spheres of mass M each are placed near the ends of the
dumb-bell on the opposite sides in such a way that all the four spheres lie on
a horizontal circle. The small spheres move towards the larger ones under the
gravitational attraction,
F = 
where 
is the distance between the
centre of the large and its neighbouring small sphere.
The forces on the two small spheres form a couple which exerts a
torque. This torque deflects the rod and twists the suspension till such time
as the restoring torque of the fibre equals the
deflecting gravitational torque. The angle of deflection 
is noted by measuring the
deflection of a light beam by a lamp and scale arrangement. Let 
be the length of the light
rod.
Then,
Deflecting torque = F × L
= 
Restoring torque = 
where 
is the restoring torque per
unit angle of twist and is called torsion constant of the suspension fibre.
In rotational equilibrium, both the torques are equal and
opposite.
=
G = 
Knowing all the quantities on the right hand side from the experiment,
the value of G can be determined.
Since Cavendish's experiment, the measurement of G has been improved upon. The currently
accepted value is
G = 
|
|
|
|
