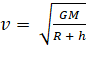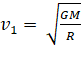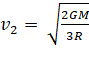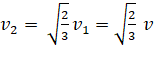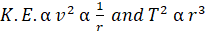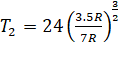Problems
1. If 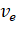 and
and 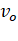 represent the escape velocity and
orbital velocity of a satellite corresponding to a circular orbit of radius R, then
represent the escape velocity and
orbital velocity of a satellite corresponding to a circular orbit of radius R, then
A) ![]()
B) ![]()
C) ![]()
D)
![]() and
and
![]() are not related
are not related
Solution: B
![]() =
= ![]() and
and ![]() =
= ![]()
![]()
2. An earth satellite of mass m revolves in a circular orbit at a height h from the surface of the earth. R is the radius of the earth and g is acceleration due to gravity at the surface of the earth. The
velocity of the satellite in the orbit is given by
A) ![]()
B) ![]()
C) ![]()
D) 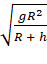
Solution: D
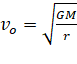
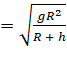
3. A satellite which is geostationary in a particular orbit is
taken to another orbit. Its distance from the centre of
earth in new orbit is 2 times that of the earlier orbit. The time period in the
second orbit is
A) ![]()
B)![]()
C) ![]()
D)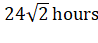
Solution: B
![]()
If r becomes double then time
period will becomes (2)3/2 times. So new time period will be ![]() hr
i.e.
hr
i.e. ![]() .
.
4. Two satellites A
and B go round a planet P in circular orbits having radii 4R and R respectively. If the speed of the satellite A is 3V, the speed of the
satellite B will be
A) ![]()
B)![]()
C) ![]()
D)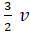
Solution: B
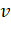 =
=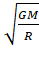 and
and 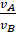 =
= 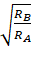 =
= 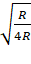 =
= 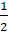
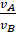 =
= 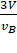
= 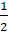
∴ 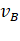 = 6V
= 6V
5. The orbital velocity of an artificial satellite in a
circular orbit just above the earth's surface is v. For a satellite orbiting at an altitude of half of the earth's
radius, the orbital velocity is
A) ![]()
B)![]()
C) ![]()
D)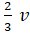
Solution: C
For first satellite 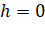 ,
,
For second satellite 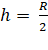 ,
,
6. In a satellite if the time of
revolution is T, then K.E. is
proportional to
A) ![]()
B) ![]()
C) ![]()
D) 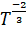
Solution: D
V = 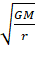
7. A satellite is moving around
the earth with speed v in a circular
orbit of radius r. If the orbit
radius is decreased by 1%, its speed will
A) Increase by 1%
B) Increase
by 0.5%
C) Decrease
by 1%
D) Decrease by 0.5%
Solution: B
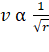 % increase in speed =
% increase in speed = 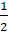 (%
decrease in radius)
(%
decrease in radius)
= ![]() (1 i.e., speed will increase by 0.5%)
(1 i.e., speed will increase by 0.5%)
8. Orbital velocity of earth's
satellite near the surface is 7 km/s. When the radius of the orbit is 4 times
than that of earth's radius, then orbital velocity in that orbit is
A) 3.5 km/s
B) 7
km/s
C) 72
km/s
D) 14 km/s
Solution: A
![]()
If orbital radius becomes 4 times then
orbital velocity will become half. i.e., ![]() = 3.5 km/s
= 3.5 km/s
9. The mean radius of the earth is 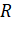 , its angular speed on its own
axis is
, its angular speed on its own
axis is 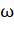 and the acceleration due to gravity at earth's
surface is
and the acceleration due to gravity at earth's
surface is 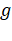 . The cube of the radius of the
orbit of a geostationary satellite will be
. The cube of the radius of the
orbit of a geostationary satellite will be
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: D
Orbital velocity ![]() =
= ![]() and
and ![]() .
.
This gives ![]() .
.
10. Periodic time
of a satellite revolving above Earth’s surface at a height equal to 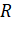 , radius
of Earth is [
, radius
of Earth is [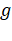 is acceleration due to gravity at Earth’s
surface
is acceleration due to gravity at Earth’s
surface
A) 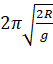
B) ![]()
C) ![]()
D) ![]()
Solution: B
T = ![]()
= ![]()
= ![]()
11. Given radius of Earth ‘R’ and
length of a day ‘T’ the height of a
geostationary satellite is [G-Gravitational
Constant, M-Mass of Earth]
A) 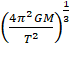
B) ![]()
C) ![]()
D) ![]()
Solution: C
![]()
![]()
![]() =
= ![]()
![]() =
= ![]()
12. A geo-stationary satellite is orbiting the earth at a height of 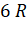 above the surface of earth,
above the surface of earth, 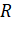 being the radius of earth. The time period of another
satellite at a height of
being the radius of earth. The time period of another
satellite at a height of 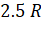 from the surface of earth is
from the surface of earth is
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: D
Distances of the satellite from the centre are 7 R and 3.5 R respectively.
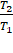 =
= 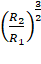
= 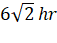
13. The gravitational force
between two stones of mass 1 kg each separated by a distance of 1 metre in
vacuum is
A) Zero
B) 6.675
× 10−5 newton
C) 6.675×10−11 newton
D) 6.675×10−8 newton
Solution: C
F = ![]()
= ![]()
= ![]()
14. Two
particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. The
speed of each particle is
A) ![]()
B) ![]()
C) ![]()
D)![]()
Solution: C
Centripetal force provided by the
gravitational force of attraction between two particles i.e.
![]() =
= ![]()
![]()
15. The earth (mass = ![]() )
revolves round the sun with angular velocity
)
revolves round the sun with angular velocity ![]() in
a circular orbit of radius
in
a circular orbit of radius ![]() .
The force exerted by the sun on the earth in newtons,
is
.
The force exerted by the sun on the earth in newtons,
is
A)![]()
B) Zero
C) ![]()
D)![]()
Solution: D
![]() ,
, ![]() ,
, ![]()
The force exerted by the sun on the earth ![]()
By substituting the value we can get, ![]()
16. The
distance of the centres of moon and earth is D. The mass of earth is 81 times the mass of the moon. At what
distance from the centre of the earth, the gravitational force will be zero?
A)![]()
B) ![]()
C) ![]()
D)![]()
Solution: D
Force will be zero at the point of zero intensity
![]()
![]()
= ![]()
17. The
mass of the moon is 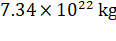 and the radius is
and the radius is 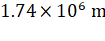 . The value
of gravitation force will be
. The value
of gravitation force will be
A)![]() 1.45 N/kg
1.45 N/kg
B) 1.55 N/kg
C) ![]()
D)![]()
Solution: D
g
= ![]()
= ![]()
= ![]()
18. Mass
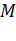 is divided into two parts
is divided into two parts 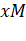 and
and 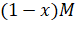 . For a given
separation, the value of
. For a given
separation, the value of 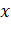 for which the gravitational attraction between
the two pieces becomes maximum is
for which the gravitational attraction between
the two pieces becomes maximum is
A)![]()
B) ![]()
C) ![]()
D)![]()
Solution: A
![]()
= ![]()
For
maximum Force
![]() = 0
= 0
![]() =
= ![]()
= 0
![]() =
= ![]()
19. Two
identical solid copper spheres of radius R
placed in contact with each other. The gravitational attraction between them is
proportional to
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: C
F
= ![]()
=
![]()
=
![]()
![]()
20. The
distance of Neptune and Saturn from sun are nearly 1013 and 1012
meters respectively. Assuming that they move in circular orbits, their periodic
times will be in the ratio
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: C
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
21. The period of a satellite in a
circular orbit of radius 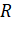 is
is 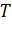 , the
period of another satellite in a circular orbit of radius
, the
period of another satellite in a circular orbit of radius 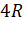 is
is
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: C
![]()
= ![]()
![]()
22. A planet moves around the sun. At a given point 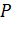 , it is
closest from the sun at a distance
, it is
closest from the sun at a distance 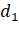 and
has a speed
and
has a speed 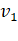 . At
another point
. At
another point 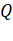 , when
it is farthest from the sun at a distance
, when
it is farthest from the sun at a distance 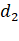 , its speed
will be
, its speed
will be
A) ![]()
B) ![]()
C) ![]()
D)![]()
Solution: C
Angular
momentum remains constant
![]()
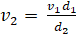
23. The rotation period of an earth satellite close to the
surface of the earth is 83 minutes. The time period of another earth satellite
in an orbit at a distance of three earth radii from its surface will be
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: C
For first satellite 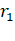 = R and
= R and 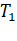 =
= 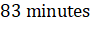
For second satellite 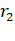 = 4R
= 4R
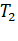 =
= 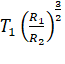
= 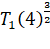
= 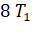
= 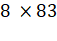
= 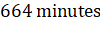
24. A planet
revolves around sun whose mean distance is 1.588 times the mean distance between
earth and sun. The revolution time of planet will be
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: D
![]() =
= ![]()
= ![]()
= 2
![]() =
2 years
=
2 years
25. A satellite 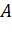 of mass
of mass 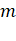 is at a distance of
is at a distance of 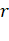 from the centre of the earth. Another
satellite
from the centre of the earth. Another
satellite 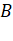 of mass
of mass 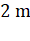 is at a distance of
is at a distance of 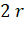 from the earth's centre. Their time periods
are in the ratio of
from the earth's centre. Their time periods
are in the ratio of
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: D
Mass of the satellite does not effects on
time period
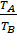 =
= 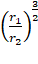
=
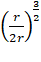
= 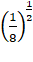
= 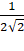
26. The
period of revolution of planet 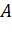 around the sun is 8 times that of
around the sun is 8 times that of 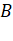 . The
distance of
. The
distance of 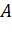 from the sun is how many times greater than that
of
from the sun is how many times greater than that
of 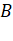 from the sun
from the sun
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: C
![]()
![]()
![]()
![]()
27. If
the radius of earth's orbit is made 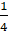 , the
duration of an year will become
, the
duration of an year will become
A) 8
times
B) ![]()
C) ![]()
D) ![]()
Solution: C
![]()
If r made half then T will become ![]() .
.
28. The
earth revolves round the sun in one year. If the distance between them becomes
double, the new period of revolution will be
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: B
![]()
= ![]()
= ![]()
![]()
29. The
maximum and minimum distances of a comet from the sun are 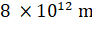 and
and 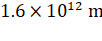 . If its
velocity when nearest to the sun is
. If its
velocity when nearest to the sun is 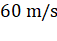 , what
will be its velocity in m/s when it is farthest
, what
will be its velocity in m/s when it is farthest
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: A
By conservation of angular momentum ![]() = constant
= constant
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
30. The
gravitational field due to a mass distribution is 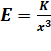 . in the
. in the 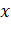 -direction.
(K is a constant). Taking the
gravitational potential to be zero at infinity, its value at a distance
-direction.
(K is a constant). Taking the
gravitational potential to be zero at infinity, its value at a distance 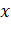 is
is
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: D
Gravitational potential = ![]()
= ![]()
= ![]()
= ![]()
= ![]()
31. The mass
of the earth is 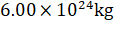 and
that of the moon is
and
that of the moon is 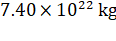 . The constant of gravitation
. The constant of gravitation 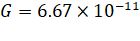 N-m2/kg2. The
potential energy of the system is
N-m2/kg2. The
potential energy of the system is  . The mean
distance between the earth and moon is
. The mean
distance between the earth and moon is
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: A
![]()
![]()
![]()
32. The kinetic
energy needed to project a body of mass m
from the earth surface (radius 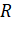 ) to
infinity is
) to
infinity is
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: C
![]() =
= ![]()
33. The escape velocity for a rocket from earth is 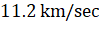 . Its
value on a planet where acceleration due to gravity is double that on the earth
and diameter of the planet is twice that of earth will be in
. Its
value on a planet where acceleration due to gravity is double that on the earth
and diameter of the planet is twice that of earth will be in 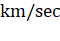
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: C
![]() =
= ![]()
= ![]()
= 2
![]() =
= ![]()
= ![]()
=![]()
34. The
escape velocity from the earth is about 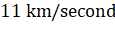 . The
escape velocity from a planet having twice the radius and the same mean density
as the earth
. The
escape velocity from a planet having twice the radius and the same mean density
as the earth
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: A
![]() =
= ![]()
= ![]()
![]() .
.
If r = constant Since the planet having double radius in comparison to earth therefore
the escape velocity becomes twice i.e. 22 km/s.
35. How much energy will be necessary for making a body of 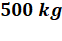 escape from the earth
escape from the earth 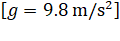 ,radius of
earth =
,radius of
earth = 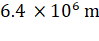 .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: C
Potential energy of a body at the surface of earth
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
So if we give this amount of energy in the form of kinetic
energy then body escape from the earth.
36. The escape velocity of an object on a planet whose 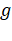 value is 9 times on earth and whose radius is
4 times that of earth in
value is 9 times on earth and whose radius is
4 times that of earth in 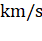 is
is
A) 67.2
B) 33.6
C) 16.8
D) 25.2
Solution: A
![]() =
= ![]()
= ![]()
= 6
![]() =
= ![]()
= ![]()
37. Given mass of
the moon is 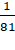 of the mass of the earth and corresponding
radius is
of the mass of the earth and corresponding
radius is 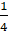 of the earth. If escape velocity on the earth
surface is
of the earth. If escape velocity on the earth
surface is 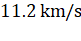 , the
value of same on the surface of the moon is
, the
value of same on the surface of the moon is
A) 0.14
km/s
B) 0.5 km/s
C) 2.5
km/s
D) 5
km/s
Solution: C
On earth ![]() =
= ![]()
= ![]()
On moon ![]() =
= ![]()
= ![]()
= ![]()
= ![]()
38. The
least velocity required to throw a body away from the surface of a planet so
that it may not return is (radius of the planet is 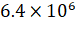 m,
m, 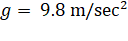 )
)
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: D
Escape
velocity from surface of earth
![]() =
= ![]()
= ![]()
= ![]()
39. Escape
velocity on earth is 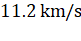 . What would
be the escape velocity on a planet whose mass is 1000 times and radius is 10
times that of earth?
. What would
be the escape velocity on a planet whose mass is 1000 times and radius is 10
times that of earth?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: A
![]() =
= ![]()
= ![]()
= 10
![]() =
= ![]()
= ![]()
40. Two
planets have the same average density but their radii are 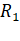 and
and 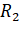 . If acceleration due to gravity on
these planets be
. If acceleration due to gravity on
these planets be 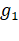 and
and 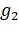 respectively, then
respectively, then
A) ![]()
B) ![]()
C) ![]()
D)![]()
Solution: A
![]()
If ![]() is
constant
is
constant ![]()
41. A body
weighs 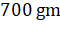 wt on the surface of the earth. How much will
it weigh on the surface of a planet whose mass is
wt on the surface of the earth. How much will
it weigh on the surface of a planet whose mass is 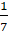 and
radius is half that of the earth?
and
radius is half that of the earth?
A) ![]()
B) ![]()
C) ![]()
D)![]()
Solution: B
We know that g
=![]() .
.
On the planet ![]() =
= ![]()
= ![]()
= ![]()
Hence weight on the planet
= 700 × ![]()
= ![]()
42. A
spherical planet far out in space has a mass 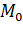 and diameter
and diameter 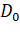 . A particle
of mass
. A particle
of mass 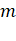 falling freely near the surface of this planet
will experience an acceleration due to gravity which is equal to
falling freely near the surface of this planet
will experience an acceleration due to gravity which is equal to
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: C
g
=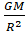
=
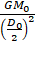
=
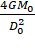
43. The mass
and diameter of a planet have twice the value of the corresponding parameters
of earth. Acceleration due to gravity on the surface of the planet is
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: B
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
44. The
radius of the earth is 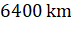 and
and 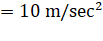 . In order that a body of
. In order that a body of 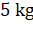 weighs zero at the equator, the angular speed
of the earth is
weighs zero at the equator, the angular speed
of the earth is
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Solution: C
For the
condition of weightlessness at equator
![]() =
= ![]()
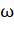 =
= 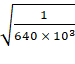
= 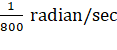
45. If 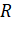 is the radius of the earth and g the acceleration due to gravity on the
earth's surface, the mean density of the earth is
is the radius of the earth and g the acceleration due to gravity on the
earth's surface, the mean density of the earth is
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: C
g = 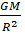 and M=
and M= 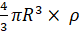
g = 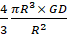
= 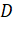
= 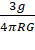
46. The mass of the earth is 81 times that
of the moon and the radius of the earth is 3.5 times that of the moon. The
ratio of the acceleration due to gravity at the surface of the moon to that at
the surface of the earth is
A) 0.15
B) 0.04
C) 1
D) 6
Solution: A
![]() (Given
(Given ![]() ,
, ![]() )
)
Substituting the above values,
![]()
47. The value of g on the earth's surface is 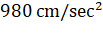 . Its
value at a height of 64 km from the earth's surface is
. Its
value at a height of 64 km from the earth's surface is
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: A
![]() =
= ![]()
= ![]()
= ![]()
=
![]()
48. At what
height over the earth's pole, the free fall acceleration decreases by one
percent (assume the radius of earth to be 6400 km).
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: A
![]()
![]()
![]()
If ![]() decrease by one percent then
decrease by one percent then ![]() should be increase by
should be increase by ![]()
i.e. R =![]()
= ![]()
49. At what
altitude in metre will the acceleration due to gravity be 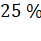 of that at the earth's surface (Radius of
earth =
of that at the earth's surface (Radius of
earth = 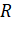 metre)
metre)
A) ![]()
B) ![]()
C) ![]()
D)
![]()
Solution: B
![]()
![]()
![]()
![]()
![]()