Huygens Principle

When we drop a small stone on a calm pool of water, waves spread out from the point of impact, starts oscillating with time forming circular rings on which the disturbance is maximum. Clearly, all points on such a circle are oscillating in phase because they are at the same distance from the source. Such a locus of points, which oscillate in phase is called a wavefront; thus a wavefront is defined as a surface of constant phase. The speed with which the wavefront moves outwards from the source is called the speed of the wave. The energy of the wave travels in a direction perpendicular to the wavefront.

If we have a point source emitting waves uniformly in all directions, then the locus of points which have the same amplitude and vibrate in the same phase are spheres and we have what is known as a spherical wave as shown in Figure below.

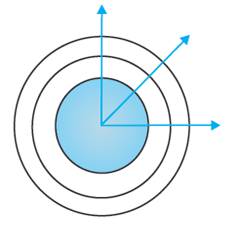
At a large distance from the source, a small portion of the sphere can be considered as a plane and we have what is known as a plane wave. This is shown in the figure given below.

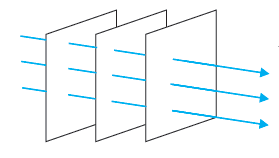
Now, if we know the shape of the wavefront at t = 0, then Huygens principle allows us to determine the shape of the wavefront at a later time t. Thus, Huygens principle is essentially a geometrical construction, which given the shape of the wafefront at any time allows us to determine the shape of the wavefront at a later time.

Let us consider a diverging wave and let F₁F₂ represent a portion of the spherical wavefront at t = 0 as shown in the below figure.

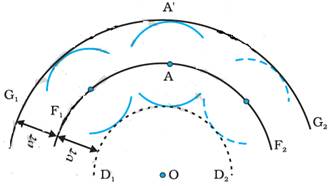
Now, according to Huygens principle, each point of the wavefront is the source of a secondary disturbance and the wavelets emanating from these points spread out in all directions with the speed of the wave. These wavelets emanating from the wavefront are usually referred to as secondary wavelets and if we draw a common tangent to all these spheres, we obtain the new position of the wavefront at a later time.

Characteristics of Waves

Amplitude:

Amplitude is the maximum displacement of the elements of the medium from their equilibrium positions as wave passes through them. It is denoted by A.

Phase:

Phase of a wave describes the state of motion as the wave sweeps through an element at a position.

Wavelength:

Wavelength is defined as the minimum distance between two consecutive crests or two consecutive troughs when in the same phase. It is denoted by λ.

Time Period of a wave:

Time Period of a wave is the time taken through one complete oscillation. It is denoted by ’T’.

Frequency of a wave:

Frequency of a wave is defined as number of oscillations per unit time. It is denoted by ν.

ν=1/T.