Work, Power And Energy

Work

The definition of work done may vary in real life and scientifically. For Example, We may consider studying, talking, singing, reading as work but it is not so in the case of science.

Examples of Scientific Work Done are:

· Moving a chair from one location to another

· Lifting a book from the shelf and placing it on a table

· Pushing a pebble lying on the ground.

In all these situations we are applying a force on an object which is then changing the state of rest or motion of the object.

So, we can conclude that work is done if and only if:

· A force is applied to an object.

· If the object is displaced from one point to another point.

These are also called ‘Conditions of Work Done’.

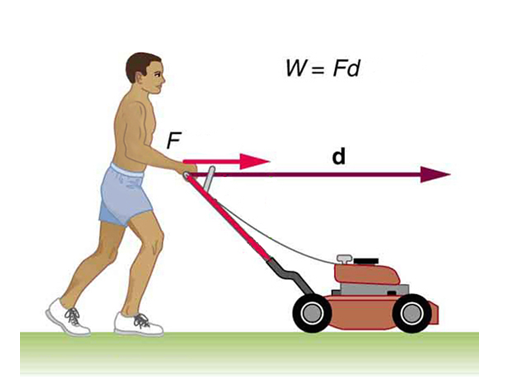
When you play a certain force ‘F Newton’ on an object and the object moves a distance of ‘ d meters’ in the direction where you applied the force then, the amount of work done can be calculated as:

Work done = Force * Displacement

W = F * d

Definition of Work Done: Work is defined as the product of the force applied on an object and displacement caused due to the applied force in the direction of the force. Work is a scalar quantity. It has no direction of its own but a magnitude.

SI unit of Work: N-m or J (Joule)

What is 1 Joule Work?

A situation where 1 Newton force is applied on an object that can move the object by a distance of 1m in the direction of the applied force, then 1 joule of work is said to be done.

· Depending upon the direction of displacement and force applied the nature of work done may vary. Consider the table given below:

The direction of Displacement	Work Done	Nature of Work Done	Angle between Force applied and Displacement occurred
Same as the direction of Force	W = F * d	Positive	0^o  (Force and Displacement are Parallel to each other)
Opposite as direction of Force	W = -F * d	Negative	180^o
No change in position	W = F * 0 = 0	Zero	90^o
Positive Work Done
Negative Work Done
Zero Work Done

Energy

Any object that is capable of doing work processes some energy. The object can gain or lose energy depending upon the work done. If an object does some work it loses its energy and if some work is done on an object it gains energy.

Different forms of energies

Kinetic Energy

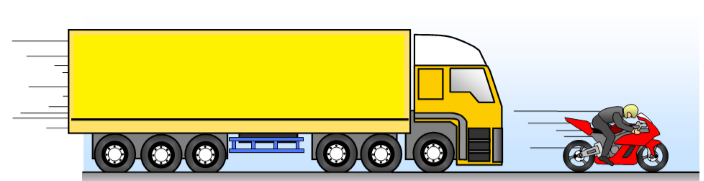
Every moving object possesses some energy called Kinetic Energy. As the speed of the object increases so is its kinetic energy.

Formula for Kinetic Energy

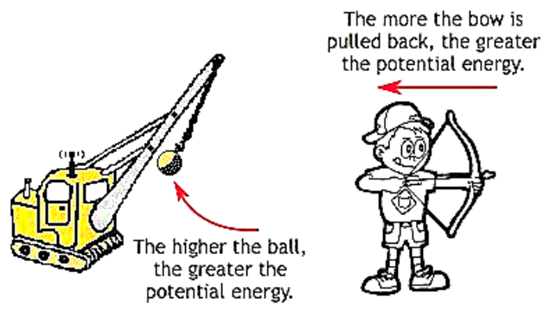
Potential Energy

Every object possesses some energy called Potential Energy. An object when gains energy may store it in itself as potential energy.

We know that when an object rises above the ground some work is done against gravity. Since work is done on the object, the object would gain some energy. The energy that the object gains at a height is called Gravitational Potential Energy. It is defined as the amount of work done required in raising an object above the ground up to a certain point against the gravity

Consider the example given below,

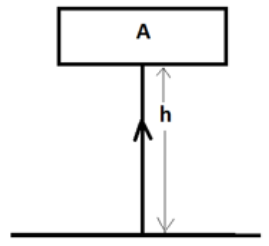
An object ‘A’ having mass ‘m’ is raised by height ‘h’ above the ground. Let us calculate the potential energy of object A at height ‘h’:

We know that,

W = F * d = F * h (height)

And F = m * g (because the force is applied against gravity)

So, W = m * g * h

Hence potential energy of object A, Ep = m * g * h

· Gravitational potential energy does not get affected due to the path taken by the object to reach a certain height.

Other forms of Energies:

· Mechanical Energy – It is the sum of kinetic and potential energy of an object. Therefore, it is the energy obtained by an object due to motion or by the virtue of its location. Example, a bicycle climbing a hill possesses kinetic energy as well as potential energy.

· Heat Energy – It is the energy obtained by an object due to its temperature. It is also called Thermal Energy. Example, energy possessed by a hot cup.

· Chemical Energy – It is the energy accumulated in the bonds of chemical compounds. Chemical energy is released at the time of chemical reactions. Example, energy possessed by natural gas and biomass.

· Electrical Energy – It is kind of kinetic energy caused due to the motion of electrons. It depends upon the speed of electrons. As the speed increases so does the electrical energy. Example, electricity produced by a battery, lightning at thunderstorms

· Light Energy – It is the energy due to light or electromagnetic waves. It is also called as Radiant Energy or Electromagnetic Energy. Example, energy from the sun

· Nuclear Energy – It is the energy present in the nucleus of an atom. Nuclear energy releases when the nucleus combines or separate. Therefore, we can say that every atom in this universe comprises of nucleus energy. Example, uranium is a radioactive metal capable of producing nuclear energy in nuclear power plants

· Sonic Energy – It is the energy produced by a substance as it vibrates. This energy flows through the substance in the form of sound waves. Example, music instruments produce sound energy

· Ionization Energy – It is the energy that binds electrons with its nucleus. It is thus the amount of energy required to remove one electron completely from its atom (called First Ionization Energy). Subsequently, the ionization energy increases as we remove the second electron from the atom ( called Second Ionization Energy).

- One form of energy can be transformed into other forms of energy.

Law of Conservation of Energy

According to the law of conservation of energy, the total amount of energy before and after transformation remains the same.

Consider the following example where an object of mass ‘m’ is made to fall freely from a height ‘h’.

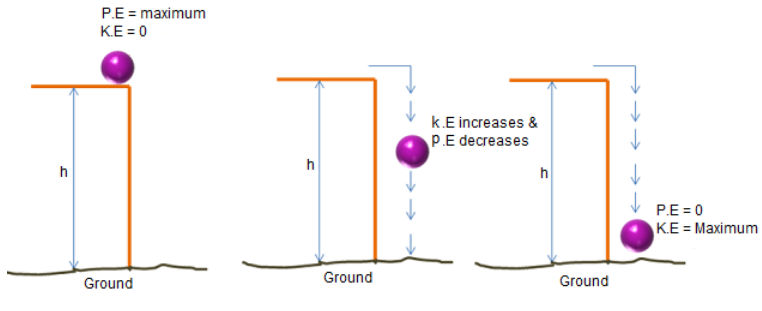
Instant	Height at an instant	Kinetic Energy	Potential Energy	Sum of KE + PE = ME
1	Height = h	0 (velocity is 0)	mgh	0 + mgh
2	Height = k	(1/2) mv1^2 (velocity = v1)	mgk	(1/2) mv1^2+ mgk
3	Height = 0	(1/2) mv2^2 (velocity = v2)	0	(1/2) mv2^2 + 0

We can see that the sum of kinetic energy and potential energy at every instant is constant. Hence, we can say the energy is conserved during transformation.

Power – The rate of doing work is defined as Power.

Power = Work Done / Time

P = W/ t

SI Unit: W (Watt) or J/s

1 kilowatt = 1000 watts

1 kW = 1000 W

1 W = 1000 J s^-1

Average Power = Total Energy Consumed / Total Time taken

Commercial Unit of Power

We cannot use Joule to measure power commercially. Instead, we use kilowatt-hour (kWh).

Commercial unit of energy = 1 kilowatt hour (kwh)

∴ 1 kWh = 1 kilowatt × 1 hour

= 1000 watt × 3600 seconds

= 3600000 Joule (watt × second)

1 kWh = 3.6 × 10⁶ J.

∴ 1 kWh = 1 unit

The energy used in one hour at the rate of 1 kW is called 1 kWh.