Motion

· A Reference Point is used to describe the location of an object. An object can be referred through many reference points.

· Origin – The reference point that is used to describe the location of an object is called Origin.

· For Example, a new restaurant is opening shortly at a distance of 5 km north from my house. Here, the house is the reference point that is used for describing where the restaurant is located.

What is motion?

If the location of an object changes with time the object is said to be in motion.

Motion in a Straight Line

Distance – The distance covered by an object is described as the total path length covered by an object between two endpoints.

Distance is a numerical quantity. We do not mention the direction in which an object is travelling while mentioning about the distance covered by that object.

Figure 1 – Distance and Displacement

According to the figure 1 given above, if an object moves from point O to point A then total distance travelled by the object is given as 60 km.

Displacement – The shortest possible distance between the initial and final position of an object is called Displacement.

Consider the figure 1 given above, here the shortest distance between O and A is 60 km only. Hence, displacement is 60 km.

Displacement depends upon the direction in which the object is travelling.

Displacement is denoted by Δx.

Δx = x_f − x₀

Where,

x_f = Final position on the object

x₀ = Initial position of the object

Zero Displacement – When the first and last positions of an object are same, the displacement is zero.

For Example, consider the diagrams given below.

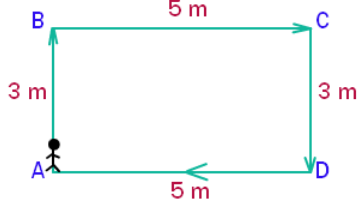
Figure 2 – Example for zero displacement

Displacement at point A = 0 because the shortest distance from A to A is zero.

Negative Displacement and Positive Displacement

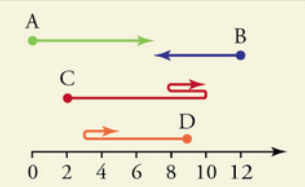
Figure 3 – Example for negative and positive displacement

Here, displacement of object B is negative

ΔB = B_f − B₀ = 7–12 = – 5

A negative sign indicates opposite direction here.

Also, displacement of object A is positive

ΔA = A_f − A₀ = 7– 0 = 7

What are Scalar and Vector Quantities?

· A scalar quantity describes a magnitude or a numerical value.

· A vector quantity describes the magnitude as well as the direction.

· Hence, distance is a scalar quantity while displacement is a vector quantity.

How is distance different from displacement?

Distance	Displacement
Distance provides the complete details of the path taken by the object	Displacement does not  provide the complete details of the path taken by the object
Distance is always positive	Displacement can be positive, negative or zero
It is a scalar quantity	It is a vector quantity
The distance between two points may not be unique	Displacement between two points is always unique

What is uniform motion?

When an object travels equal distances in equal intervals of time the object is said to have a uniform motion.

What is non-uniform motion?

When an object travels unequal distances in equal intervals of time the object is said to have a non-uniform motion.

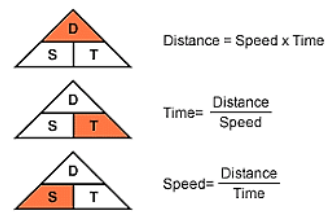
· Speed of an object is defined as the distance traveled by the object per unit time. 

SI Unit: Meter (m)

Symbol of Representation: m/s or ms^-1

Speed = Distance/Time

· Average Speed – If the motion of the object is non-uniform then we calculate the average speed to signify the rate of motion of that object.

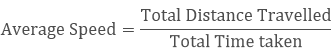
For Example, If an object travels 10m in 3 seconds and 12m in 7 seconds. Then its average speed would be:

Total distance travelled = 10 m + 12 m = 22m

Total Time taken = 3s + 7s = 10s

Average speed = 22/10 = 2.2 m/s

· To describe the rate of motion in a direction the term velocity is used. It is defined as the speed of an object in a particular direction.

Velocity = Displacement/Time

SI Unit: Meter (m)

Symbol of Representation: M/s or ms^-1

Average Velocity (in case of uniform motion)-

Average Velocity = (Initial Velocity + Final Velocity)/2

Average Velocity (in case of non-uniform motion)-

Average Velocity = Total Displacement / Total Time taken

What are instantaneous speed and instantaneous velocity?

The magnitude of speed or velocity at a particular instance of time is called Instantaneous Speed or Velocity.

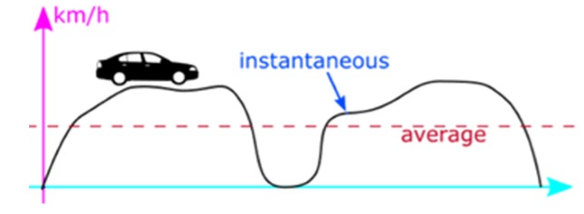
Figure 4 - Instantaneous Speed / Velocity 

Uniform Motion – In case of uniform motion the velocity of an object remains constant with change in time. Hence, the rate of change of velocity is said to be zero.

Non-uniform Motion – In case of non-uniform motion the velocity of an object changes with time. This rate of change of velocity per unit time is called Acceleration.

Acceleration = Change in velocity/ Time taken

SI Unit: m/s²

Uniform Acceleration – An object is said to have a uniform acceleration if:

· It travels along a straight path 

· Its velocity changes (increases or decreases) by equal amounts in equal time intervals

Non - Uniform Acceleration – An object is said to have a non-uniform acceleration if:

· Its velocity changes (increases or decreases) by unequal amounts in unequal time intervals

Acceleration is also a vector quantity. The direction of acceleration is the same if the velocity is increasing in the same direction. Such acceleration is called Positive Acceleration.

The direction of acceleration becomes opposite as that of velocity if velocity is decreasing in a direction. Such acceleration is called Negative Acceleration.

De-acceleration or Retardation – Negative acceleration is also called De-acceleration or Retardation

Graphical Representation of Motion

1. Distance – Time Graph

It represents a change in position of the object with respect to time.

The graph in case the object is stationary (means the distance is constant at all time intervals) – Straight line graph parallel to x = axis

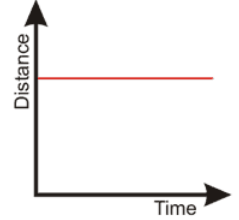
Figure 5 - Distance-time Graph in case of Stationary object

The graph in case of uniform motion – Straight line graph

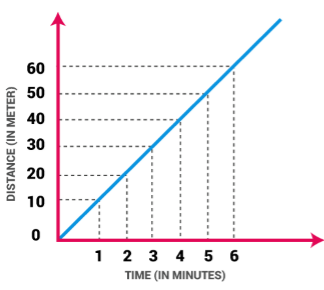
Figure 6 - Distance-time Graph in Uniform Motion

The graph in case of non-uniform motion – Graph has different shapes

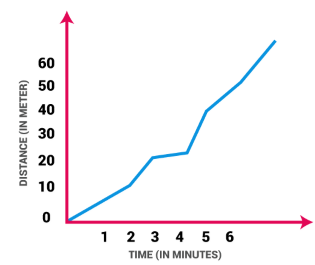
Figure 7- Distance-time Graph in Non-Uniform Motion 

2. Velocity – Time Graphs

Constant velocity – Straight line graph, velocity is always parallel to the x-axis

Uniform Velocity / Uniform Acceleration – Straight line graph

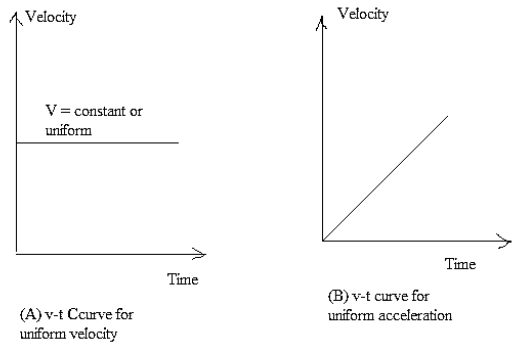
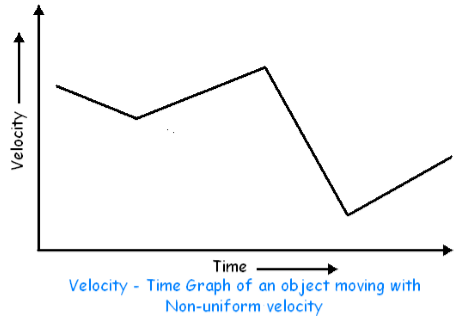
Non-Uniform Velocity / Non-Uniform Acceleration – Graph can have different shapes

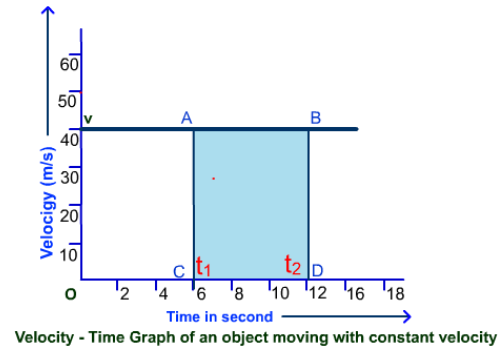
Calculating Displacement from a Velocity-time Graph

Consider the graph given below. The area under the graph gives the distance traveled between a certain interval of time. Hence, if we want to find out the distance traveled between time interval t₁ and t₂, we need to calculate the area enclosed by the rectangle ABCD where area (ABCD) = AB * AC.

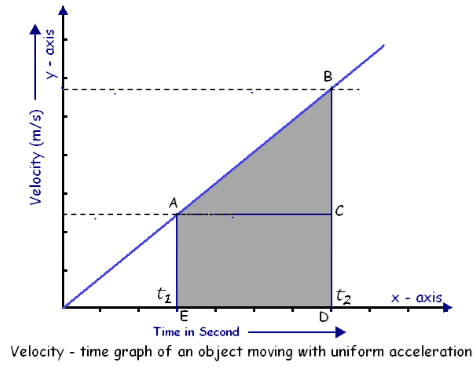
Similarly, to calculate distance traveled in a time interval in case of uniform acceleration, we need to find out the area under the graph, as shown in the figure below.

To calculate the distance between time intervals t₁ and t₂ we need to find out area represented by ABED.

Area of ABED = Area of the rectangle ABCD + Area of the triangle ADE = AB × BC + 1/ 2 * (AD × DE)

Equations of Motion

The equations of motion represent the relationship between an object's acceleration, velocity and distance covered if and only if,

· The object is moving on a straight path

· The object has a uniform acceleration

Three Equations of Motion

1. The Equation for Velocity – Time Relation

v = u + at

2. The Equation for Position – Time Relation 

s = ut + 1/2 at²

3. The Equation for the Position – Velocity Relation

2a s = v² – u²

Where,

u: initial velocity

a: uniform acceleration

t: time

v: final velocity

s: distance traveled in time t

Deriving the Equations of Motion Graphically

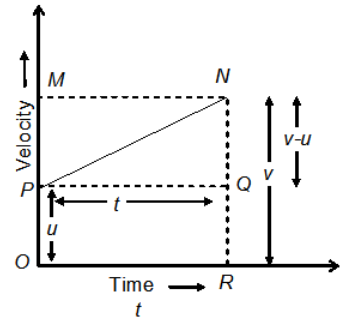
Figure 12

Study the graph above. The line segment PN shows the relation between velocity and time. 

Initial velocity, u can be derived from velocity at point P or by the line segment OP

Final velocity, v can be derived from velocity at point N or by the line segment NR

Also, NQ = NR – PO = v – u

Time interval, t is represented by OR, where OR = PQ = MN

1. Deriving the Equation for Velocity – Time Relation

Acceleration = Change in velocity / time taken

Acceleration = (final velocity – initial velocity) / time

a = (v – u)/t

so, at = v – u

v = u + at

2. Deriving Equation for Position – Time Relation

We know that, distance travelled by an object = Area under the graph

So, Distance travelled = Area of OPNR = Area of rectangle OPQR + Area of triangle PQN

s = (OP * OR) + (PQ * QN) / 2

s = (u * t) + (t * (v – u) / 2)

s = ut + 1/2 at²           [because at = v – u]

3. Deriving the Equation for Position – Velocity Relation

We know that, distance travelled by an object = area under the graph

So, s = Area of OPNR = (Sum of parallel sides * height) / 2

 s = ((PO + NR)* PQ)/ 2 = ( (v+u) * t)/ 2

2s / (v+u) = t [equation 1]

Also, we know that, (v – u)/ a = t [equation 2]

On equating equations 1 and 2, we get,

2s / (v + u) = (v – u)/ a

2as = (v + u) (v – u) 

2 a s = v² – u²

Uniform Circular Motion

If an object moves in a constant velocity along a circular path, the change in velocity occurs due to the change in direction. Therefore, this is an accelerated motion. Consider the figure given below and observe how directions of an object vary at different locations on a circular path.

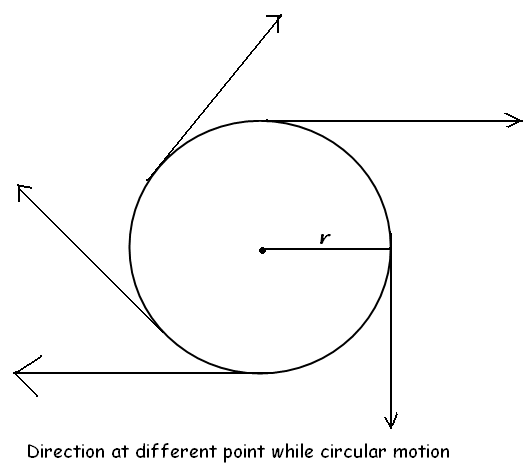
Uniform Circular Motion – When an object travels in a circular path at a uniform speed the object is said to have a uniform circular motion.

Non-Uniform Circular Motion – When an object travels in a circular path at a non-uniform speed the object is said to have a non-uniform circular motion

Examples of uniform circular motion:

· The motion of a satellite in its orbit

· The motion of planets around the sun

Velocity of Uniform Circular Motion

Velocity = Distance/ Time = Circumference of circle / Time

v = 2πr/ t

where,

v: velocity of the object

r: radius of the circular path

t: time taken by the object