ACOUSTICS
INTRODUCTION
Sound
plays a major role in our lives. We communicate with each other mainly through
sound. In our daily life, we hear a variety of sounds produced by different
sources like humans, animals, vehicle horns, etc. Hence, it becomes inevitable
to understand how sound is produced, how it is propagated and how you hear the
sound from various sources. It is sometimes misinterpreted that acoustics only
deals with musical instruments and design of auditoria and concert halls. But,
acoustics is a branch of physics that deals with production, transmission,
reception, control, and effects of sound. You have studied about propagation
and properties of sound waves in IX standard. In this lesson we will study
about reflection of sound waves, Echo and Doppler effect.
SOUND WAVES
When
you think about sound, the questions that arise in your minds are: How is sound
produced? How does sound reach our ears from various sources? What i
Suppose
you and your friend are on the Moon. Will you be able to hear any sound
produced by your friend? As the Moon does not have air, you will not be able to
hear any sound produced by your friend. Hence, you understand that the sound
produced due to the vibration of different bodies needs a material medium like
air, water, steel, etc, for its propagation. Hence, sound can propagate through
a gaseous medium or a liquid medium or a solid medium.
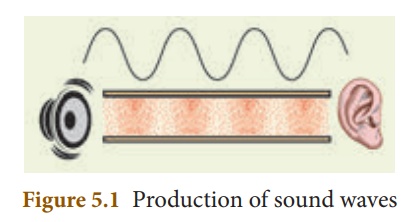
1. Longitudinal Waves
Sound
waves are longitudinal waves that can travel through any medium (solids,
liquids, gases) with a speed that depends on the properties of the medium. As
sound travels through a medium, the particles of the medium vibrate along the
direction of propagation of the wave. This displacement involves the
longitudinal displacements of the individual molecules from their mean positions.
This results in a series of high and low pressure regions called compressions
and rarefactions as shown in figure
![]()
2. Categories of sound
waves based on their frequencies
(i)
Audible waves –
These are sound waves with a frequency ranging between 20 Hz and
20,000 Hz. These are generated by vibrating bodies such as vocal cords,
stretched strings etc.
(ii) Infrasonic waves –
These are sound waves with a frequency below 20 Hz that cannot be
heard by the human ear. e.g., waves produced during earth quake, ocean waves,
sound produced by whales, etc.
(iii) Ultrasonic
waves – These
are sound waves with a frequency greater than 20 kHz, Human ear
cannot detect these waves, but certain creatures like mosquito, dogs, bats,
dolphins can detect these waves. e.g., waves produced by bats.
4. Velocity of sound waves
When
you talk about the velocity associated with any wave, there are two velocities,
namely particle velocity and wave velocity. SI unit of velocity is metre (m)
Particle velocity:
The
velocity with which the particles of the medium vibrate in order to transfer
the energy in the form of a wave is called particle velocity.
Wave velocity:
The
velocity with which the wave travels through the medium is called wave
velocity. In other words, the distance travelled by a sound wave in unit time
is called the velocity of a sound wave.
∴ Velocity = Distance / Time taken
If
the distance travelled by one wave is taken as one wavelength (λ) and, the
time taken for this propagation is one time period (T), then, the expression
for velocity can be written as
∴ V = λ/T (5.1)
Therefore,
velocity can be defined as the distance travelled per second by a sound wave.
Since, Frequency (n) =1/T, equation (5.1) can be written as
V = nλ (5.2)
Velocity
of a sound wave is maximum in solids because they are more elastic in nature
than liquids and gases. Since, gases are least elastic in nature, the velocity
of sound is the least in a gaseous medium.
So, vS >
vL > vG
5. Factors affecting velocity of sound
In
the case of solids, the elastic properties and the density of the solids affect
the velocity of sound waves. Elastic property of solids is characterized by
their elastic module.
The speed of sound is directly proportional to the square root of the elastic
modulus and inversely proportional to the square root of the density. Thus the
velocity of sound in solids decreases as the density increases whereas the
velocity of sound increases when the elasticity of the material increases. In
the case of gases, the following factors affect the velocity of sound waves.
Effect of density:
The
velocity of sound in a gas is inversely proportional to the square
root of the density of the gas. Hence, the velocity decreases as the density of
the gas increases.
Effect of
temperature:
The
velocity of sound in a gas is directly proportional to the square root of its
temperature. The velocity of sound in a gas increases with the increase in
temperature. v ∝ √T.
Velocity at temperature T is given by the following equation:
vT =
(vo + 0.61 T) m s–1
Here,
vo is the
velocity of sound in the gas at 0° C. For air, vo = 331 m s–1.
Hence, the velocity of sound changes by 0.61 m s–1 when the
temperature changes by one degree celsius.
Effect of relative
humidity:
When
humidity increases, the speed of sound increases. That is why you
can hear sound from long distances clearly during rainy seasons.
Speed
of sound waves in different media are given
SOUND:
Reflection of Sound
Sound wave also gets reflected as light waves
do. Bouncing back of sound wave from the surface of solid or liquid is called
reflection of sound.
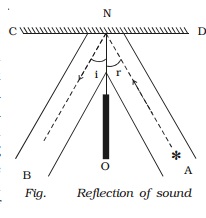
Reflection
of sound follows the Laws of Reflection as light wave does. This means the
angle of incident wave and reflected wave to the normal are equal.
For
reflection of sound a polished or rough and big obstacle is necessary.
Use of Reflection of Sound:
Reflection of sound is used in many devices.
For example; megaphone, loudspeaker, bulb horn, stethoscope, hearing aid, sound
board etc.
Applications of reflection of
sound waves
Applications
of reflection of sound waves - Whispering gallery, Stethoscope
, Echo.
Applications of
reflection of sound waves
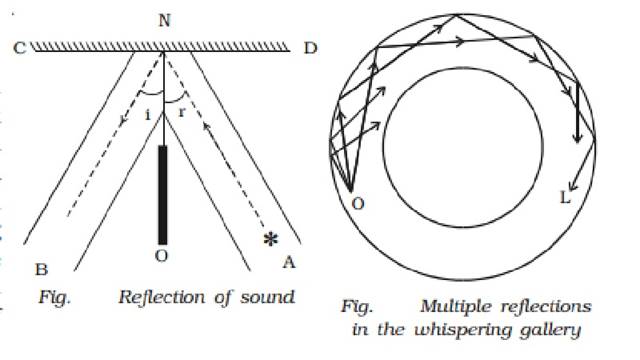
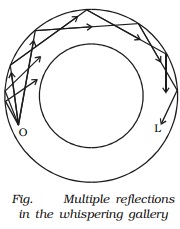
(i) Whispering gallery : The
famous whispering gallery at St. Paul?s Cathedral is
a circular shaped chamber whose walls repeatedly reflect sound waves round the
gallery, so that a person talking quietly at one end can be heard distinctly at
the other end. This is due to multiple reflections of sound waves from the
curved walls (Fig.).
(ii) Stethoscope : Stethoscope
is an instrument used by physicians to listen to the sounds produced by various
parts of the body. It consists of a long tube made of rubber or metal. When
sound pulses pass through one end of the tube, the pulses get concentrated to
the other end due to several reflections on the inner surface of the tube.
Using this doctors hear the patients? heart beat as
concentrated rays.
(iii) Echo :
Echoes
are sound waves reflected from a reflecting surface at a distance from the
listener. Due to persistence of hearing, we keep hearing the sound for 1 /10th
of a second, even after the sounding source has stopped vibrating. Assuming the
velocity of sound as 340 ms?1, if the sound reaches the obstacle and returns
after 0.1 second, the total distance covered is 34 m. No echo is heard if the
reflecting obstacle is less than 17 m away from the source.
DOPPLER
EFFECT :
Different cases and Applications
The whistle of a fast moving train appears to
increase in pitch as it approaches a stationary observer and it appears to
decrease as the train moves away from the observer.
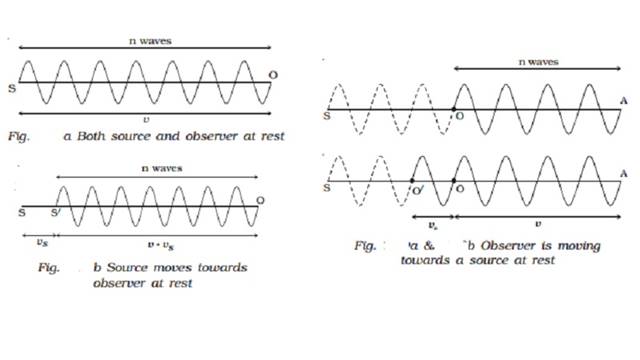
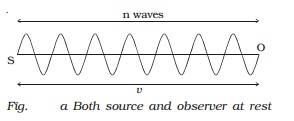
(i) Both source and
observer at rest
Suppose S and O are the positions of
the source and the observer respectively. Let n be the frequency of the sound
and v be the velocity of sound. In one second, n waves produced by the source
travel a distance SO = v (Fig. a).
The
wavelength is λ = v/n
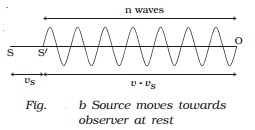
(ii) When the source
moves towards the stationary observer
If the source moves with a velocity vs towards
the stationary observer, then after one second, the source will reach S′,
such that SS′ = vs. Now n waves emitted by the source will
occupy a distance
of
(v?vs) only as shown in Fig. b.
Therefore
the apparent wavelength of the sound is
λ = (v-vs)/n
The
apparent frequency
n?
= v/ λ? = (v/v-vs)n ????..(1)
As
n′ > n, the pitch of the sound appears to increase.
When
the source moves away from the stationary observer
If
the source moves away from the stationary observer with velocity vs, the
apparent frequency will be given by
n?
= (v/[v-(-vs)])n = (v/[v+vs])n
????.(2)
As
n′ < n, the pitch of the sound appears to decrease.
(iii) Source is at rest
and observer in motion
S and O represent the positions of
source and observer respectively.
The
source S emits n waves per second having a wavelength λ = v/ n .
Consider
a point A such that OA contains n waves which crosses the ear of the observer
in one second (Fig. a). (i.e) when the first wave is
at the point A, the nth wave will be at O, where the observer is situated.
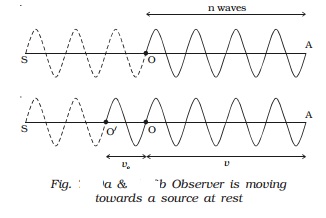
When the observer moves towards the stationary source
Suppose
the observer is moving towards the stationary source with velocity vo. After one second the observer will reach the
point O′ such that OO′ = vo.
The number of waves crossing the observer will be n waves in the distance OA in
addition to the number of waves in the distance OO′ which is equal to vo/λ as shown in Fig. b.
Therefore,
the apparent frequency of sound is
n′
= n + vo/ λ = n +(v0/v)n
∴ n′
= ((v+v0)/v)n ???..(3)
As
n′ > n, the pitch of the sound appears to increase.
When
the observer moves away from the stationary source
n′
= [v +(-v0)/v]n
n′
= ( v-vo / v
)n
As
n′ < n, the pitch of sound appears to decrease.
Note :
If the source and the observer move along the same
direction,
the equation for apparent frequency is
n′ = (v-v0 / v-vs )n
Suppose
the wind is moving with a velocity W in the direction of propagation of sound,
the apparent frequency is
n′
= ([v+W-v0]/ [v+W-vs])n
Applications of Doppler effect
(i)
To measure the speed of an automobile
An
electromagnetic wave is emitted by a source attached to a police car. The wave
is reflected by a moving vechicle, which acts as a
moving source. There is a shift in the frequency of the reflected wave. From
the frequency shift using beats, the speeding vehicles are trapped by the
police.
(ii) Tracking
a satellite
The
frequency of radio waves emitted by a satellite decreases as the satellite
passes away from the Earth. The frequency received by the Earth station,
combined with a constant frequency generated in the station gives the beat
frequency. Using this, a satellite is tracked.
(iii) RADAR
(RADIO DETECTION AND RANGING)
A
RADAR sends high frequency radio waves
towards an aero plane. The reflected waves are detected by the receiver of the
radar station. The difference in frequency is used to determine the speed of an
aero plane.
(iv) SONAR
(SOUND NAVIGATION AND RANGING)
Sound waves generated from a ship
fitted with SONAR are transmitted in water towards an approaching submarine.
The frequency of the reflected waves is measured and hence the speed of the
submarine is calculated.