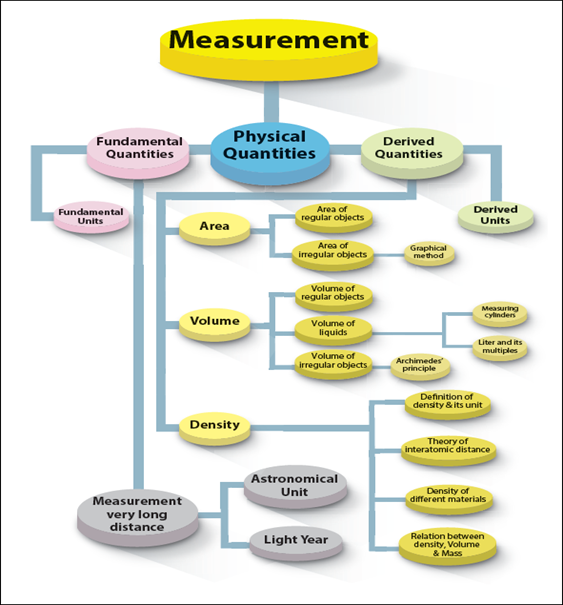
Measurement
A value and a unit are used to express and
measure the magnitude of a physical quantity.
For
example Suresh walks 2 kilometre every day. In this example ‘2’ is the value
and ‘kilometre’ is the unit used to express the magnitude of distance which is
a physical quantity.
1.
Fundamental
and derived quantities:
Generally, physical quantities are classified
into two types, namely,
(i)
Fundamental
quantities
(ii)
Derived
quantities.
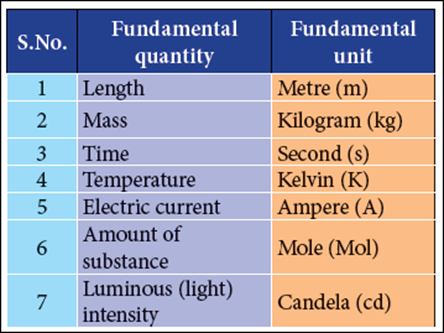
Fundamental
quantities:
A
set of physical quantities which cannot be expressed in terms of any other
quantities are known as “Fundamental quantities”. Their corresponding units are
called “Fundamental units”.
There are seven
fundamental physical quantities in SI Units (System of International Units).
Derived
quantities:
All other physical
quantities which can be obtained by multiplying, dividing or by mathematically
combining the fundamental quantities are known as “derived quantities”.
Their corresponding units are called “Derived units”.
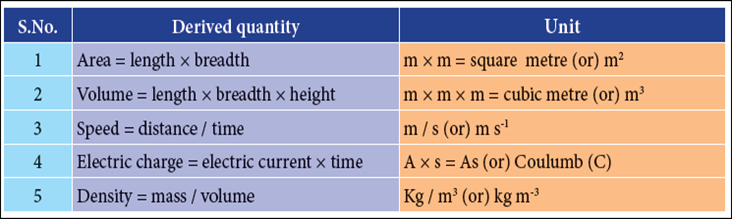
Area:
The area is a measure of how much
space there is on a flat surface.
The area of the plot of
land is derived by multiplying the length and breadth
Area = length × breadth
The unit of the area is
= meter × meter
= metre2
= m2
(Read as square meter).
Area
is a derived quantity as we obtain are by multiplying twice of the fundamental
physical quantity length.
One
square meter is the area enclosed inside a square of side 1 meter.
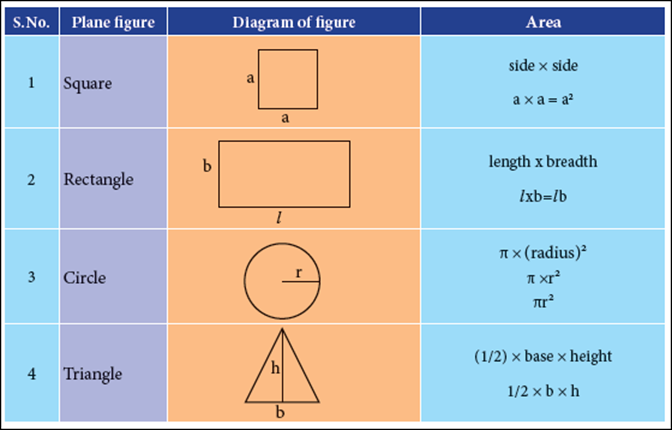
Area of
regularly shaped figures
The area of regularly shaped figures
can be calculated using the relevant formulae.
Area of
irregularly shaped figures
 In our daily life, we encounter
many irregularly shaped figures like leaves, maps, stickers of stars or
flowers, peacock feather etc. The area of such irregularly shaped figures cannot
be calculated using any formula.
In our daily life, we encounter
many irregularly shaped figures like leaves, maps, stickers of stars or
flowers, peacock feather etc. The area of such irregularly shaped figures cannot
be calculated using any formula.
Volume
The amount of space
occupied by a three dimensional object is known as its volume.
Volume
= surface area × height
The SI unit of volume
is cubic meter or m3.
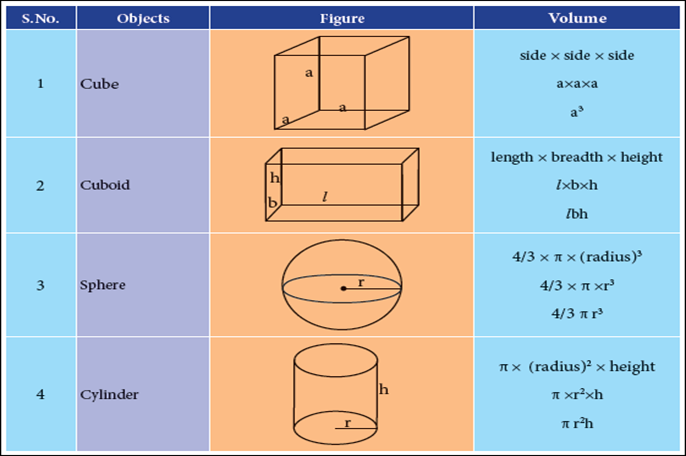
Volume of regularly shaped objects
As in the
case of area, the volume of the regularly shaped objects can also be determined
using an appropriate formula.
Volume of liquids
Liquids also occupy some space and hence they also have
volume. But, liquids do not possess any definite shape. So, the volume of a
liquid cannot be determined as in the case of solids. When a liquid is poured
into a container, it takes the shape and volume of the container. The volume of
any liquid is equal to the space that it fills and it can be measured using a
measuring cylinder or measuring beaker. The maximum volume of liquid that a
container can hold is known as the “capacity of the container”. A measuring
container is graduated.
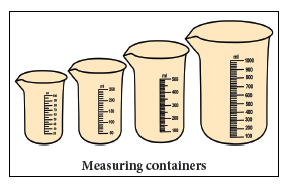
The volume of a liquid is equal to
the volume of space it fills in the container. This can be directly observed
from the readings marked in the measuring containers.
Liter
is the commonly used unit to measure the volume of liquids. We can understand
that the unit of volume is cubic cm if the dimensions of the object are given
in cm. This cubic cm is commonly known as cc. A volume of 1000 cc is termed as
one liter (l).
1
liter = 1000 cc or cm3
1000
ml = 1 liter
To measure the
volume of liquids, some other units are also used. Some of them are gallon,
ounce, and quart.
1 gallon = 3785 ml
1 ounce = 30 ml
1 quart = 1 liter
Volume of irregularly shaped objects
There are no formulae
to determine the volume of irregularly shaped objects. For such cases, their
volume can be determined using a measuring cylinder and water.
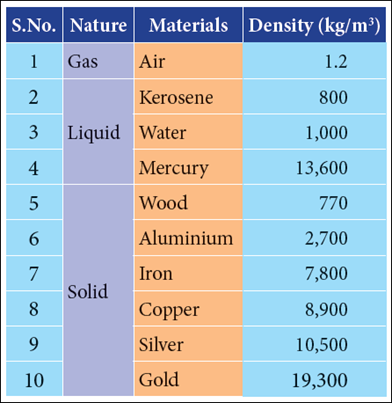
Density
Density of a substance is defined as
the mass of the substance contained in unit volume (1 m3).
If the mass of a substance is “M” whose volume is “V”,
then, the equation for density is given as
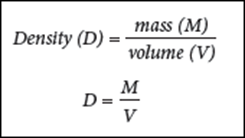
SI
unit of density is kg/m3.
The CGS unit of density is g/cm3.
Density
of different materials
Different materials have different
densities. The materials with higher density are called “denser” and the
materials with lower density are called “rarer”.
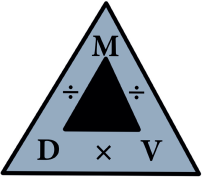
Relationship between Mass, Volume and Density
Density = Mass/ Volume
Mass = Density × Volume
Volume = Mass / Density
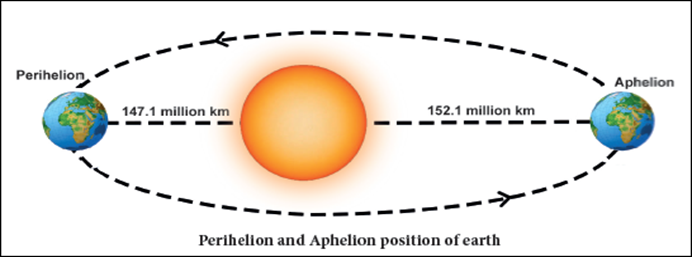
Measuring
distance of celestial bodies
Normally,
we use centimeter, meter and kilo meter to express the distances that we
measure in our day to day life. But, for space research, astronomers need to
measure very long distances such as the distance between the earth
and a star or the distance between two stars. To express these distances, we
shall learn about two such units, namely,
i. Astronomical unit
ii. Light
year
Astronomical Unit
One
astronomical unit is defined as the average distance between the earth and the
sun.
1
AU = 149.6 million km = 149.6 × 106 km = 1.496 × 1011 m.
Light
Year
One light year is defined as the
distance travelled by light in vacuum during the period of one year.
1
Light year = 9.46 × 1015 m.