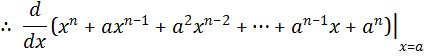Derivatives
Study Material:
Introduction:
The derivative of a
function of real variable ![]() measures the sensitivity to change of function
value with respect to change of its argument.
measures the sensitivity to change of function
value with respect to change of its argument.
 For
example, the derivative of the position of a moving
For
example, the derivative of the position of a moving
![]() Point with respect to time is the
velocity of that point.
Point with respect to time is the
velocity of that point.
Derivative
can be generalized to functions of several variables.
The
processing to find the derivative is called differentiation.
Definition:
Let ![]() be a real valued function and
be a real valued function and ![]() be any point on its domain. Then the
derivative of
be any point on its domain. Then the
derivative of ![]() at
at ![]() is denoted by
is denoted by ![]() and defined by
and defined by
![]() ,
provided this limit exists.
,
provided this limit exists.
Or
![]() ,
provided this limit exists.
,
provided this limit exists.
To find the derivative of ![]() at any arbitrary point
at any arbitrary point ![]() is given by
is given by
![]()
This
definition of derivative is also called the first principle of derivative.
Remark:
There are different
notations for derivative of a function. The derivative of ![]() ,
, ![]() is denoted by
is denoted by ![]() or
or ![]() or D
or D![]() . Also
the derivative of
. Also
the derivative of ![]() at the point
at the point ![]() is denoted by
is denoted by ![]() or
or 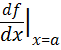
Example:
Find the derivative of ![]() at
arbitrary point
at
arbitrary point ![]()
Solution:

![]()
![]()
![]()
![]() .
.
Left hand derivative:
The left hand derivative
of a real valued function ![]() at
at ![]() is denoted by
is denoted by ![]() and is defined by,
and is defined by,
![]()
or
![]()
Right hand derivative:
The right
hand derivative of a real valued function ![]() at
at ![]() is denoted by
is denoted by ![]() and is defined by,
and is defined by,
![]()
or
![]()
Note:
The
derivative of a function exists if and only if its left hand derivative and
right hand derivative exist and equal that is ![]() exists if and only if
exists if and only if ![]() .
.
Example:
Find the left hand derivative and right hand derivative of the given function
at ![]()
![]()
Solution:
![]()
![]()
And ![]()
![]()
![]()
![]() .
.
Geometric representation of derivatives:
Let us consider a curve ![]() and draw a tangent of the curve at the point
and draw a tangent of the curve at the point ![]() which makes an angle
which makes an angle ![]() with the
with the ![]() - axis.
- axis.
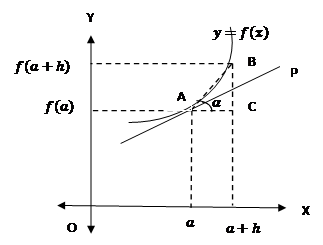 Let
Let ![]() be another point very close to the point
be another point very close to the point![]() . Add
the points A and B.
. Add
the points A and B.
Let
![]() .
.
Then from
the ![]() ABC,
ABC,
![]()
![]()
Now, from the figure we say that when B![]() A that
is when the point B moves toward the point A, then
A that
is when the point B moves toward the point A, then ![]() unboundedly decrease and approach to
unboundedly decrease and approach to ![]() and the line AB will approach to the tangent
AP. Then
and the line AB will approach to the tangent
AP. Then
![]()
i.e., ![]()
Algebra of derivative of functions:
Let ![]() and
and ![]() be two functions whose derivatives are defined
in a common domain. Then
be two functions whose derivatives are defined
in a common domain. Then
1. Derivative of sum of two functions is
the sum of the derivatives of that two functions. That is
![]()
2. Derivative of difference of
two functions is the difference of the derivatives of that two functions. That
is
![]()
3. Derivative of product of two
functions is the product of the derivatives of that two functions. That is
![]()
4. Derivative of quotient of
two functions is the quotient of the derivatives of that two functions
(whenever the denominator is non-zero). That is
 .
.
Note:
In
particular if we take![]() , where
, where
![]() is a constant then the formula 3 formed as
is a constant then the formula 3 formed as ![]()
Remark:
if
![]() and
and ![]() , then
the above equations can be written as
, then
the above equations can be written as
1.
![]()
2.
![]()
3.
![]()
4.
![]() Respectively.
Respectively.
Basic formulas of derivatives:
General
derivative formulas:
1. ![]() , where
, where
![]() is any constant.
is any constant.
2. ![]() , where
, where
![]() is positive or negative integer. This is
called power rule of derivatives. In particular if we take
is positive or negative integer. This is
called power rule of derivatives. In particular if we take ![]() , then
, then ![]() .
.
3. ![]() , where
, where
![]() is any function. This is called the power rule
for functions.
is any function. This is called the power rule
for functions.
Derivative
of logarithm functions:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Derivative
of exponential functions:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
Derivative
of trigonometric functions:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
Derivative
of hyperbolic functions:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
Derivative
of inverse trigonometric functions:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
Derivative
of hyperbolic functions:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]() .
.
Example
1: Prove that derivative of ![]() is
is ![]() .
.
Proof: Let ![]() then
then
![]()
![]()
![]()
![]() .
. 
![]() (Proved).
(Proved).
Example
2: Compute the derivative of ![]()
Solution:
![]()
![]()
![]() .
.
Solutions of the exercises of NCERT book
1.
Find the derivative of ![]() at
at ![]() .
.
Solution:
![]()
![]()
Therefore the
![]() .
.
2.
Find
the derivative of ![]() at
at ![]() .
.
Solution:
![]() .
.
So the
derivative of ![]() at
at ![]() is
is![]() .
.
3.
Find
the derivative of ![]() at
at![]() .
.
Solution:
![]()
![]() .
. ![]()
4.
Find the
derivative of the following functions from first principle.
i).![]()
Solution:
Let![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
ii) ![]()
Solution:
Let ![]() .
.
|
|
![]()
![]()
![]() .
.
iii). ![]()
Solution:
Let ![]()
|
|
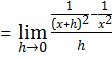
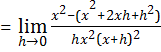
![]()
![]() .
.
iv) ![]()
Solution:
Let ![]()
|
|
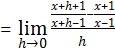
![]()
![]() .
.
5.
For the
function ![]() . Prove that
. Prove that ![]() .
.
Proof.
Here ![]()
![]()
|
So, |
![]()
And ![]() .
.
Hence ![]() .
.
6.
Find
the derivative of ![]() , for some real number
, for some real number ![]() .
.
Solution:
![]()
![]()
|
|
![]()
![]()
![]()
![]() .
.
7.
For
some constant ![]() and
and ![]() find
the derivative of
find
the derivative of
(i)
Solution:
![]()
![]()
![]()
(ii)
![]()
Solution:
![]()
![]()
![]()
(iii)
![]()
Solution:
![]()
![]()
8.
Find
the derivative of ![]() for
some constant
for
some constant![]() .
.
Solution:
![]()
![]()
![]()
So, ![]()
![]()
![]()
9.
Find
the derivative of
(i)
![]()
Solution:
![]()
![]() .
.
(ii)
![]()
Solution:
![]()
![]()
![]()
![]() .
.
(iii)
![]()
Solution:
![]()
![]()
![]() .
.
(iv)
![]()
Solution:
![]()
![]() .
.
(v)
Solution:
![]()
![]() .
.
(vi)
![]()
Solution:
![]()
![]()
![]()
10.
Find
the derivative of ![]() from
first principle.
from
first principle.
Solution:
Let
![]() then.
then.
|
|
![]()
![]()
![]() .
. 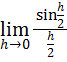
![]() .
.
11.
Find
the derivative of the following functions:
(i)
![]()
Solution:
![]()
![]() .
.
(ii)
![]()
Solution:
![]()
(iii)
![]()
Solution:
![]()
![]() .
.
(iv)
![]()
Solution:
![]() .
.
(v)
![]()
Solution:
![]()
![]() .
.
(vi)
![]()
Solution:
![]()
![]() .
.
(vii)
![]()
Solution:
![]()
![]() .
.