Limits
Study Material:
Definition:
Let ![]() be a real valued function and
be a real valued function and ![]() be a real number.
be a real number.
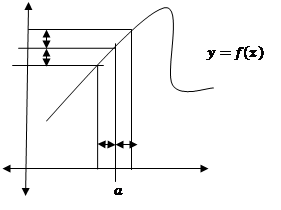
Then ![]() can made to be as closed to
can made to be as closed to ![]() as desired by making
as desired by making ![]() sufficiently closed to
sufficiently closed to ![]() , then
, then ![]() is said to be the limit of the function
is said to be the limit of the function ![]()
![]()
 And is
written as,
And is
written as, ![]() .
.
![]()
![]()
Example:
Let ![]()
Here
![]() is undefined but near to
is undefined but near to![]() , like
at
, like
at![]() ,
,![]() ,
,
![]() ,
, ![]() . That
is the value of
. That
is the value of ![]() approach to
approach to ![]() as
as ![]() approach to
approach to ![]() . So
here limit of
. So
here limit of ![]() is 2.
is 2.
Note:
There are
essentially two way to approach ![]() could approach a number
could approach a number![]() ,
either from left side of from right side.
,
either from left side of from right side.
Left hand limit:
The expected value of ![]() at
at ![]() when
when ![]() approaches to the left side of
approaches to the left side of ![]() is said to be the left hand limit of
is said to be the left hand limit of ![]() at
at![]() an is denoted
an is denoted
By
![]()
Right hand limit:
The expected value of ![]() at
at ![]() when
when ![]() approaches to the right side of
approaches to the right side of ![]() is said to be the right hand limit of
is said to be the right hand limit of ![]() at
at![]() an is denoted by
an is denoted by ![]() .
.
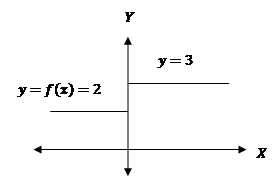 Example:
Example:
Let ![]()
Here left hand
limit ![]()
And right
hand limit ![]()
But ![]()
Note:
If the
left hand limit and right hand limit are equal and equal to ![]() , i.e.,
, i.e.,
![]() , then
, then
![]() .
.
Algebra of limits:
Let ![]() and
and ![]() be two real valued function such that
be two real valued function such that ![]() and
and ![]() both exist. Then
both exist. Then
1.
Limit of
sum of two functions ![]() and
and ![]() is the sum of limits of these two functions,
i.e.,
is the sum of limits of these two functions,
i.e.,
![]()
2. Limit of difference of two functions ![]() and
and ![]() is the difference of limits of these two
functions, i.e.
is the difference of limits of these two
functions, i.e.
![]()
3. Limit of product of two
functions ![]() and
and ![]() is the product of limits of these two
functions, i.e.
is the product of limits of these two
functions, i.e.
![]()
4. Limit of quotient of two
functions ![]() and
and ![]() is the quotient of limits of these two
functions (when the denominator is not zero), i.e.,
is the quotient of limits of these two
functions (when the denominator is not zero), i.e.,
Note:
In particular case of
(3), when![]() , where
, where
![]() is real number, then we have
is real number, then we have
![]()
Question. Let![]() . Find the limit of this function at
. Find the limit of this function at![]() .
.
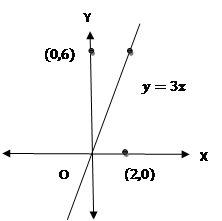 Solution:
Solution:
![]()
![]() .
.
Question.
Consider a function![]() . Find
. Find ![]()
Solution:
![]()
![]()
![]()
![]()
![]()
Question.
Consider a function![]() . Find
. Find![]() .
.
Solution:
![]()
![]()
![]()
Question.
Find![]() , where
, where ![]() is given by,
is given by,
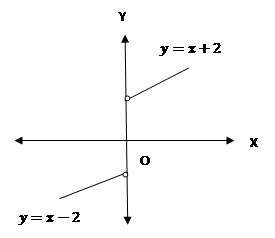
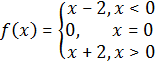
Solution:

![]()
![]()
![]()
And
value of the function ![]() at
at ![]() is
is![]() .
.
Limits
of polynomial and rational functions:
Polynomial function:
If
![]() , where
, where
![]() are real numbers and
are real numbers and ![]() for some
for some ![]() , then
, then ![]() is said to be the polynomial function of
is said to be the polynomial function of ![]() of degree
of degree ![]() .
.
Now ![]() (1)
(1)
So, ![]()
![]()
![]()
![]()
![]() (Using (1))
(Using (1))
Rational function:
A function ![]() is said
to be rational function if
is said
to be rational function if![]() , where
, where
![]() and
and ![]() both are polynomials and
both are polynomials and![]() .
.
And here,

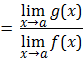
 (1)
(1)
Now if![]() , then
limit of
, then
limit of ![]() at
at ![]() exist.
exist.
And if![]() , then
two cases may arise.
, then
two cases may arise.
Case I:
If![]() , then
the limit does not exist.
, then
the limit does not exist.
Case II:
If
![]()
Let![]() , where
, where
![]() is the
maximum power of
is the
maximum power of ![]() in
in ![]() and
and![]() ,
,
Where![]() is the maximum power of
is the maximum power of ![]() in
in ![]()
If![]() ,
,
then 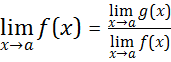
=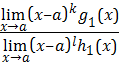
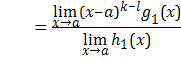
 .
.
If ![]() , then
the limit does not defined.
, then
the limit does not defined.
Theorem: For any
positive integer![]() ,
, ![]()
Proof:
We know that ![]() (1)
(1)
![]() (Using
(1))
(Using
(1))
![]()
![]()
![]()
![]() (
(![]() Times)
Times)
![]()
Question.
Evaluate the following limits.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. 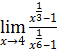 7.
7. ![]() 8.
8. ![]()
Solution:
1.
![]()
![]()
![]()
2. ![]()
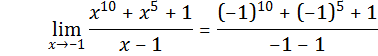
![]()
3. ![]()
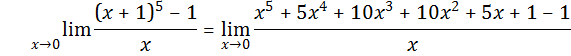
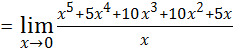
= ![]()
![]()
4.
![]()
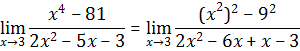
![]()
![]()
![]()
![]()
![]()
5. ![]()
![]()
![]()
![]()
![]()
![]()
6. 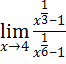
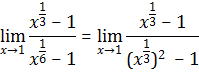
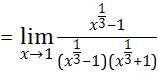


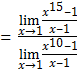 (Using the theorem
(Using the theorem![]() )
)
![]()
![]()
7. ![]()
![]()
![]()
![]()
![]() .
.
Limits of trigonometric functions:
Let us consider two real
functions ![]() and
and ![]() with the same domain such that
with the same domain such that ![]() in the domain of definition
in the domain of definition
and for some ![]()
![]() ,
, ![]() exist. The
exist. The![]() .
.
Sandwich theorem:
Let ![]() be three real functions with the same domain
such that
be three real functions with the same domain
such that ![]() in the domain of definition such that
in the domain of definition such that![]() . If
for some
. If
for some ![]()
![]() and also
and also ![]() then
then![]() .
.
Example:
Evaluate the following
1. ![]() and
2.
and
2. ![]()
Solution:
1. We know that ![]() for
for ![]()
Now ![]() and
and ![]()
So by
sandwich theorem, ![]()
2.
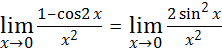
![]()
![]()
![]()
Question.
Evaluate
1. ![]() 2.
2. ![]()
3. 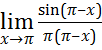 4.
4. ![]()
5. ![]() 6.
6. ![]()
Solution:
1. ![]()
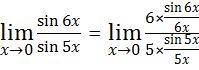
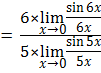
![]()
2. ![]()
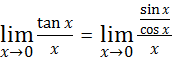
![]()
![]()
![]() .
.
3. 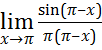
Put
![]() then
then
![]()
![]()
4. ![]()
![]()
![]()
5. ![]()
![]()
![]()
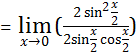

![]()
6. ![]()

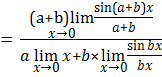 (
(![]() )
)
![]()
Question. Find![]() , where
, where ![]()
Here the
function can be expand as
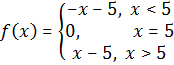
![]()
![]()
And ![]()
![]() .
.
Question.
Let 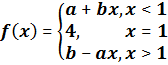 . Find the value of
. Find the value of ![]() and
and ![]() when
when
![]()
![]()
![]()
![]() .
.
Since ![]()
i.e.,
![]() (1)
(1)
And ![]() (2)
(2)
Adding (1) and (2), ![]()
Putting the value of ![]() in (1),
in (1), ![]()
![]() .
.