Dual Nature of Matter
De Broglie’s Equation:
In 1923 doctoral dissertation,
the French physicist Louis de Broglie made a bold assertion. Considering
Einstein's relationship of wavelength, to momentum p, de Broglie proposed that this relationship would determine the
wavelength of any matter, in the relationship:
λ = 
h
= is Planck's constant
p = momentum
This wavelength is called the de
Broglie wavelength. The reason he chose the momentum equation over the energy
equation is that it was unclear, with matter, whether E
should be total energy, kinetic energy, or total relativistic energy. For
photons, they are all the same, but not so for matter.
Problems:
1. What will be the wavelength of a ball of mass
0.1 kg moving with a velocity of 10 m s–1?
Solution:
Mass of the ball m = 0.1 kg
Velocity of the ball 
= 10 m s−1
Momentum of the ball p = mv
= 0.1 × 10
p =
1kg m s−1
Planck’s constant h = 6.626 × 10−34 J s
Wavelength of the ball λ =
= 
=
6.626 × 10−34 m (1J = 1 kg m2s−2)
Wavelength of the ball = 6.626 × 10−34 m or
6.626 × 10−25 nm
2. The mass of an electron is
9.1 × 10–31 kg. If its K.E. is 3.0 × 10–25 J, calculate
its wavelength.
Solution:
Mass of the electron m = 9.1 × 10−31 kg
Kinetic energy of the electron E = 3.0 × 10−25 J
Therefore, velocity of electron
= 
=
=
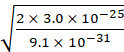
812 m s−1
Wavelength of electron λ =
Planck’s constant h = 6.626 × 10−34 J s
Momentum of the electron p = mv
= 9.1 × 10-31 × 812
=
7389.2 × 10−31
kg m s−1
Wavelength of electron λ = 
= 896.7 × 10-9m
= 896.7 nm
3. Calculate the mass of a photon with wavelength 3.6
Å.
Solution:
Wavelength of the photon = 3.6 Å
= 3.6 × 10−10 m
Velocity of the photon
= Velocity of light
= 3 × 108 m s−1
Planck’s constant h = 6.626 × 10−34 J s
Wavelength λ =
Momentum p = m
m
= h
m = 
= 
=
0.6135 × 10−32 kg
Mass of the photon m = 6.135 × 10−31 kg
4. If the velocity of the
electron in Bohr’s first orbit is 2.19 × 106 m s–1,
calculate the de Broglie wavelength associated with it.
Solution:
According to de Broglie’s
equation,
λ = 
Where,
λ = wavelength associated with the electron
h = Planck’s constant
m = mass of electron
= velocity of electron
Substituting the values in the
expression of λ:
λ = 
= 3.32 × 10−10 m
λ = 332 pm
5. Similar to electron
diffraction, neutron diffraction microscope is also used for the determination
of the structure of molecules. If the wavelength used here is 800 pm, calculate
the characteristic velocity associated with the neutron.
Solution:
From de Broglie’s equation,
λ =
= 
Where,
= Velocity of particle (neutron)
h = Planck’s constant
m = Mass of particle (neutron)
λ = Wavelength
Substituting the values in the
expression of velocity (
),
= 
= 4.94 × 102
m s–1
= 494 m s–1
∴ Velocity associated
with the neutron = 494 m s–1
6. Dual behaviour of matter
proposed by de Broglie led to the discovery of electron microscope often used
for the highly magnified images of biological molecules and other type of
material. If the velocity of the electron in this microscope is 1.6 × 106 m
s–1, calculate de Broglie wavelength associated with this electron.
Solution:
From de Broglie’s equation,
λ =
λ = 
= 4.55 × 10–10 m
λ = 455 pm
∴ de
Broglie’s wavelength associated with the electron is 455 pm.
7. An electron has kinetic
energy 2.8 × 10−23 J. What will be the de Broglie wavelength
of the electron? (Mass of electron is 9.1 × 10−31) ?
Solution:
According to de Broglie
equation,
λ =
= 
= 
= 9.28 × 10−8 m
Hence, de Broglie wavelength
of the electron = 9.28 × 10−8 m.
8. If the velocity of hydrogen
molecule is 5 × 104 cm per sec, then what will be its de
Broglie wavelength?
Solution:
Mass of hydrogen molecule
m = 3.35 × 10−27 kg
Velocity of hydrogen molecule
= 5 × 104 cm/sec
= 500 m/sec
Kinetic energy of the
molecule:
E = 
m
= (3.35 × 10−27 kg)(500 m/sec)2
= 8.375 × 10−25 J
Using the de Broglie equation:
λ =
=
= 
= 9.28 × 10−8 m
9. Calculate the de Broglie
wavelength of CO2 moving with a velocity of 440 m/s.
Solution:
From de Broglie’s equation,
λ =
Where,
λ = wavelength
m = Mass of CO2 molecule
Mass of 1 mole (6.02 × 1023 molecules)
of CO2 ,
= 44
g
Thus mass of 1 molecule of CO2 would
be (in Kg),
= 
= Velocity of CO2
λ = 
λ = 2.061 × 10−11 m
λ = 20.61 × 10−12 m
λ = 20.61 pm
Heisenberg Uncertainty Principle:
The Heisenberg uncertainty principle states that
there is a fundamental limit to how well you can simultaneously know the
position and momentum of a particle. This means if you know the position
very precisely, you can only have limited information about its momentum and
vice-versa.
Let's do a small experiment. Place a cam and record
the entire experiment.
Take a chalk piece and throw it above your head and
try to catch. Now, stop your recording and view it. While viewing, you can
either pause the particular frame where the chalk piece attains the position
that you wanted to see it in or you can see the train of frames to see the time
and calculate the momentum of that chalk. It becomes impossible to freeze an
object at a particular position and calculate the momentum at that position.
Likewise, the Heisenberg principle. "It is impossible to calculate both
the position and momentum of a particle with accuracy".
Mathematically, it can be given as in equation:
Δ
× Δ
≥ 
or Δ
× Δm
≥
or Δ
× Δ ≥ 
Where,
Δ is the uncertainty in position,
Δ (or Δ) is the uncertainty in momentum
(or velocity) of the particle.
If the position of the electron is known with high degree of accuracy
(Δ is small), then the velocity of the electron
will be uncertain (Δ is large).
On the other hand, if the velocity of the electron is known precisely
(Δ is small), then the position of the electron
will be uncertain (Δ will be large).
Thus, if we carry out
some physical measurements on the electron’s position or velocity, the outcome
will always depict a fuzzy or blurry picture.
Problems:
1. A
microscope using suitable photons is employed to locate an electron in an atom
within a distance of 0.1 Å. What is the uncertainty involved in the measurement
of its velocity?
Solution:
Position
of the photon
0.1 Å
0.1 × 10−10m
We
assume, mass of the photon m = 9.11 × 10−31kg
Planck’s constant h = 6.626 × 10−34 J s
Δ · Δ =
Δ = 
=
=
0.579 × 107
m s−1
=
5.79 × 106
m s−1
2. A
golf ball has a mass of 40 g, and a speed of 45 m s−1. If the
speed can be measured within accuracy of 2%, calculate the uncertainty in the
position.
Solution:
Mass of
the golf ball m = 40 g
= 40 × 10−3 kg
Speed of
the golf ball
= 45 m s−1
= 45 × 
= 0.9 m s−1
Uncertainty
of the position Δ · Δ =
Δ =
= 
= 1.465 × 10−33 m
|
|
|
|
