Exercises
1. Physical behaviour of the states differs
greatly even though chemical behaviour of the three states is identical
because:
a.
Chemical properties depend on
intermolecular non-bonding forces whereas physical properties depend on
intermolecular bonding forces
b.
Chemical properties depend on
non-bonding forces whereas physical properties depend on intermolecular bonding
forces
c.
Chemical properties depend on
intramolecular bonding forces whereas physical properties depend on
intermolecular bonding forces
d.
Chemical properties depend on
covalent bonding forces whereas physical properties depend on energy supplied
Solution: Chemical properties depend on
intramolecular bonding forces whereas physical properties depend on
intermolecular bonding forces.
Physical properties of an element
depends on the intermolecular forces of that element which in turn changes on
variations in temperature, pressure and volume, whereas, chemical properties
depend upon intramolecular forces which remain the same for that element until
another element is introduced.
2. Dipole-dipole forces act between molecules
that have:
a.
An induced electrical dipole moment
b.
A permanent electrical dipole moment
c.
An electron cloud that causes
temporary dipoles
d.
A permanent magnetic dipole moment
Solution: A permanent electrical dipole moment
Dipole moments depend upon the
electron charge of the molecules.
3. Which of the following statements about
Hydrogen bond incorrect?
a.
In hydrogen bonding H atom becomes
partially positive and is attracted to the more negative O atom
b.
In hydrogen bonding H atom becomes
partially positive and is attracted to the more negative F atom
c.
In hydrogen bonding H atom becomes
partially negative and is attracted to the more positive N atom
d.
In hydrogen bonding H atom becomes
partially positive and is attracted to the more negative N atom
Solution: In hydrogen bonding H atom becomes
partially negative and is attracted to the more positive N atom
In hydrogen bonding the H atom
becomes partially positive in order to create a hydrogen bond.
4. The intermolecular force primarily
responsible for the condensed states of nonpolar substances is the:
a.
Dispersion force (or London force)
b.
Dipole – dipole force
c.
Hydrogen bond
d.
Ion-dipole forces
Solution: Dispersion force (or London force)
London or dispersion forces create
temporary dipole moment for nonpolar molecules to form intermolecular bonds.
5. The average Kinetic energy and Thermal
energy are proportional to the:
a.
Pressure
b.
Volume
c.
Specific heat
d.
Absolute temperature
Solution: Absolute temperature
As
increase or decrease in temperature leads to change in kinetic and thermal
energy hence it is directly proportional.
6. Three states of matter are the result of:
a.
Balance between intermolecular forces
and the thermal energy of the molecules
b.
Balance between Van der Waals forces
and the London forces
c.
Balance between intermolecular forces
and the intramolecular bonding energy of the molecules
d.
Balance between Hydrogen bonding
forces and the London forces
Solution: Balance between intermolecular
forces and the thermal energy of the molecules
The intermolecular forces between
the molecules of matter change due to application of thermal energy from solid
to liquid, and liquid to gas.
7. Gases have much lower density than the
solids and liquids because:
a.
Gases contain lower specific enthalpy
than solids
b.
Thermal energy overcomes the the attractive intermolecular forces
c.
Distance between the molecules is
small compared to solids
d.
Gases do not have intermolecular
forces that attract each molecule to another
Solution: Thermal energy overcomes the the attractive intermolecular forces
As thermal energy is applied to a
gas it pushes the molecules further apart and reduces the intermolecular force
between them, thus decreasing the density of the gas.
8. Increase in kinetic energy can overcome
intermolecular forces of attraction. How will the viscosity of liquid be
affected by the increase in temperature?
a.
Decrease
b.
No regular pattern will be followed
c.
No effect
d.
Increase
Solution: Decrease
Intermolecular force of liquid
decreases with increase in temperature, hence viscosity of liquid also
decreases. However, some exceptions are there like liquid proteins and liquid
sulphur.
9. Behaviour of the gas becomes more ideal
when:
a.
Pressure is very low
b.
Pressure is very high
c.
Number of moles is very low
d.
Temperature is very low
Solution: Pressure is very low
The
real gases show ideal behaviour when pressure approaches zero.
10. Critical temperature (TC) of carbon dioxide is the highest temperature at
which liquid carbon dioxide is observed. Above this temperature:
a.
It is gas
b.
It is liquid
c.
It is mixture of solid and liquid
d.
It is solid
Solution: It is gas
Liquid carbon dioxide first appears at 31 ͦ C, which
is called critical temperature Tc.
Above TC carbon dioxide is a gas and below it, it is a liquid.
11. Above the critical
temperature (TC) of carbon
dioxide:
a.
Solidification of the gas is possible
b.
Liquefaction of the gas is possible
c.
Increase of pressure makes
d.
Liquefaction of the gas is not
possible
Solution: Liquefaction of the gas is not
possible
Critical temperature of a gas is
highest temperature at which liquefaction of the gas first occurs and for
further liquefaction the gas has to be cooled.
12. The three states of matter of H2O
are in equilibrium at:
a.
Steam point
b.
Ice point
c.
Critical point
d.
Triple point
Solution: Triple point
Triple point is the point on a
phase diagram at which the three states of matter: gas, liquid, and solid
coexist or are in equilibrium.
13. Surface tension decreases as the
temperature is raised because:
a.
Increase in temperature increases the
kinetic energy of the molecules and effectiveness of intermolecular attraction
increases
b.
Increase in temperature decreases the
kinetic energy of the molecules and effectiveness of intermolecular attraction
decreases
c.
Increase in temperature decreases the
kinetic energy of the molecules and effectiveness of intermolecular attraction
is not changed
d.
Increase in temperature increases the
kinetic energy of the molecules and effectiveness of intermolecular attraction
decreases
Solution: Increase in temperature increases
the kinetic energy of the molecules and effectiveness of intermolecular
attraction decreases
The magnitude of surface tension of
a liquid depends on the attractive forces between the molecules. When the
attractive forces are large, the surface tension is large. Increase in
temperature increases the kinetic energy of the molecules and effectiveness of
intermolecular attraction decreases, so surface tension decreases as the
temperature is raised.
14. Water has high surface tension and high
capillarity because of:
a.
Ionic bonds
b.
Hydrogen bonds
c.
Dispersion forces
d.
Covalent bonds
Solution: Hydrogen bonds
Hydrogen
bonds are very strong. As the attractive forces are large, the surface tension
and capillarity of water is high.
15. What will be the minimum pressure required
to compress 500 dm3 of air at 1 bar to 200 dm3 at 30 ͦ
C?
Solution:
We have,
p1 = 1 bar
p2 = ?
V1 = 500 dm3
V2 = 200 dm3
T = is constant at 30 ͦC
According to Boyle’s law,
![]() =
=
![]()
p2 = ![]()
= 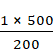
= 2.5 bars
16. A vessel of 120 mL capacity contains a
certain amount of gas at 35 ͦ C and 1.2 bar pressure. The gas is
transferred to another vessel of volume 180 mL at 35 ͦ C. What would be
its pressure?
Solution:
We have,
p1 =
1.2 bar
p2 = ?
V1 =
120 mL
V2 =
180 mL
T = is constant at 35 ͦC
According to Boyle’s law,
![]() =
=
![]()
p2
=
![]()
= 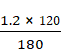
= 0.8 bars
17. At 0 ͦ C the density of a certain
oxide of a gas at 2 bar is same as that of di-nitrogen at 5 bar. What is the
molecular mass of the oxide?
Solution:
We have,
p1 = 2 bar
p2 = 5 bar
M = Relative atomic mass × Molar mass constant (1
g/mol)
Molar mass of dinitrogen
M1 = 2 × 14 × 1
= 28 g/mol
We know that
d = ![]()
For dinitrogen,
d1 = ![]()
For unknown oxide,
d2 = ![]()
Since
d1 = d2
![]() =
= ![]()
140 = 2 × M
M = ![]()
= 70 g/mol
18. Pressure of 1 g of an ideal gas A at 27 ͦ
C is found to be 2 bar. When 2 g of another ideal gas B is introduced in the
same flask at same temperature the pressure becomes 3 bar. Relationship between
their molecular masses is:
Solution:
We have,
pA = 2 bar
pTotal = 3 bar
pB = 3 – 2
= 1 bar
mA = 1 g
mB = 2 g
Substituting in equation,
pV = nRT
pV = ![]() RT
RT
p = ![]()
p = ![]()
2 = ![]() ------
(1)
------
(1)
1 = ![]() ------
(2)
------
(2)
Equating (1) and (2),
![]() =
= ![]()
![]() =
= 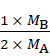
Therefore we get,
MB = 4MA
19. The drain cleaner, drainex
contains small bits of aluminium which react with caustic soda to produce
dihydrogen. What volume of dihydrogen at 20 ͦC and one bar will be released
when 0.15 g of aluminium reacts?
Solution:
Aluminium
in drainex reacts with caustic soda to produce
dihydrogen.
2Al
+ 2NaOH + 2H2O → 2NaAlO2 + 3H2
2
moles of aluminium → 3 moles of dihydrogen
⇒
2 × 27 g = 54 g ⇒ 3 × 22.40 L
Therefore,
= 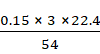
= 0.1867 L
= 187 ml
We have,
p1 = 1 bar
p2 = 1 bar
T1 = 273 K
T2 = 20 + 273
= 293 K
V1 = 187 ml
V2 = ? ml
We
know that,
V2 = ![]()
= 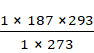
= 200.699 ml
= 201 ml approximately 202.5 ml
20. What will be the pressure exerted by a
mixture of 3.2 g of methane and 4.4 g of carbon dioxide contained in a 9 dm3
flask at 27 ͦ C?
Solution:
We know that,
Mass of carbon dioxide m1 = 4.4 g
Molar mass of carbon dioxide M1 = 44 g/mol
Mass of methane m2 = 3.2 g
Molar mass of methane M2 = 16 g/mol
Now,
Amount of carbon dioxide n1 = ![]()
= 0.1 mole
Amount of methane n2 = ![]()
= 0.2 mole
Therefore total moles n = n1 + n2
= 0.1 + 0.2
= 0.3 mole
Ideal
gas equation is,
pV
= nRT
We
know that,
R = 0.083 bar dm3 K−1
mol−1
T =
27 ͦC
= 27 + 273
= 300 K
V =
9 dm3
p = ![]()
= 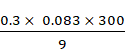
= 0.83 bar
= 0.83 × 105
Pa (1 bar = 105 Pa)
= 8.3 × 104
Pa
The pressure exerted by both gases
is 8.3 × 104 Pa.
21. What will be the pressure of the gaseous
mixture when 0.5 L of H2 at 0.8 bar and 2.0 L of O2 at
0.7 bar are introduced in a 1 L vessel at 27 ͦ C?
Solution:
We have,
V1 = 0.5 L
V2 = 2.0 L
p1 = 0.8 bar
p2 = 0.7 bar
We know that,
pV = nRT
So for H2,
0.8 × 0.5 = n1RT
n1 = ![]()
So for O2,
0.7 × 2.0 = n2RT
n2 = ![]()
Using Dalton’s law of partial pressures,
When the mixture is put in a 1 L vessel,
p × 1
L = (n1 + n2)
× RT
p = 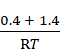 × RT
× RT
p = 1.8 bars
The pressure of the mixture of gases
is 1.8 bars.
22. Density of a gas is found to be 5.46 g/dm3
at 27 ͦ C at 2 bar pressure. What will be its density at STP?
Solution:
We have,
d1 = 5.46 g/dm3
T1 = 27 ͦC
= 27 + 273 K
= 300 K
= 2 bars
At standard temperature and
pressure,
d2 = ?
T2 = 0 ͦC
= 273 K
p2 = 1 bar
Using Molar mass formula from ideal
gas equation,
M = ![]()
Therefore,
![]() =
= ![]()
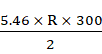 =
= 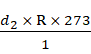
d2 = 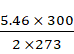
= 3 g/mol
At standard temperature and pressure
density is 3 g/mol.
23. 34.05 mL of phosphorus vapour weighs 0.0625
g at 546 ͦ C and 0.1 bar pressure. What is the molar mass of phosphorus
Solution:
We
have,
V = 34.05 mL
= 0.03405 L
T = 546 ͦC
= 546 + 273 K
= 819 K
p = 0.1 bars
m = 0.0625 g
R =
0.0821 L atm K-1 mol
-1
From
ideal gas equation we can find molar mass,
M = ![]()
=
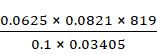
= 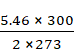
= 1234.212 mol-1
The
molar mass of Phosphorous is 1234.212 mol-1.
24. Calculate the temperature of 4.0 mol of a gas occupying 5 dm3 at 3.32 bar. (R = 0.083 bar dm3 K−1mol−1).
Solution:
We
have,
V = 5 dm3
p
= 3.32 bar
R
= 0.083 bar dm3 K−1
mol−1
n = 4 mol
Using
ideal gas equation,
pV = nRT
T = ![]()
= 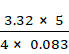
= 50 K
The
temperature of the gas is 50 K.
25. Calculate the total number of electrons
present in 1.4 g of dinitrogen gas.
Solution:
We
know that,
Mass
of N2 m = 1.4 g
Molar
mass of N2 M = 28 g/mol
Moles
of N2 n = ![]()
= 0.05 mol
The
number of nitrogen molecules in 0.05 mol of N2,
= 0.05 × 6.023 × 1023
= 0.30115 × 1023
= 3.0115 × 1022
Number
of electrons in 1 molecule of N2 = 14 electrons
Therefore,
= 3.0115 × 1022 × 14
= 4.22 × 1023 electrons
The number
of electrons in 1.4 g of dinitrogen is 4.22 × 1023.
26. The Van der Waals Equation adjusts the
measured volume:
a.
Up by subtracting a factor from the
entire container volume that accounts for the molecular volume
b.
Down by adding a factor from the
entire container volume that accounts for the molecular volume
c.
Down by subtracting a factor from the
entire container volume that accounts for the molecular volume
d.
Up by subtracting a factor from the
entire container volume that accounts for the container volume
Solution: Down by subtracting a factor from the entire container volume that
accounts for the molecular volume
Van
der Waals proposed that we correct the volume of
a real gas as it is too large at high pressures by subtracting a term from the volume of the real gas before
we substitute it into the ideal gas equation. He therefore introduced a
constant constant (b) into the
ideal gas equation that was equal to the volume actually occupied by a mole of
gas particles.
27. The Van der Waals Equation adjusts the measured
pressure:
a.
Up by adding a factor that accounts
for intermolecular attractions
b.
Up by subtracting a factor that
accounts for intermolecular attractions
c.
Down by adding a factor that accounts
for intermolecular attractions
d.
Up by adding a factor that accounts
for intramolecular attractions
Solution: Up by adding a factor that accounts
for intermolecular attractions
Van
der Waals added a term to the pressure as it was too small. This term
contained a second constant (a) and has the form: ![]() .
.
28. Pay load is defined as the difference
between the mass of displaced air and the mass of the balloon. Calculate the
pay load when a balloon of radius 10 m, mass 100 kg is filled with helium at
1.66 bar at 27 ͦC. (Density of air = 1.2 kg m−3 and R = 0.083 bar dm3 K−1
mol−1).
Solution:
Payload
= mass of
displaced air − mass of balloon
We
have,
Radius
of balloon = 10 m
Mass
of balloon = 100 kg
Volume
of balloon/sphere
= ![]()
= 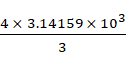
= 4188.79 m3
Density of air = 1.2 kg m-3
Mass
of air displaced by the balloon,
= 1.2 ⨯ 4188.79
= 5026.548 kg
Ideal
gas equation is,
pV = nRT
We
know that,
R = 0.083 bar dm3 K−1
mol−1
T = 27 ͦC
= 27 + 273
= 300 K
Molar
mass of Helium = 4 g/mol
N = ![]()
pV = ![]() RT
RT
m = ![]()
m = 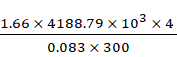
= 1117.010 kg
Total
mass of balloon = 1117.010 + 100
= 1217.010 kg
Payload
of balloon = mass of displaced air – mass of
balloon
= 5026.548 – 1217.010
= 3809.538 kg
The payload of the balloon is
3809.538 kg.
29. Calculate the volume occupied by 8.8 g of
CO2 at 31.1 ͦ C and 1 bar pressure. R = 0.083 bar dm3 K−1
mol−1.
Solution:
We
have,
Mass
of CO2 , m = 8.8 g
T = 31.1 ͦ C
= 31.1 + 273
= 304.1 K
p = 1 bar
R
= 0.083 bar dm3 K−1
mol−1
Molar
mass of CO2, M = 44 g/mol
Using
ideal gas equation,
pV = nRT
n = ![]()
Therefore,
pV = ![]() RT
RT
V = ![]()
= 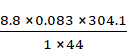
= 5.04806 L
The volume of CO2 is
5.04806 L.
30. 2.9 g of a gas at 95 ͦ C occupied the
same volume as 0.184 g of dihydrogen at 17 ͦ C, at the same pressure. What
is the molar mass of the gas?
Solution:
We
have,
For
gas 1,
m1 = 2.9 g
T1 = 95 ͦ C
= 95 + 273
= 368 K
m2 = 0.184 g
T2 = 17 ͦ C
= 17 + 273
= 290 K
p1 = p2
V1 = V2
R = 0.083 bar dm3 K−1 mol−1
Molar
mass of Dihydrogen,
M2 = 2.01588 g/mol
Using
ideal gas equation,
p1V1 = n1RT1
p2V2 = n2RT2
n2 = ![]()
= 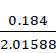
= 0.0913 moles
V2 = ![]()
= 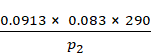
V2 = ![]() L
L
Since
p1 = p2
and V1 = V2
V1 = ![]() L
L
We
can find n1 by
substituting V1
p1V1 = n1RT1
p1 × ![]() = n1
× 0.083 × 368
= n1
× 0.083 × 368
n1 = 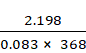
n1 = 0.072 moles
![]() =
= ![]()
M1 = ![]()
= ![]()
= 40.3 g/mol
The payload of the balloon is 40.3
g/mol.
31. A mixture of dihydrogen and dioxygen at one
bar pressure contains 20 % by weight of dihydrogen. Calculate the partial
pressure of dihydrogen.
Solution:
We know from Dalton’s law of partial pressures,
pi = ![]() × pTotal
× pTotal
where,
![]() =
= ![]()
Assume
total mass is 100 g,
Mass
of dihydrogen m1 = 20 % of 100g
= 20 g
Molar
mass of dihydrogen M1 = 2 g/mol
Number
of moles of dihydrogen n1 = ![]()
= ![]()
= 10 moles
Mass
of dioxygen m2 = 100 – 20
= 80 g
Molar
mass of dioxygen M2 = 32 g/mol
Number
of moles of dioxygen n2 = ![]()
= ![]()
= 2.5 moles
Total pressure of both
gases ptotal = 1 bar
Total number of moles n
= 10 + 2.5
= 12.5 moles
Mole fraction of
dihydrogen x1
= ![]()
= ![]()
= 0.8
Partial pressure of
dihydrogen p1 = ![]() × ptotal
× ptotal
= 0.8 × 1
= 0.8 bar
The partial pressure of dihydrogen in
the mixture is 0.8 bar.
32. The vapour pressure of different substances
at the same temperature increases if:
a.
The molecules of the substance are
covalent bonded
b.
The intermolecular forces of the
substance are weak
c.
The intermolecular forces of the
substance are strong
d.
The molecules of the substance are
ionic bonded
Solution: The intermolecular forces of the
substance are weak
As temperature increases,
intermolecular forces become weak. Different substances have different boiling
points and the vapour pressure increases as temperature increases.
33. A person living in ooty
observed that cooking food without using pressure cooker takes more time. The
reason for this observation is that at high altitude:
a.
Pressure increases
b.
Temperature increases
c.
Pressure decreases
d.
Temperature decreases
Solution: Pressure decreases
When a liquid is heated, it will
turn into vapour at a certain temperature.
In an open container, these molecules will wander off (diffuse) into the room
and out into the atmosphere. Eventually all the liquid will evaporate. Pressure
decreases and no cooking takes place. But in a pressure cooker there will be
repeated evaporation and condensation leading to pressure being maintained till
a certain point. Hence cooking is easier in a pressure cooker.
34. Which of the following property of water
can be used to explain the spherical shape of rain drops?
a.
Surface tension
b.
Critical phenomena
c.
Pressure
d.
Viscosity
Solution: Surface tension
Liquid drops will be spherical as a spherical shape has
the minimum surface energy for a given volume.
35. The interaction energy of London force is
inversely proportional to sixth power of the distance between two interacting
particles but their magnitude depends upon:
a.
Charge of interacting particles
b.
Polarisability of interacting particles
c.
Mass of interacting particles
d.
Strength of permanent dipoles in the particles
Solution: Polarisability of interacting particles
Large electron clouds get easily
polarised. Increase in polarisation leads to an increase in the magnitude of
the London force.
36. The pressure of a 1 :
4 mixture of dihydrogen and dioxygen enclosed in a vessel is one atmosphere.
What would be the partial pressure of dioxygen?
Solution:
Let the number of moles of
dihydrogen and dioxygen be 1 and 4.
Mole fraction of O2 = 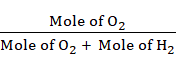
= ![]()
= ![]()
= 0.8
Partial pressure of dioxygen
= Mole fraction × Total Pressure
= 0.8 × 1
= 0.8 atm
= 0.8 × 105 Nm−2
= 8 × 104 Nm−2
The partial pressure of dioxygen is
8 × 104 Nm−2.
37. Increase in kinetic energy can overcome
intermolecular forces of attraction. How will the viscosity of liquid be
affected by the increase in temperature?
a.
No regular pattern will be followed
b.
Increase
c.
No effect
d.
Decrease
Solution: Decrease
Viscosity of liquids decreases as
the temperature rises because at high temperature molecules have high kinetic
energy and can overcome the intermolecular forces to slip past one another
between the layers.
38. With regard to the gaseous state of matter
which of the following statements is correct?
a.
Complete order of molecules and fixed
position of molecules
b.
Complete disorder of molecules and
Random motion of molecules
c.
Fixed position of molecules and
complete order of molecules
d.
Random motion of molecules and fixed
position of molecules
Solution: Complete disorder of molecules and
Random motion of molecules
In gaseous state, molecules are in a
state of random motion, i.e., it is the state in which molecules are disorderly
arranged. Gaseous state has higher entropy than the liquid as well as solid.
39. Under which of the
following two conditions, a gas deviates most from the ideal behaviour?
a.
High temperature and Low pressure
b.
High pressure and Low temperature
c.
Low temperature only
d.
Low pressure only
Solution: High temperature and Low pressure
Real gases show ideal behaviour when
temperature is high and pressure is low and the intermolecular forces are
practically negligible. Thus to deviate from ideal behaviour temperature has to
below and pressure high.
40. Heat of vaporization is always larger than
the heat of fusion because:
a.
It takes more energy to separate
particles completely than just to free them from their fixed positions in the
solid
b.
It takes less energy to separate particles
completely than just to free them from their fixed positions in the solid
c.
It takes more energy to separate
particles completely than just to free them from their random positions in the
solid
d.
It takes no energy to separate
particles completely than just to free them from their oscillating positions in
the solid
Solution: It takes more energy to separate
particles completely than just to free them from their fixed positions in the
solid
The energy required to completely separate the
molecules, moving from liquid to gas, is much greater that if you were just to reduce their separation,
solid to liquid.
41. The ease with which the electron cloud of a
particle can be distorted is called its:
Solution: Polarizability
Neutral nonpolar species have spherically symmetric
arrangements of electrons in their electron clouds. When in the presence of an
electric field, their electron clouds can be distorted. The ease of this
distortion is defined as the polarizability of the atom or molecule.
42. Capillarity results from a competition
between the:
a.
Intramolecular forces within the
liquid (cohesive forces) and those between the liquid and the tube walls
(adhesive forces)
b.
Intermolecular forces within tubewall and intramolecular forces within tubewall
c.
Intermolecular forces within the
liquid (cohesive forces) and those between the liquid and the tube walls
(adhesive forces)
d.
Intermolecular forces within liquid
and intramolecular forces within liquid
Solution: Intermolecular
forces within the liquid (cohesive forces) and those between the liquid and the
tube walls (adhesive forces)
The rise of water in a thin tube inserted in water is
caused by forces of attraction between the molecules of water (intermolecular
forces) and the glass walls and among the molecules of water themselves.
43. Acetylene (C2H2), an
important fuel in welding, is produced in the laboratory when calcium carbide
(CaC2) reacts with water:
CaC2 (s) + 2H2O
(l) → C2H2 (g) + Ca(OH)2
(aq)
For a sample of acetylene collected over water,
total gas pressure (adjusted to barometric pressure) is 738 torr
and the volume is 523 mL. At the temperature of the
gas (23 ͦ C), the vapour pressure of water is 21 torr.
How many grams of acetylene are collected?
Solution:
We
have,
P = Total gas pressure 738 torr − Vapor pressure of
the water 21 torr
= 717 torr
of C2H2
T = 23 C + 273
= 296 K
V = 523 ml
= 0.523 L
As
per Ideal Gas equation
pV = nRT
717 × 0.523 = n ×
62.36 × 296 K
n = 0.02032 moles of C2H2
Molar
mass of C2H2 M = 26.04 g/mol
Moles
of C2H2 m = n
× M
= 0.02032 × 26.04
Mass
of N2 m = 0.529 g of C2H2
There are 0.529 g of C2H2.
44. A scale model of a blimp rises when it is filled
with helium to a volume of 55.0 dm3. When 1.10 mol
of He is added to the blimp, the volume is 26.2 dm3. How many more
grams of He must be added to make it rise? Assume constant T and P.
Solution:
We
have,
Initial
readings of blimp,
n = 1.10 mol
V = 26.2 dm3
p = T
= k
R
= 0.083 bar dm3 K−1
mol−1
Using
ideal gas equation,
pV = nRT
![]() =
= ![]()
= 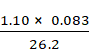
= 0.0035 atm/K
Final
readings of blimp,
n = ? mol
V = 55.0 – 26.2
= 28.8 dm3
p = T
= k
R
= 0.083 bar dm3 K−1
mol−1
Using
ideal gas equation,
pV = nRT
n = ![]() × k
× k
= ![]() × 0.0035
× 0.0035
= 1.214 mol
Mass
of Helium
m = 1.214 × 4 (Molar mass of He = 4 g/mol)
= 4.856 g
The mass of Helium needed to fill up the blimp
is 4.856 g.
45. What mass of potassium chloride forms when
5.25 L of chlorine gas at 0.950 atm and 293 K reacts
with 17.0 g of potassium?
Solution:
The reaction is,
2K + Cl2 → 2KCl
We
know that,
T = 293 K
V = 5.25 L
p
= 0.950 atm
m = 17.0 g
R
= 0.083 bar dm3 K−1
mol−1
Using
ideal gas equation,
pV = nRT
n = ![]()
= 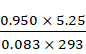
= 0.205 mol
Mass
of Potassium chloride,
m = 0.205 × 74.55 (Molar mass of KCl = 74.55 g/mol)
= 15.28275 g
Since
there are 2 moles,
m = 2 × 15.28275
= 30.5655 g
The mass of KCl
formed is 30.5655 g.
46. Which of the following is correct for
critical temperature?
a. At critical temperature the gas and
the liquid phases have different critical densities
b. It is the lowest temperature at
which liquid and vapour can coexist
c. Beyond the critical temperature,
there is no distinction between the two phases and a gas cannot be liquefied by
compression
d. At critical temperature (Tc), the surface tension of
the system is not zero
Solution: Beyond the critical temperature,
there is no distinction between the two phases and a gas cannot be liquefied by
compression
Critical temperature of a substance
is a temperature at and above which gases can't be liquid fied,
no matter how much pressure is applied.
47. If a gas is heated at constant pressure,
its density
a. Will decrease
b. Will increase
c. May increase or decrease
d. Will remain unchanged
Solution:
Will decrease
When gas is heated at constant
pressure the molecules gain energy and thus disperseand
amount of gas at a particular place decreases so density decreases.
48. One gram mole of a gas at NTP occupies 22.4
L as volume. This fact was derived from:
a. Dalton's theory
b. Avogadro's hypothesis
c. Berzelius hypothesis
d. Law of gaseous volumes
Solution:
Will decrease
Avagadro gave a hypothesis stating that the
volume of gas is directly proportional to the number of molecules of gas. As one
moles of substance always contains same number of molecules i.e., 6.022 × 1023.
So the volume is always 22.4 h at NTP. NTP is normal temperature.