First Law of
Thermodynamics
Definition
The First Law of Thermodynamics
states that heat is a form of energy, and thermodynamic processes are therefore
subject to the principle of conservation of energy. This means that heat energy
cannot be created or destroyed. It can, however, be transferred from one
location to another and converted to and from other forms of energy.
ΔQ = ΔU + W
where
ΔQ is the heat supplied to the
system by the surroundings
ΔU is the change in internal
energy of the system
ΔW is the work done by the
system on the surroundings
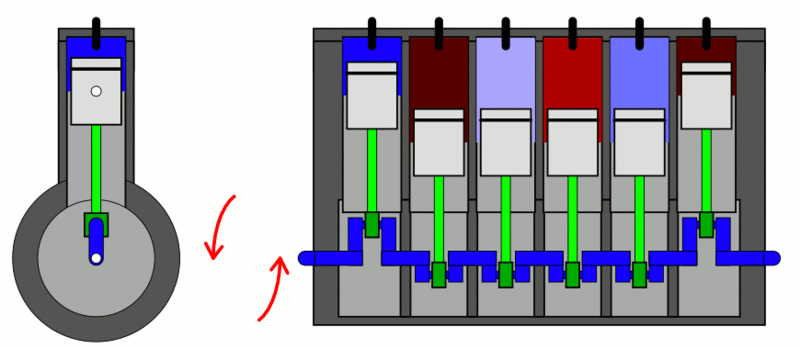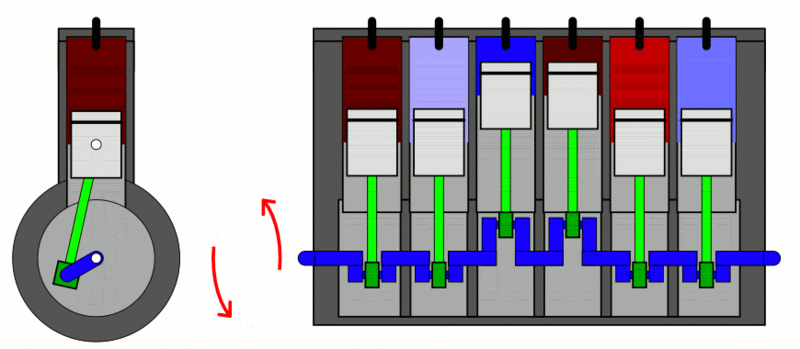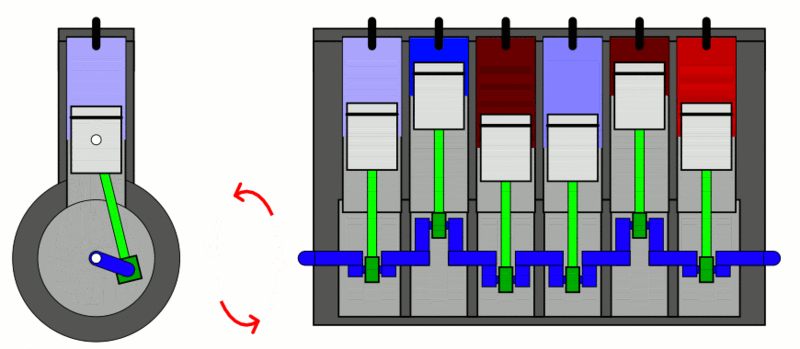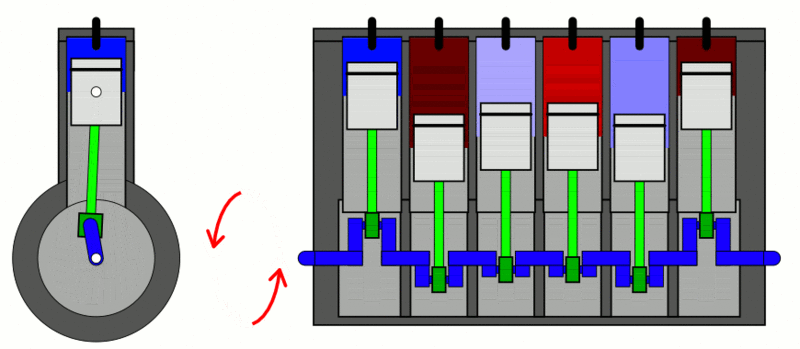
Examples
of the first law of thermodynamics: Internal Combustion Engine
Sign convention
·
When work is done by the
system, ΔW is positive.
·
When work is done on the
system, ΔW is negative.
·
When heat is given to the
system, ΔQ is positive.
·
When heat is given by the
system, ΔQ is negative.
Differential form of First law of Thermodynamics
δU
= δQ − δW
where
W is the work done
U is the internal energy of the system
Q is the heat supplied
Qualitative Explanation of First Law of Thermodynamics
The internal
energy δU of a system can change
through two modes of energy transfer: heat and work. Let
δQ
= Heat supplied to the system by the surroundings
δW = Work done by the system on the
surroundings
δU = Change in the internal energy of the
system
The general principle
of conservation of energy implies that
ΔQ = ΔU+δW
i.e., the energy (δQ) supplied to the system goes in partly to increase
the internal energy of the system (δ U) and the rest in work on the
environment (δW). This
is known as the First Law of Thermodynamics. It is simply the general law of
conservation of energy applied to any system in which the energy transfer from
or to the surroundings is taken into account.
Some Important
results
1.
For isothermal irreversible
expansion q=-w =Pext (V2-V1)
2.
For isothermal reversible
expansion or compression from volume V1 to V2 or pressure P1 to P2 ,
q –w =nRT ln
=nRT ln 
3.
For isothermal expansion of an ideal gas
against vaccum, (i.e., for free expansion)
∆U=0, 
=0, 
=0.
4.
Since internal energy (U) of an ideal gas
is a function of temperature ,for all isothermal processes, involving ideal gas
, ∆U=0, whether the process is reversible or
irreversible .
5.
For adiabatic change,
=0, therefore , ∆U=wad .
Problems
1. A
gas expands from a volume of 1 m3 to a volume
of 2 m3 against an
external pressure of 105 N m-2. The work done by the gas
will be
(a) 105
kJ
(b) 102
kJ
(c) 102
J
(d) 103
J
Solution:
q = -w = Pext (V2-V1)
from
the data given in the question ,
V2 =
2 m3
; V1 = 1 m3; Pext = 105 N m-2.
= -P∆V = -105 N m-2(2-1)
m3 = -105 N m
=-105J = -102kJ
2. Calculate the work done (in joules) when 0.2 mole
of an ideal gas at 300 K expands isothermally and reversibly from initial
volume of 2.5 litres to the final volume of 25 litres
(a) 996
(b) 1148
(c) 11.48
(d) 114.8
Solution:
q –w = nRT ln
from
the data given in the question ,
V2 =
25 m3
; V1= 2.5 m3; n =
0.2; R = 8.314; T = 300K.
w =
-2.303 
n
R
log 
w =
-2.303 0.28.314
log 
=
-1148
4. Calculate the work done when 1 mole of an ideal
gas is compressed reversibly from
1.0 bar to 4.00 bar at constant temperature of 300 K
(a) 3.46 kJ
(b) - 8.20 kJ
(c) 18-02 kJ
(d) - 14-01 kJ
Solution:
q –w = nRT ln
from
the data given in the question ,
P2 =
4 bar
; P1 = 1 bar; n = 1; R = 8.314; T = 300K.
w =
-2.303 n
R log 
w =
-2.303 1 8.314 
log 
=
3.458 kJ
5. A piston filled with 0.04 mol
of an ideal gas expands reversibly from 50.0 mL to 375 mL at a constant
temperature of 37.0°C.As it does so, it absorbs 208 J of heat. The
values of q and w for the process will be: (R = 8.314 J/mol
K, In 7.5 = 2:01)
(a) q = + 208 J, W = + 208 J
(b) q = + 208 J, w = - 208 J
(c) q = - 208 J, w = - 208 J
(d) q = - 208 J, w = + 208 J
Solution:
For isothermal expansion of an ideal gas,
∆U = 0.
Hence, from first law of thermodynamics, ∆U = q + w, we have q = -w.
As process
involves adsorption of heat, i.e., it is endothermic, q = +208J
∴ w = -208J
6.
Which of the following is correct option for free expansion of an ideal gas
under adiabatic condition?
(a) q = 0, ∆T
< 0, w ≠ 0
(b) q = 0, ∆T ≠ 0 w=0
(c) q ≠ 0, ∆T
= 0, w = 0
(d) q = 0, ∆T = 0, w=0
Solution:
For adiabatic change,
= 0
For free expansion Pext
= 0.
Hence, w = 0
∆U = q+w =
0+0 = 0.
As U is a function of temperature (U = 
nRT)
and as ∆U = 0, ∴ ∆T = 0
7.
When 1 mol of a gas is heated at constant volume,
temperature is raised from 298 to 308 K. Heat supplied to the gas is 500 J.
Then which statement is correct?
(a) q = W = 500 J, ∆U = 0
(b) q = ∆U = 500 J, W = 0
(c) q = W = 500 J, ∆U = W = 0
(d) ∆U = 0, q = W = - 500 J
Solution:
At constant volume,
∆V = 0.
Hence W=0.
Further
∆ U = q +W.
As W = 0, ∆ U = q = 500J
8. Based on first law of thermodynamics, which one of
the following is correct?
(a) For an
isochoric process, ∆ U = -q
(b) For an
adiabatic process, ∆ U =-w
(c) For an isothermal
process, q = + W
(d) For a cyclic
process, q = -w
Solution:
∆ U = q +w
For an isochoric process, w = -P∆ V =
0.Hence, ∆ U = qv
For an adiabatic
process, q = 0 .Hence, ∆ U = w
For an isothermal
process, q = -w .Hence, q = -w
For a cyclic
process, ∆ U = 0.Hence, q = -w
9. The
relation between ΔE and ΔH is
A) ΔH=ΔE−PΔV
B) ΔH=ΔE+PΔV
C) ΔE=ΔV+ΔH
D) ΔE=ΔH+PΔV
Solution:
ΔH
= ΔE + PΔV
10. For the
reaction N2+3H2⇌2NH3; ΔH=
A) ΔE−RT
B)
ΔE−2RT
C) ΔE+RT
D) ΔE+2RT
Solution:
ΔH = ΔE+ΔnRT
Since Δn = −2
then
ΔH = ΔE−2RT
11. The
work done during the expansion of a gas from a volume of 4dm3 to 6dm3 against a constant external pressure of 3atm is (1Latm=101.32J)
A) +304 J
B)
-304 J
C)
- 6 J
D)
-608 J
Solution:
W = −pΔV;
W = −3×(6−4)
W = −6×101.32 (∴1Latm=101.32J)
W = −608J
12. The work done in
ergs for the reversible expansion of one mole of an ideal gas from a volume of
10 litres to 20 litres
at 25°C is
A) 2.303×298×0.082log2
B) 298×107×8.31×2.303log2
C) 2.303×298×0.082log0.5
D) 8.31×107×298−2.303log0.5
Solution:
W = 2.303nRTlog
= 2.303×1×8.314×107×298log
= 298×107×8.314×2.303log2
|
|
|
|
