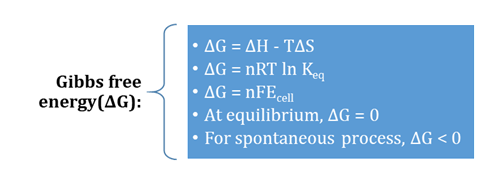
Gibbs Free Energy

It is another thermodynamic quantity that helps in predicting  the spontaneity of a process, earlier it was called as Gibbs free energy but according to IUPAC system, now it is simply called as Gibbs energy or Gibbs function. However the use of the term 'free energy' has not yet been completely stopped.

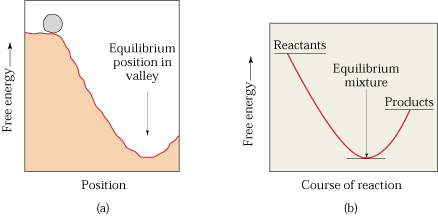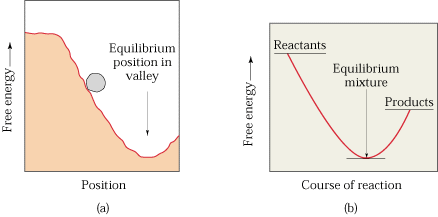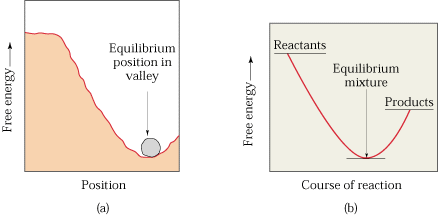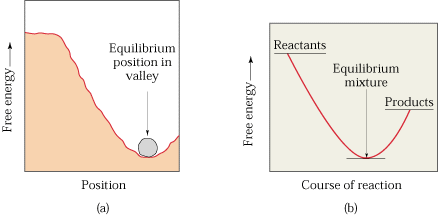
Image result for Gibbs Free Energy

Gibbs Free Energy Changes in Reactions

It is usually denoted by ‘G’ and is defined mathematically by the equation,

G=H-TS

where H is the heat content, T is the absolute temperature and S is the entropy of the system.

 As before, for the isothermal processes, we have

G1 = H1 – TS1 for the initial state

 G2 = H2 – TS2 for the final state

G2 - G1 = (H2 - H1) – T (S2-S1) or  ∆G=∆H - T∆S

where

∆G = G2 – G1 is the change in Gibbs's free energy of the system

∆H = H2 – H1 is the enthalpy change of the system and

∆S = S2 - S1 is the entropy change of the system.

The equation, ∆G=∆H-T∆S, is known as Gibbs-Helmoholtz equation (or simply Gibbs energy equation).

Spontaneity In Terms of Free Energy Change

(a) Deriving the criteria from entropy considerations

It has already been explained that the total entropy change when the system is not isolated from the surroundings is given by

∆Stotal = ∆Ssystem + ∆Ssurroundings                       ...(i)

Consider a process (or a reaction) being carried out at constant temperature and pressure. Suppose the heat is lost by the surroundings and gained by the system. If the heat lost by the surroundings is represented by qp (p indicating that the process is being carried out at constant pressure), then by definition of entropy change

∆Ssurroundings  =                                           ...(ii)

(minus sign before qp indicates that the heat is lost by the surroundings). Further, we know that at constant pressure,

qp =∆H                                                            ...(iii)

 

Substituting this value in eqn. (ii), we get

∆S surroundings =                                      ...(iv)

Substituting this value in eqn. (i), we get

∆S total =  ∆S system  -                                 ...(iv)

Using the symbol ∆S in place of ∆S system (being implied that  ∆S, stands for  ∆S for the system), we can write eqn. (iv) as

∆S total =  ∆S  -                                          ...(v)

Multiplying throughout by T, we get

T∆Stotal= T∆S – ∆H                                     …(vi)

But for a change taking place at constant temperature and pressure,

∆G=∆H - T∆S    ...(vii)

Substituting this value in eqn. (vi), we get

T∆Stotal = - ∆G or ∆G = - T∆Stotal              ...(viii)

But in terms of total entropy change, it has already been explained that

if ∆Stotal is positive, the process is spontaneous

if ∆S total is zero, the process is in equilibrium, and

if ∆Stotal, is negative, the direct process is non-spontaneous the reverse process may be spontaneous.

 Putting these results in eqn. (viii), it can be concluded that the criteria in terms of use for the spontaneity of the process will be as follows :

(i)                           If AG is negative, the process will be spontaneous.

(ii)                        If AG is zero, the process is in equilibrium.

(iii)                      If AG is positive, the direct process is non-spontaneous; the reverse process may be spontaneous.

An important advantage of free energy criteria over the entropy criteria lies in the fact that the rommet requires free energy change of the system only whereas the latter requires the total entropy change for the system and the surroundings.

(b) Deriving the criteria from Gibbs energy equation

According to Gibbs energy equation,

∆G=∆H - T∆S

This equation combines in itself both the factors which decide the spontaneity of a process, namely,

(i)                           the energy factor, ∆H

(ii)                        the entropy factor, T∆S

Thus, ∆G is the resultant of the energy factor (i.e., tendency for minimum energy) and the entropy factor (i.e., the tendency for maximum randomness).

Depending upon the signs of ∆H and  T∆S and their relative magnitudes, the following different possibilities arise :

       I.            When both ∆H and T∆S are negative, i.e., energy factor favours the process but randomness factor opposes it. Then

(i)                           If ∆H > T∆S the process is spontaneous and AG is negative.

(ii)                        If ∆H < T∆S, the process is non-spontaneous and AG is positive.

(iii)                      If ∆H= T∆S, the process is in equilibrium and AG is zero.

    II.            When both ∆H and T∆S are positive, i.e., energy factor opposes the process but randomness factor favours it. Then

(i)                           If ∆H > T∆S , the process is non-spontaneous and AG is positive.

(ii)                        If ∆H < T∆S , the process is spontaneous and AG is negative.

(iii)                      If ∆H = T∆S , the process is in equilibrium and AG is zero. III. When AH is negative but TAS is positive, i.e., energy factor as well as the randomness factor

 III.            When ∆His negative but T∆S is positive i.e., energy factor as well as randomness factor favour the process. The process will be highly spontaneous and ∆ G will be highly negative.

 IV.            When ∆H is positive but T∆S is negative, i.e., energy factors as well as the randomness factor oppose the process. The process will be highly non-spontaneous and AG will be highly positive.

To sum up, the criteria for spontaneity of a process in terms of AG is as follows:

(i)                           If AG is negative the process is spontaneous.

(ii)                        If AG is zero, the process does not occur or the system is in equilibrium.

(iii)                       If AG is positive the process does not occur in the forward direction. It may occur in the forward direction. It may occur in the backward direction.

Problems

1. Which of the following pairs of a chemical reaction is certain to result in spontaneous reaction?

A.  Exothermic and decreasing disorder

B.  Endothermic and increasing disorder

C.   Exothermic and increasing disorder

D.  Endothermic and decreasing disorder

Solution:

ΔG=ΔH−TΔS

 For spontaneous process ΔG should be negative in option (3) 

ΔH=−ve and ΔS=+ve then                 

ΔG= (−ve) −T (+ve)

 =−ve

 

2. Which of the following endothermic processes are spontaneous  

A.  Melting of ice   

B.  Evaporation of water

C.   Heat of combustion       

D.  Both A and B

Solution: 

Both Melting of ice   and Evaporation of water are spontaneous             

 

3. The free energy change for a reversible reaction at equilibrium is

A.  Large positive   

B.  Small negative

C.   Small positive   

D.  0

Solution:          

ΔG at equilibrium = 0.

 

4. For a spontaneous change, free energy change ΔG is

A.  Positive

B.  Negative

C.   Zero

D.  Can be positive or negative

Solution:         

For spontaneous change ΔG=−ve

 

5. A minus sign of the free energy change denotes that

A.  The reaction tends to proceed spontaneously

B.  The reaction is non-spontaneous

C.   The system is in equilibrium

D.  The reaction is very much unlikely

Solution:         

When ΔG=−ve than the reaction is spontaneous in nature.

 

6. The relation between ΔG and ΔH is

A.  ΔH=ΔG−TΔS            

B.  ΔG=ΔH−TΔS

C.   TΔS−ΔG=ΔH            

D.    ΔH=TΔG+ΔS

Solution:

The relation between ΔG and ΔH is  ΔG=ΔH−TΔS

 

7. The relation ΔG=ΔH−TΔS was given by [MP PMT 2000; KCET 2002]

A.  Boltzmann         

B.  Faraday

C.   Gibbs’Helmholtz            

D.  Thomson

Solution:

The relation ΔG=ΔH−TΔS was given by Gibbs’ Helmholtz            

 

8.  For precipitation reaction of Ag+ ions with NaCl, which of the following statements is correct?   

A.  ΔH for the reaction is zero

B.  ΔG for the reaction is zero

C.   ΔG for the reaction is negative

D.    [ΔG]=[ΔH]

Solution:         

Because the reaction is spontaneous.

 

9. At constant pressure and temperature, the direction to the result of any chemical reaction is where, there is less amount of

A.  Entropy               

B.  Enthalpy

C.   Gibb's free energy         

D.  None of the above

Solution:          

ΔG = -ve.

 

10. What is the free energy change ΔG when 1.0mole of water at 100°C and 1atm pressure is converted into steam t 100°C and 1atm pressure    

A.  540cal        

B.    −9800cal

C.     9800cal

D.    0cal

Solution:         

At equilibrium ΔG=0.

 

11. ΔG° for the reaction X+Y⇌ Z is - 4.606 kcal. The value of equilibrium constant of the reaction at 227°Cis (R=2.0cal.mol−1K−1)

A.  100

B.  10

C.   2             

D.  0.01

Solution:       

ΔG°=−2.303RTlogK           

 −4.606=−2.303×0.002×500 logK                                 

log k =2,

K=100.

 

12. Spontaneity of a chemical reaction is decided by the negative change

A.  Internal energy

B.  Enthalpy

C.   Entropy               

D.  Free energy

Solution:         

Spontaneous change shows ΔG=−ve

 

13. The essential condition for the feasibility of a reaction is that

A.  The reaction should be exothermic

B.  The entropy of products must be larger than that of reactants

C.   The reaction is to be accompanied with free energy decrease

D.  The reaction has to possess high activation energy

Solution:         

If  ΔG=−ve reaction is spontaneous.

 

14. The correct relationship between free energy change in a reaction and the corresponding equilibrium constant Kc is

A.  ΔG=RTlnKc       

B.    −ΔG=RTlnKc

C.   ΔGo=RTlnKc       

D.    −ΔGo=RTlnKc

Solution:

The correct relationship between free energy change in a reaction and the corresponding equilibrium constant Kc is −ΔGo=RTlnKc