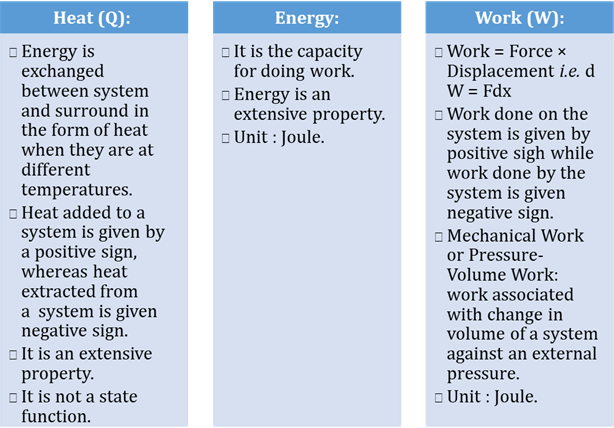
Internal Energy and Heat
Capacity
Internal energy
One of
the thermodynamic properties of a system is its internal energy, E,
which is the sum of the kinetic and potential energies of the particles that
form the system. The internal energy of a system can be understood by examining
the simplest possible system: an ideal gas. Because the particles in an ideal
gas do not interact, this system has no potential energy. The internal energy
of an ideal gas is therefore the sum of the kinetic energies of the particles
in the gas.
The
kinetic molecular theory assumes that the temperature of a gas is directly
proportional to the average kinetic energy of its particles, as shown in the
figure below.
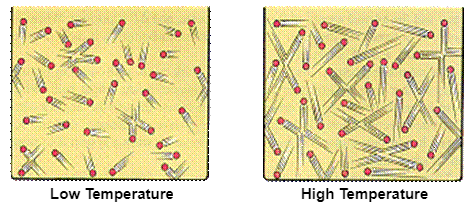
The internal energy of an ideal
gas is therefore directly proportional to the temperature of the gas.
Esys = 3/2 RT
In this equation, R is
the ideal gas constant in joules per mole kelvin (J/mol-K)
and T is the temperature in kelvin.
Heat capacity
Heat
capacity (c′) of a body is defined as the amount of heat energy
required to raise its temperature by 1 K.
![]()
The SI unit of heat
capacity is J![]() .
.
Specific heat capacity
Specific
heat capacity of a substance is defined as the amount of heat energy required
to raise the temperature of unit mass of the substance by 1 K.
c=![]()
Its SI unit is J![]()
Note: c=c′m where c′ is the heat capacity.
Specific heat capacity of common substances
|
Substance |
Specific heat capacity |
Specific heat capacity |
|
Mercury |
130 |
0.031 |
|
Copper |
399 |
0.095 |
|
Glass(flint) |
504 |
0.12 |
|
Aluminium |
882 |
0.21 |
|
Ice |
2100 |
0.50 |
|
Sea
water |
3900 |
0.95 |
|
water |
4180 |
1.0 |