Ideal and Non-ideal Solutions

Liquid-liquid solutions can be classified into ideal and non-ideal solutions on the basis of Raoult’s law.

Ideal Solutions:

The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions.

The ideal solutions have two important properties.

The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is also zero, i.e. Δ_mixH = 0 and Δ_mixV = 0 . It means that no heat is absorbed or evolved when the components are mixed. Also, the volume of solution would be equal to the sum of volumes of the two components.

At molecular level, ideal behaviour of the solutions can be explained by considering two components A and B. In pure components, the intermolecular attractive interactions will be of types A-A and B-B, whereas in the binary solutions in addition to these two interactions, A-B type of interactions will also be present.

If the intermolecular attractive forces between the A-A and B-B are nearly equal to those between A-B, this leads to the formation of ideal solution.

A perfectly ideal solution is rare but some solutions are nearly ideal in behaviour. Solution of n-hexane and n-heptane, bromoethane and chloroethane, benzene and toluene, chlorobenzene and bromobenzene etc. fall into this category. Most of the dilute solutions behave as ideal solutions.

Ideal solutions

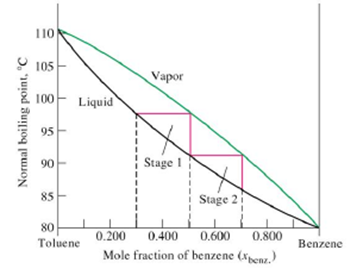
Notes:

Ø The process of separation of one liquid from another liquid (binary mixture) having different boiling points by distillation is called fractional distillation.

Ø The separation is possible when the vapour phase has a different composition from that boiling liquid mixture.

Ø Thus the components of ideal solution can be separated by fractional distllation.

Examples of ideal solutions:

Ø All dilute solutions

Ø benzene + toluene

Ø n-hexane + n- heptane

Ø clorobenzene + bromobenzene

Ø ethyl bromide + ethyl iodide

Ø n-butyl chloride + n-butyl bromide

Non-ideal Solutions:

When a solution does not obey Raoult’s law over the entire range of concentration, then it is called non-ideal solution.

The vapour pressure of such a solution is either higher or lower than that predicted by Raoult’s law. If it is higher, the solution exhibits positive deviation and if it is lower, it exhibits negative deviation from Raoult’s law.

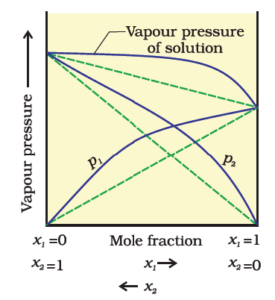
Positive Deviation:

The cause for these deviations lie in the nature of interactions at the molecular level. In case of positive deviation from Raoult’s law, A-B interactions are weaker than those between A-A or B-B, i.e.

In this case the intermolecular attractive forces between the solute-solvent molecules are weaker than those between the solute-solute and solvent-solvent molecules. This means that in such solutions, molecules of A (or B) will find it easier to escape than in pure state. This will increase the vapour pressure and result in positive deviation.

Mixtures of ethanol and acetone behave in this manner. In pure ethanol, molecules are hydrogen bonded. On adding acetone, its molecules get in between the host molecules and break some of the hydrogen bonds between them. Due to weakening of interactions, the solution shows positive deviation from Raoult’s law.

Positive Deviation

In a solution formed by adding carbon disulphide to acetone, the dipolar interactions between solute-solvent molecules are weaker than the respective interactions among the solute-solute and solvent-solvent molecules. This solution also shows positive deviation.

For solution showing positive deviation from Rault’s law Δ_mixH > 0 and Δ_mixV > 0,

Examples of solutions showing positive deviation from Rault’s law

Ø acetone + ethanol

Ø acetone + CS₂

Ø water + methanol

Ø water + ethanol

Ø CCl₄ + toluene

Ø CCl₄ + CHCl₃

Ø acetone + benzene

Ø CCl₄+ CH₃OH

Ø cycloheane + methanol

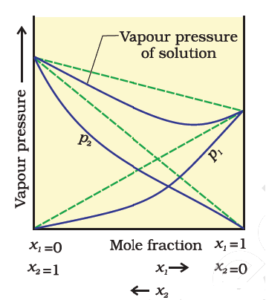
Negative Deviation:

In case of negative deviations from Raoult’s law, the intermolecular attractive forces between A-A and B-B are weaker than those between A-B and leads to decrease in vapour pressure resulting in negative deviations.

An example of this type is a mixture of phenol and aniline. In this case the intermolecular hydrogen bonding between phenolic proton and lone pair on nitrogen atom of aniline is stronger than the respective intermolecular hydrogen bonding between similar molecules. Similarly, a mixture of chloroform and acetone forms a solution with negative deviation from Raoult’s law. This is because chloroform molecule is able to form hydrogen bond with acetone molecule as shown.

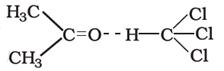
Hydrogen Bonding

This decreases the escaping tendency of molecules for each component and consequently the vapour pressure decreases resulting in negative deviation from Raoult’s law.

Negative Deviations

For solution showing positive deviation from Rault’s law Δ_mixH < 0 and Δ_mixV < 0,

Examples of solutions showing negative deviation from Rault’s law

Ø acetone + aniline

Ø acetone + chloroform

Ø methanol + acetic acid

Ø water + nitric acid

Ø chloroform + diethyl ether

Ø water + HCl

Ø acetic acid + pyridine

Ø chloroform + benzene

Ideal solutions

Non-ideal solutions

Positive deviation from Raoult's law

Negative deviation from Raoult's law

1.Obey Raoult's law at every range of concentration.

1.Do not obey Raoult's law.

1. Do not obey Raoult's law.

2.ΔHmix=0;

neither heat is evolved nor absorbed during dissolution.

2.ΔHmix>0.

Endothermic dissolution; heat is absorbed.

2.ΔHmix<0.

Exothermic dissolution; heat is evolved.

3.ΔVmix=0;

total volume of solution is equal to sum of volumes of the components.

3.ΔVmix>0.

Volume is increased after dissolution.

3.ΔVmix<0.

Volume is decreased during dissolution.

4.P=pA+pB=p0AXA+p0BXB

i.e.,pA=p0AXA:pB=p0BXB

4.pA>p0AXA;

pB>p0BXB

∴pA+pB>p0AXA+p0BXB

4.pA<p0AXA;

pB<p0BXB

∴pA+pB<p0AXA+p0BXB

5.A−A, A−B, B−B

interactions should be same, i.e., 'A' and 'B' are identical in shape, size and character.

5.A−B

attractive force should be weaker than A−A and B−B attractive forces. 'A' and 'B' have different shape, size and character.

5.A−B

attractive force should be greater than A−A and B−B attractive forces. 'A' and 'B' have different shape, size and character.

6. Escaping tendency of 'A' and 'B' should be same in pure liquids and in the solution.

6. 'A' and 'B' escape easily showing higher vapour pressure than the expected value.

6. Escaping tendency of both components 'A' and 'B' is lowered showing lower vapour pressure than expected ideally.

Examples:

Dilute solutions;

benzene + toluene:

n-hexane + n-heptane;

chlorobenzene + bromobenzene;

ethyl bromide + ethyl iodide;

n-butyl chloride + n-butyl bromide

Examples:

Acetone +ethanol

acetone +CS2;

water + methanol;

water + ethanol;

CCl4+toluene;

CCl4+CHCl3;

acetone + benzene;

CCl4+CH3OH;

cyclohexane + ethanol

Examples:

Acetone + aniline;

acetone + chloroform;

CH3OH + CH3COOH;

H2O + HNO3;

chloroform + diethyl ether;

water + HCl;

acetic acid + pyridine;

chloroform + benzene

Azeotropes:

Azeotropes are binary mixtures having the same composition in liquid and vapour phase and boil at a constant temperature.

Some liquids on mixing, form azeotropes. In such cases, it is not possible to separate the components by fractional distillation. There are two types of azeotropes called minimum boiling azeotrope and maximum boiling azeotrope.

The solutions which show a large positive deviation from Raoult’s law form minimum boiling azeotrope at a specific composition.

For example, ethanol-water mixture (obtained by fermentation of sugars) on fractional distillation gives a solution containing approximately 95% by volume of ethanol. Once this composition, known as azeotrope composition, has been achieved, the liquid and vapour have the same composition, and no further separation occurs.

The solutions that show large negative deviation from Raoult’s law form maximum boiling azeotrope at a specific composition. Nitric acid and water is an example of this class of azeotrope. This azeotrope has the approximate composition, 68% nitric acid and 32% water by mass, with a boiling point of 393.5 K.