Conductance of Electrolytic Solutions

Resistance of a cell

The resistance R of a cell depends

i. Directly on the length of column (distance between the electrodes) of solution, l i.e.

R ∝ l

ii. Inversely on area of cross-section A of the electrode plates, i.e.

R ∝

iii. On the nature of the electrolyte

On combining the above factors, we get

R = ρ ×

The proportionality constant ρ (Rho) is called resistivity of electrolyte.

R can be calculated using wheat stone bridge.

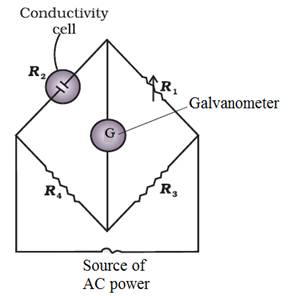
When the Wheatstone bridge is balanced

R₂ =

Conductance of a cell

It is the ease of flow of electric current through the conductor. It is reciprocal of resistance (R).

G =

=

= κ ×

where,

κ = , is called the conductivity

The SI unit of conductance is siemens, represented by the symbol ‘S’ and is equal to ohm–1 (also known as mho) or Ω–1.

Conductivity of a cell (κ)

The inverse of resistivity is called conductivity or specific conductance. It is represented by the symbol, κ (Greek, kappa).

κ =

=

= G ×

κ = G × G*

= 

where,

G* =  is called the cell constant

The SI unit is S m-1

Unit of cell constant is cm-1 or m-1.

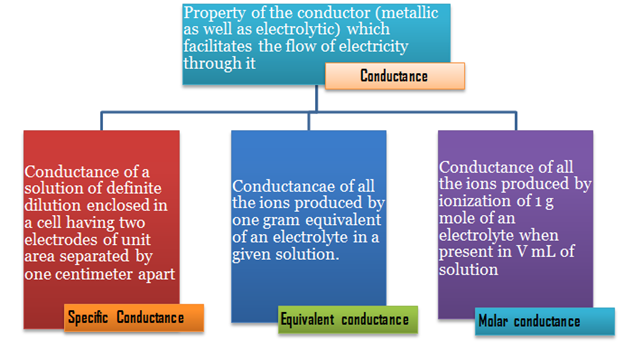
Molar conductivity of a solution (Λ_m)

Molar conductivity of a solution at a given concentration is defined as,

Λ_m =

= 

where

M = molarity

c = concentration in mole per m³

The unit of molar conductivity is Ω^-1 cm² mol^-1 or S cm² mol^-1.

1 S m² mol^–1 = 10⁴ S cm² mol^–1

or 1 S cm² mol^–1 = 10^–4 S m² mol^–1.

Factors affecting conductivity

i. Nature of electrolyte - The strong electrolytes like KNO₃, KCl, NaOH etc. are completely ionised in aqueous solution and have high values of molar conductivity.

The weak electrolytes are ionised to a lesser extent in aqueous solution and have lower values of molar conductivity.

ii. Concentration of the solution - The concentrated solutions of strong electrolytes have significant interionic attractions, which reduce the speed of ions and lower the value of Λ_m.

As the dilution decreases such attractions also decrease which increases the value of Λ_m.

iii. Temperature - The increase of temperature decreases inter-ionic attractions and increases kinetic energy of ions and their speed. Thus, Λ_m and Λeq increase with temperature.

iv. Size of the ions produced and their solvation.

v. The nature of the solvent and its viscosity. Higher the viscosity, lower is conductivity

Variation of conductivity and molar conductivity with concentration

Conductivity of strong electrolytes

For strong electrolytes, Λ_m increases slowly with dilution and is given by,

Λ_m=  − A√C

If we plot Λ_m against √C, we obtain a straight line with intercept equal to  and slope equal to ‘–A’. The value of ‘A’ for a given solvent and temperature depends on the type of electrolyte i.e., the charges on the cation and anion produced on the dissociation of the electrolyte in the solution.

The limiting value,  (the molar conductivity at zero concentration or at infinite dilution) can be obtained extrapolating the graph.

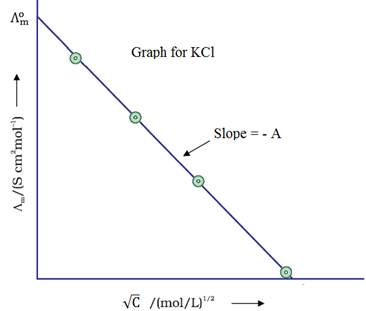
Depending upon the type of ions involved, NaCl, CaCl₂, MgSO₄ are known as 1-1, 2-1 and 2-2 electrolytes respectively.

All electrolytes of a particular type have the same value for ‘A’.

Conductivity of weak electrolytes

For weak electrolytes like acetic acid, Λ_m increases steeply on dilution, especially near lower concentrations. This is because they have lower degree of dissociation at higher concentrations and hence for such electrolytes, the change in Λ_m with dilution is due to increase in the degree of dissociation and consequently the number of ions in total volume of solution that contains 1 mol of electrolyte.

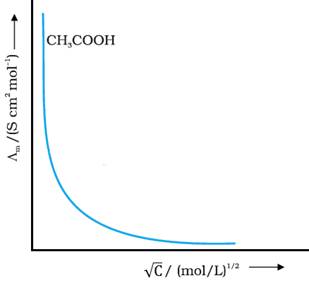
Therefore,  cannot be obtained by extrapolation of  to zero concentration.

At infinite dilution (i.e., concentration c → zero) electrolyte dissociates completely (α = 1), but at such low concentration the conductivity of the solution is so low that it cannot be measured accurately.

Therefore,  for weak electrolytes is obtained by using Kohlrausch’s law of independent migration of ions.