Integrated Rate Equation

The concentration dependence of rate is called differential rate equation. It is not always convenient to determine the instantaneous rate, as it is measured by determination of slope of the tangent at point, t in concentration vs time plot. This makes it difficult to determine the rate law and hence the order of the reaction.

If we integrate the differential rate equation to give a relation between directly measured experimental data, i.e., concentrations at different times and rate constant, the equation obtained is called integrated rate equation.

The integrated rate equations are different for the reactions of different reaction orders.

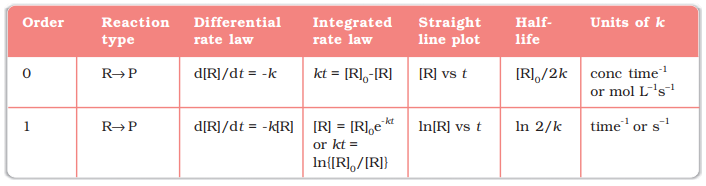
Zero order reactions

The rate of the reaction is proportional to zero power of the concentration of reactants.

Consider the reaction, R → P

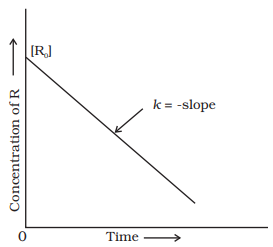
Integrating both sides, we get,

[R] = – k t + C

where, C is the constant of integration.

Now, at t = 0, the concentration of the reactant R = [R_o] = initial concentration of the reactant.

Substituting the value, we get,

[R_o] = –k × 0 + C

[R_o] = C

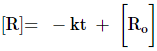
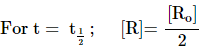
For zero order gaseous reactions,

Example

Rate = k[NH₃]⁰ = k

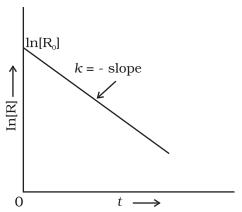
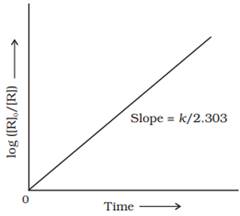
First order reactions

The reaction, whose rate is proportional to the concentration of reactants, is called first order reaction.

R → P

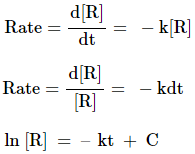
When t = 0, R = [R_o], where [R_o] is the initial concentration of the reactant.

Therefore,

ln [R_o] = – k × 0 + C

ln [R_o] = C

Substituting the value of C

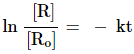
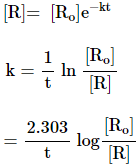
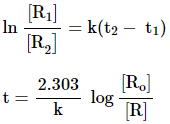
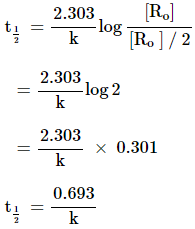
Ø For zero order reaction, t_½ ∝ [R]_o.

Ø For first order reaction t_½ is independent of [R]_o.

For first order gas phase reaction of type

A(g) → B(g) + C(g)

Let p_i be the initial pressure of A and p_t the total pressure at time ‘t’.

Total pressure p_t = p_A + p_B + p_C (pressure units)

If x atm be the decrease in pressure of A at time t and one mole each of B and C is being formed, the increase in pressure of B and C will also be x atm each.

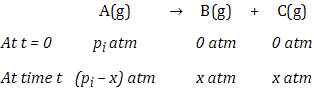
Now

p_t = (p_i – x) + x + x

= p_i + x

x = (p_t - p_i)

where,

p_A = p_i – x = p_i – (p_t – p_i)

p_A = 2p_i – p_t

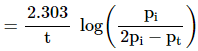
Example:

Hydrogenation of ethene is an example of first order reaction.

C₂H₄(g) + H₂ (g) → C₂H₆(g)

Rate = k [C₂H₄]

All natural and artificial radioactive decay of unstable nuclei take place by first order kinetics.

Rate = k [Ra]

Half life of reaction (t_1/2)

The time in which the concentration of a reactant is reduced to one half of its initial concentration.

Eg: For a Zero Order reaction t_1/2 =

Eg: For a first order reaction t_1/2 = log2 =

Pseudo first order reaction

Chemical reactions which appear to be of higher order but actually are of the lower order are called pseudo order reactions. In case of pseudo first order reaction, chemical reaction between two substances takes place when one of the reactants is present in excess, e.g., hydrolysis of ester.

Example – Hydrolysis of ethyl acetate

During the hydrolysis of 0.01 mol of ethyl acetate with 10 mol of water, amounts of the various constituents at the beginning (t = 0) and completion (t) of the reaction are given as under.

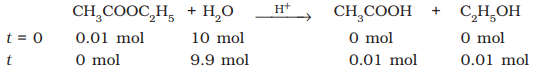
The concentration of water does not get altered much during the course of the reaction.

So, in the rate equation

Rate = k′ [CH₃COOC₂H₅] [H₂O]

the term [H₂O] can be taken as constant.

The equation, thus, becomes

Rate = k [CH₃COOC₂H₅]

where k = k′ [H₂O] and the reaction behaves as first order reaction.

A reaction in which concentration of one of the reactants can be taken as constant and can be included in the rate constant, are called pseudo first order reactions.

For first order chemical reaction of type,

where V_o, V_t, and V_∞ are the volumes of NaOH solution used for the titration of same volume of the reaction mixture after times 0, t and ∞ respectively.

Inversion of cane sugar is another pseudo first order reaction.

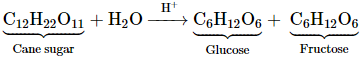
Rate = k [C₁₂H₂₂O₁₁]

Also

where r_o, r_t, and r_∞ are the polarimetric readings (angle of rotation of polarized light) at t = 0, t and ∞, respectively.

Comparison of zero and first order rections