Beats

‘Beats’ is an interesting phenomenon arising from interference of waves. When two harmonic sound waves of close (but not equal) frequencies are heard at the same time, we hear a sound of similar frequency (the average of two close frequencies), but we hear something else also. We hear audibly distinct waxing and waning of the intensity of the sound, with a frequency equal to the difference in the two close frequencies. Artists use this phenomenon often while tuning their instruments with each other. They go on tuning until their sensitive ears do not detect any beats.

To see this mathematically, let us consider two harmonic sound waves of nearly equal angular frequency ω₁ and ω₂ and fix the location to be x = 0 for convenience. Eq. y(x, t) = a sin(kx – ω t + φ) with a suitable choice of phase (φ = π/2 for each) and, assuming equal amplitudes, gives

s₁ = a cos ω₁ t and s₂ = a cos ω₂ t (1)

Here we have replaced the symbol y by s, since we are referring to longitudinal not transverse displacement. Let ω₁ be the (slightly) greater of the two frequencies. The resultant displacement is, by the principle of superposition,

s = s₁ + s₂ = a (cosω₁ t + cos ω₂ t)

Using the familiar trignometric identity for cos A + cos B, we get

= 2 a cos cos (2)

which may be written as :

s = [2 a cos ω_b t] cos ω_a t (3)

If |ω₁ – ω₂ | <<ω1 , ω2 , ωa >< ω₁, ω₂, ω_a >> ω_b, t

where

ω_b = and ω_a =

Now if we assume |ω₁ – ω₂ | <<ω1 ,which means>< ω₁ which means ω_a >> ω_b , we can interpret Eq. (3) as follows. The resultant wave is oscillating with the average angular frequency ω_a ; however its amplitude is not constant in time, unlike a pure harmonic wave. The amplitude is the largest when the term cos ω_b t takes its limit +1 or –1. In other words, the intensity of the resultant wave waxes and wanes with a frequency which is 2ω_b = ω₁ – ω₂ . Since ω = 2πν, the beat frequency ν_beat, is given by

νbeat = ν₁ – ν₂ (15.48)

Below figure illustrates the phenomenon of beats for two harmonic waves of frequencies 11 Hz and 9 Hz. The amplitude of the resultant wave shows beats at a frequency of 2 Hz.

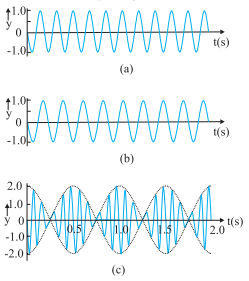
Superposition of two harmonic waves, one of frequency 11 Hz (a), and the other of frequency 9Hz (b), giving rise to beats of frequency 2 Hz, as shown in (c).