Reflection of Waves

We encounter situations involving the reflection of waves all around us, for example, in the phenomenon of echo, the sound reflected from a distant object reaches the listener with a little delay. In this section, we will learn more about the reflection of a wave from a fixed and a free end.

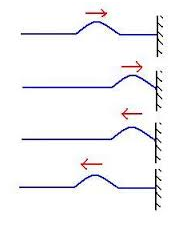
In the image shown below, we can see what happens when a pulse or a travelling wave encounters a rigid boundary. We see how under such a situation the pulse or the wave gets reflected.

When a wave is an incident on any surface, a part of the incident wave is reflected and a part is transmitted into the second medium. If the wave is incident obliquely on the boundary, the transmitted wave can also be termed as a reflected wave.

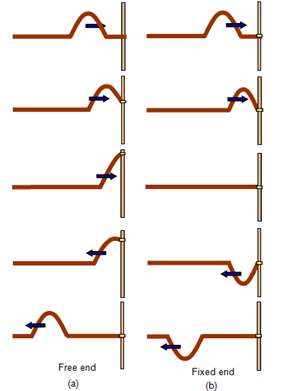
Here, the incident and the refracted waves obey Snell’s law of refraction and the incident and the reflected waves obey the laws of reflection. The reflection of wave or a pulse can happen from two types of surfaces, it can either be a fixed wall or a ring, as shown in the image below.

Fixed end reflection

Let us consider the situation where a string is fixed to a rigid wall at its right end. When we allow a pulse to propagate through these strings, the pulse reaches the right end, gets reflected as shown in the figure above. When the pulse arrives at the fixed end, it exerts a force on the wall and according to Newton’s third law, the wall exerts an equal and opposite force on the string. This second force generates a pulse at the support, which travels back along the string in the direction opposite to that of the incident pulse. In a reflection of this kind, there is no displacement at the support as the string is fixed there. The reflected and incident pulses have opposite signs and they cancel each other at that point. Thus, in case of a travelling wave, the reflection at a rigid boundary takes place with a phase reversal or with a phase difference of π.

Free end reflection

When the right end of the string is tied to a ring, which slides up and down without any friction on a rod, we term it as a free end.  In this case, when the pulse arrives at the right end, the ring moves up the rod and as it moves, it pulls on the string, stretching the string and producing a reflected pulse with the same sign and amplitude as the incident pulse. Thus, in such a reflection, the incident and reflected pulses reinforce each other, creating the maximum displacement at the end of the string: the maximum displacement of the ring is twice the amplitude of either of the pulses. Thus, the reflection occurs without any additional phase shift. In case of a travelling wave the reflection at an open boundary the reflection takes place without any phase change.

Summarizing the above result, we can say that the reflection of waves at a boundary between two media takes place accordingly. A travelling wave, at a rigid boundary or a closed end, is reflected with a phase reversal but the reflection at an open boundary takes place without any phase change.

Mathematically, if the incident wave is represented as y_i(x, t) = a sin (kx – ωt), then, for reflection at a rigid boundary, the reflected wave is represented by

y_r (x, t) = a sin (kx + ωt + π). = – a sin (kx + ωt)

And when the wave gets reflected at an open boundary, the reflected wave is represented by

y_r (x, t) = a sin (kx + ωt).