Simple Harmonic Motion

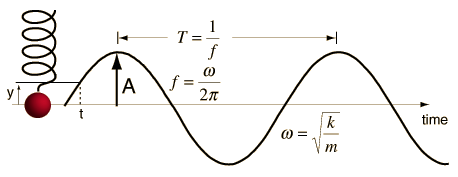
Any motion that repeats itself after regular intervals of time is known as a periodic motion.

If a body moves back and forth repeatedly about a mean position, it is said to possess oscillatory motion. Vibrations of guitar strings, motion of a pendulum bob, vibrations of a tuning fork, oscillations of mass suspended from a spring, vibrations of diaphragm in telephones and speaker system and freely suspended springs are few examples of oscillatory motion. In all the above cases of vibrations of bodies, the path of vibration is always directed towards the mean or equilibrium position.

The oscillations can be expressed in terms of simple harmonic functions like sine or cosine function. A harmonic oscillation of constant amplitude and single frequency is called simple harmonic motion (SHM).

Equation of motion for simple harmonic motion

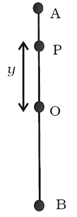
A particle is said to execute simple harmonic motion if its acceleration is directly proportional to the displacement from a fixed point and is always directed towards that point.

Consider a particle P executing SHM along a straight line between A and B about the mean position O as shown in figure. The acceleration of the particle is always directed towards a fixed point on the line and its magnitude is proportional to the displacement of the particle from this point.

(i.e) a α y

By definition a = −ω² y

where ω is a constant known as angular frequency of the simple harmonic motion. The negative sign indicates that the acceleration is opposite to the direction of displacement. If m is the mass of the particle, restoring force that tends to bring back the particle to the mean position is given by

F = −m ω² y

or F = −k y

The constant k = m ω², is called force constant or spring constant. Its unit is N m⁻¹. The restoring force is directed towards the mean position.

Thus, simple harmonic motion is defined as oscillatory motion about a fixed point in which the restoring force is always proportional to the displacement and directed always towards that fixed point.

The projection of uniform circular motion on a diameter is SHM

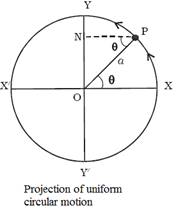
Consider a particle moving along the circumference of a circle of radius a and centre O, with uniform speed v, in anticlockwise direction as shown in figure. Let XX^’   and YY^’   be the two perpendicular X^/ diameters.

Suppose the particle is at P after a time t. If ω is the angular velocity, then the angular displacement θ in time t is given by θ = ωt.

From P draw PN perpendicular to YY ^’ . As the particle moves from X to Y, foot of the perpendicular N moves from O to Y. As it moves further from Y to X ^’, then from X ^’ to Y ^’ and back again to X, the point N moves from Y to O, from O to Y ′ and back again to O. When the particle completes one revolution along the circumference, the point N completes one vibration about the mean position O. The motion of the point N along the diameter YY ^’ is simple harmonic.

Hence, the projection of a uniform circular motion on a diameter of a circle is simple harmonic motion.

Displacement in SHM

The distance travelled by the vibrating particle at any instant of time t from its mean position is known as displacement. When the particle is at P, the displacement of the particle along Y axis is y as shown in figure.

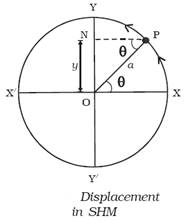
Then, in ∆ OPN, sin θ = ON/OP

ON = y = OP sin θ

y = OP sin ωt (θ = ωt)

Since OP = a, the radius of the circle, the displacement of the vibrating particle is

y = a sin ωt             …... (1)

The amplitude of the vibrating particle is defined as its maximum displacement from the mean position.

Velocity in SHM

The rate of change of displacement is the velocity of the vibrating particle.

Differentiating eqn. (1) with respect to time t

dy/dt = d/dt (a sin ωt)

So, v = aω cos ωt          …...(2)

The velocity v of the particle moving along the circle can also be obtained by resolving it into two components as shown in figure.

(i) v cos θ in a direction parallel to OY 

(ii) v sin θ in a direction perpendicular to OY.

The component v sin θ has no effect along YOY ′ since it is perpendicular to OY.

So, velocity = v cos θ = v cos ωt

We know that, linear velocity = radius × angular velocity

So, v = aω

Thus, Velocity = aω cos ωt

Or, Velocity = aω √1- sin²ωt

Velocity = aω √1- (y/a)²       (Since, sin θ = y/a)

Velocity = ω √a²- y²         …... (3)

Special Cases

(a) When the particle is at mean position, (i.e) y = 0. Velocity is aω and is maximum. v = + aω is called velocity amplitude.

(b) When the particle is in the extreme position, (i.e) y = + a, the velocity is zero.

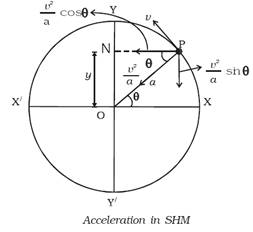
Acceleration in SHM

The rate of change of velocity is the acceleration of the vibrating particle.

d²y/dt² = d/dt (dy/dt) = d/dt (aω cos ωt) = -ω² a sin ωt

Thus, acceleration = d²y/dt² = – ω²y         …... (4)

The acceleration of the particle can also be obtained by component method.

The centripetal acceleration of the particle P acting along PO is v²/a. This acceleration is resolved into two components as shown in figure.

(a) v²/a (cos θ) along PN perpendicular to OY.

(b) v²/a (sin θ) in a direction parallel to YO.

The component v²/a (cos θ) has no effect along YOY' since it is perpendicular to OY.

Hence acceleration = – v²/a (sin θ)

= – aω²sin ωt         (Since, v = aω)

= – ω²y                (Since, y = a sin ωt)

So, acceleration = –  ω²y

The negative sign indicates that the acceleration is always opposite to the direction of displacement and is directed towards the centre.

Special Cases

(a) When the particle is at the mean position (i.e) y = 0, the acceleration is zero.

(b) When the particle is at the extreme position (i.e) y = +a, acceleration is ∓ a ω² which is called as acceleration amplitude.

The differential equation of simple harmonic motion from eqn. (4) is

+ y = 0           …... (5)

It will be clear from the above, that at the mean position y = 0, velocity of the particle is maximum but acceleration is zero. At extreme position y = +a, the velocity is zero, but the acceleration is maximum ∓ a ω² acting in the opposite direction.