Addition and Subtraction of Vectors

Addition of vectors:

Vectors by definition, obey the triangle law or equivalently, the parallelogram law of addition. We shall now describe this law of addition using the graphical method.

Let us consider two vectors  and  that lie in a plane as shown in below figure.

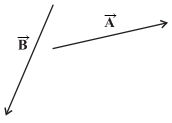
kinsm8.PNG

Vectors  and

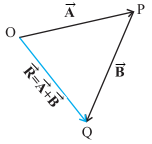
The lengths of the line segments representing these vectors are proportional to the magnitude of the vectors. To find the sum  + , we place vector  so that its tail is at the head of the vector , as in below figure. 

Vectors  and  added graphically

Then, we join the tail of  to the head of . This line OQ represents a vector , that is, the sum of the vectors  and . Since, in this procedure of vector addition, vectors are arranged head to tail, this graphical method is called the head-to-tail method.

The two vectors and their resultant form three sides of a triangle, so this method is also known as triangle method of vector addition. 

Vectors  and  added graphically

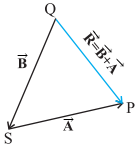
If we find the resultant of  +  as in above figure, the same vector  is obtained. Thus, vector addition is commutative:

 +   +                   ------ (1)

The addition of vectors also obeys the associative law as illustrated in below figure. 

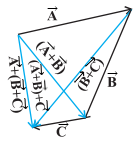
Illustrating the associative law of vector addition

The result of adding vectors  and  first and then adding vector  is the same as the result of adding  and  first and then adding vector  :

 ( + ) +  + ( + )        ------ (2)

What is the result of adding two equal and opposite vectors ? 

Consider two vectors  and  shown in below figure.

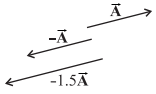
kinsm7.PNG

Their sum is  + (–). Since the magnitudes of the two vectors are the same, but the directions are opposite, the resultant vector has zero magnitude and is represented by 0 called a null vector or a zero vector :

 –        ||0     ------ (3)

Since the magnitude of a null vector is zero, its direction cannot be specified.

The null vector also results when we multiply a vector  by the number zero. The main properties of  are :

 +  

     λ  

    0                             ------ (4)

What is the physical meaning of a zero vector?

Consider the position and displacement vectors in a plane as shown in below figure.

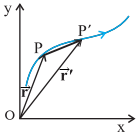
Now suppose that an object which is at P at time t, moves to P′ and then comes back to P.

Then, what is its displacement? Since the initial and final positions coincide, the displacement is a “null vector”. 

Subtraction of vectors:

Subtraction of vectors can be defined in terms of addition of vectors. We define the difference of two vectors  and  as the sum of two vectors  and – :

 –  + (–)             ------ (5)

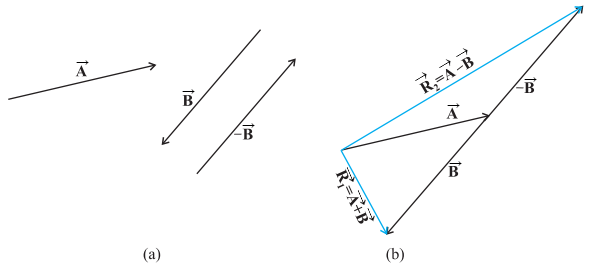
(a) Two vectors  and , –is also shown.
(b) Subtracting vector  from vector  – the result is . For comparison, addition of vectors  and , i.e.  is also shown.

It is shown in above figure. The vector – is added to vector  to get  = ( – ). The vector  =  +  is also shown in the same figure for comparison.

We can also use the parallelogram method to find the sum of two vectors. Suppose we have two vectors  and . To add these vectors, we bring their tails to a common origin O as shown in below figure. 

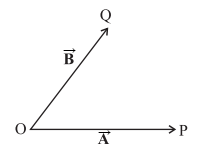
Two vectors  and  with their tails brought to a common origin

Then we draw a line from the head of  parallel to  and another line from the head of  parallel to  to complete a parallelogram OQSP. Now we join the point of the intersection of these two lines to the origin O. The resultant vector  is directed from the common origin O along the diagonal (OS) of the parallelogram as shown in below figure.

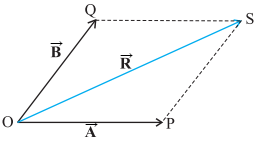
The sum  +  obtained using the parallelogram method

In below figure, the triangle law is used to obtain the resultant of  and  and we see that the two methods yield the same result. Thus, the two methods are equivalent.

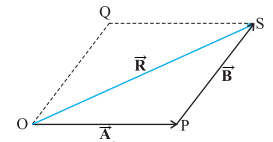
The parallelogram method of vector addition is equivalent to the triangle method