Relative Velocity

You must be familiar with the experience of travelling in a train and being overtaken by another train moving in the same direction as you are. While that train must be travelling faster than you to be able to pass you, it does seem slower to you than it would be to someone standing on the ground and watching both the trains. In case both the trains have the same velocity with respect to the ground, then to you the other train would seem to be not moving at all.

To understand such observations, we now introduce the concept of relative velocity.

Consider two objects A and B moving uniformly with average velocities  and  in one dimension, say along -axis. If (0) and (0) are positions of objects A and B, respectively at time t  0, their positions (t) and (t) at time t are given by:

(t)    (0) +  t                                                                     ------ (1a)

(t)    (0) +  t                                                                    ------ (1b)

Then, the displacement from object A to object B is given by

          (t)    (t) – (t)

   [(0) – (0)] + ( – ) t                                     ------ (2)

Equation (2) is easily interpreted. It tells us that as seen from object A, object B has a velocity  –  because the displacement from A to B changes steadily by the amount  –  in each unit of time. We say that the velocity of object B relative to object A is  –  :

        –                                                                              ------ (3a)

Similarly, velocity of object A relative to object B is:

        –                                                                              ------ (3b)

This shows:      –                                                                                  ------ (3c)

Now we consider some special cases :

(a) If    ,  –     0. Then, from Eq. (2), (t) – (t)    (0) – (0). Therefore, the two objects stay at a constant distance ((0) – (0)) apart, and their position–time graphs are straight lines parallel to each other as shown in below figure. The relative velocity  or  is zero in this case.

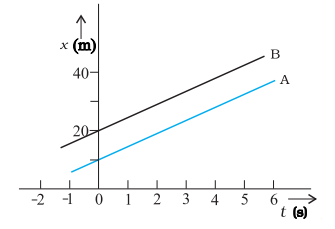
kinsm48.PNG

Position-time graphs of two objects with equal velocities.

(b) If  > ,  –  is negative. One graph is steeper than the other and they meet at a common point. For example, suppose     20 m s-1 and (0)    10 m; and     10 m s-1, (0)    40 m; then the time at which they meet is t    3 s (below figure). At this instant they are both at a position (t)    (t)    70 m. Thus, object A overtakes object B at this time. In this case, 

       10 m s–1 – 20 m s–1 

  – 10 m s–1 

  – 

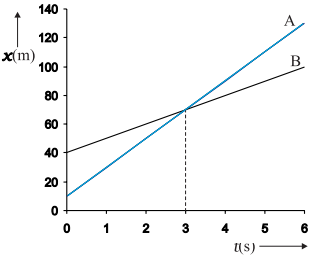
kinsm49.PNG

Position-time graphs of two objects with unequal velocities, showing the time of meeting.

(c) Suppose  and  are of opposite signs. For example, if in the above example object A is moving with 20 m s–1 starting at (0)    10 m and object B is moving with – 10 m s–1 starting at (0)    40 m, the two objects meet at t    1 s (below figure).

The velocity of B relative to A, 

       [–10 – (20)] m s–1 

  –30 m s–1 

  –  

In this case, the magnitude of  or  (30 m s–1) is greater than the magnitude of velocity of A or that of B. If the objects under consideration are two trains, then for a person sitting on either of the two, the other train seems to go very fast.

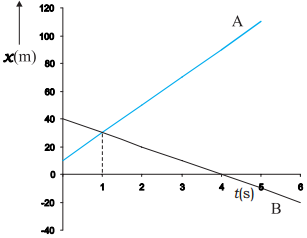
kinsm50.PNG

Position-time graphs of two objects with velocities in opposite directions, showing the time of meeting.

Note that Eq. (3) are valid even if  and  represent instantaneous velocities.

Problems:

1. A car A moving at 10 m/s on a straight road, is ahead of car B moving in same direction at 6 m/s. Find the velocity of A relative to B.

Solution:

Here,

     10 m/s,    6 m/s

                 

                     10 m/s  6 m/s

                     4 m/s

              4 m/s

Positive Velocity indicates that the driver of car B sees car A moving ahead from him at the rate of 4 m/s.

 

2. Two trains 120 m and 80 m in length are running opposite direction with velocity 42 km/h and 30 km/h. In what time they will completely cross each other?

Solution:

Distance    Lengths of the two trains

         120 + 80 m

         200m

 Velocity    42 + 30

         72 Km/hr

         20m/s (velocities are added since they are in opposite direction)

       Time   

          

         10 seconds

 

3. The speed of a motor launch with respect to still water is 7 m/s and the speed of the stream is 3 m/s. When the launch began travelling upstream, a float was dropped from it. The launch travelled 4.2 km upstream, turned about and caught up with the float. How long is it before the launch reaches the float?

Solution:

For upstream motion of launch:

Relative velocity         7 – 3

      4 m/s

Distance moved          4.2 km

     4200 m

Time taken,           

     1050 s

For downstream motion of launch:

Distance moved downstream by float in 1050 s

     3 × 1050

     3150 m

Distance between float and launch turned about

     4200 + 3150

     7350 m

This distance covered by launch with its own velocity (7 m/s) because stream velocity is being shared by both

∴ Time taken,            

     1050 s

Total time taken,  

     1050 + 1050

     2100 s

     35 min

 

4. A motorboat covers the distance between two spots on the river in 8 h and 12 h downstream and upstream respectively. What is the time required for motor boat to cover this distance in still water?

Solution:

Let  and  be the velocity of boat in still water and velocity of river respectively. If  is the distance between the two spots, then

        (for upstream)

      (for downstream)

On adding,

           or     

Time required by boat in still water

           

             

                9.6 h

 

5. A car A is moving on a road with speed of 60 km/h and car B is moving with a speed of 75 km/h, along parallel straight paths, starting from the same point. What is the position of car A w.r.t. B after 20 minutes?

Solution:

Relative speed of A w.r.t. B

  60 – 75 

  – 15 km/h

Distance of A from B after 20 min

  – 15 ×  

  – 5 km.