Average Speed and Instantaneous
Velocity
Speed:
The speed of an object is the magnitude of its velocity (the rate of
change of its position); it is thus a scalar quantity. The SI unit of speed is
the metre per second.
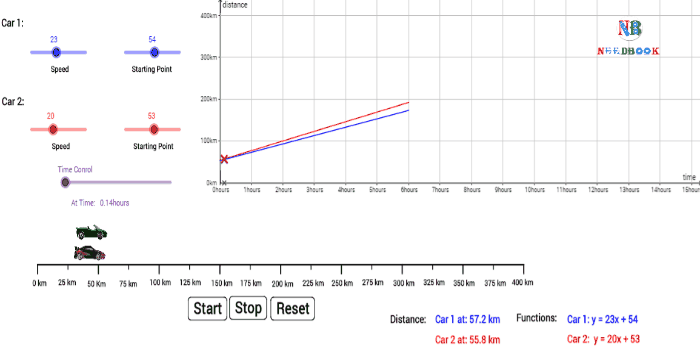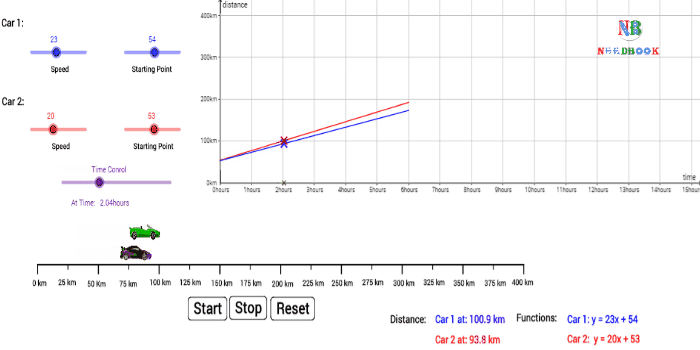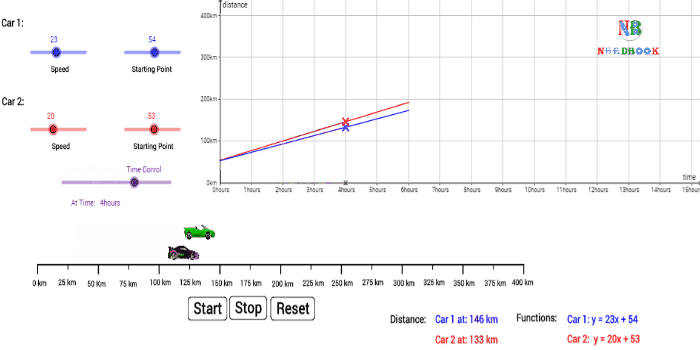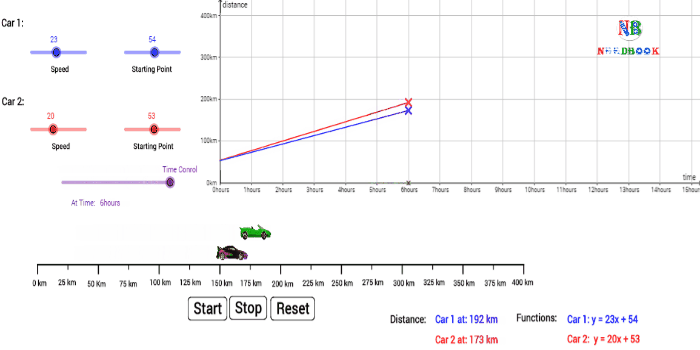
Average Speed:
Average speed is defined as the total path length travelled divided by
the total time interval during which the motion has taken place
:
Average speed 
Average speed has obviously the same unit (m s–1) as that of
velocity, but it does not tell us in what direction an object is moving. Thus,
it is always positive (in contrast to the average velocity which can be
positive or negative).
If the motion of an object is along a straight line and in the same
direction, the magnitude of displacement is equal to the total path length. In
that case, the magnitude of average velocity is equal to the average speed.
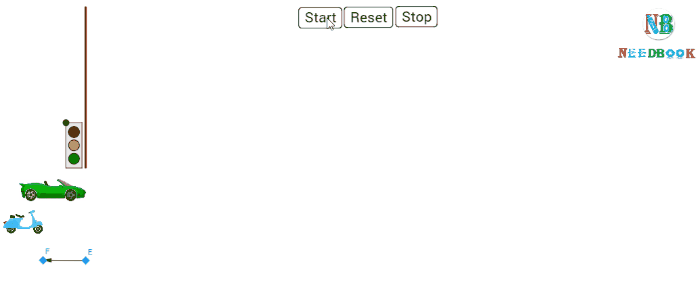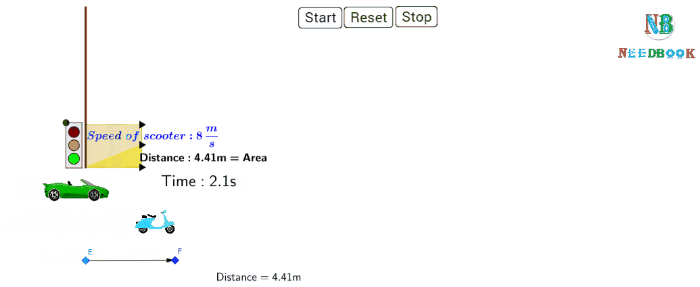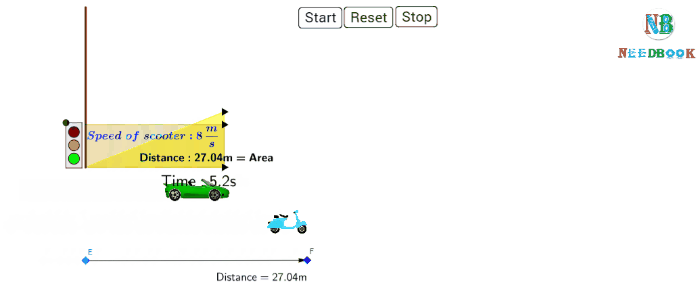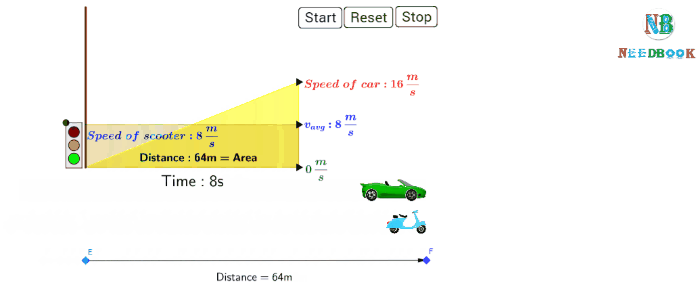
Average Velocity:
When an object is in motion, its position changes with time. But how
fast is the position changing with time and in what direction? To describe
this, we define the quantity average velocity. Average velocity is defined as
the change in position or displacement (
) divided by the time intervals (Δt), in which the
displacement occurs :
where 
and 
are the positions of the object at time t2 and t1,
respectively. Here the bar over the symbol for velocity is a standard notation
used to indicate an average quantity. The SI unit for velocity is m/s or m s–1,
although km h–1 is used in many everyday applications.
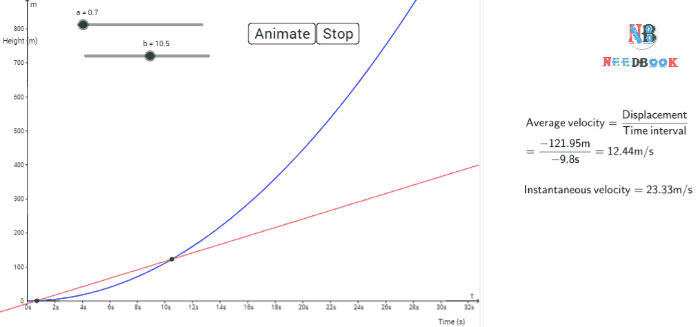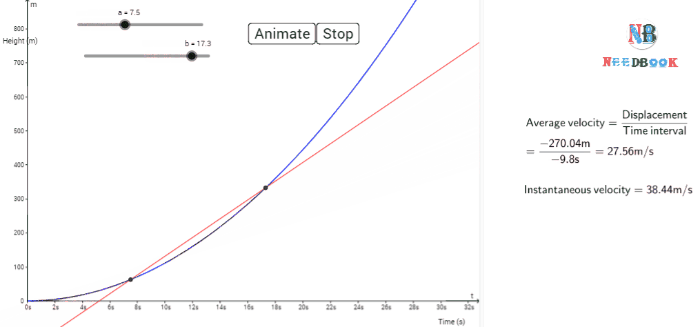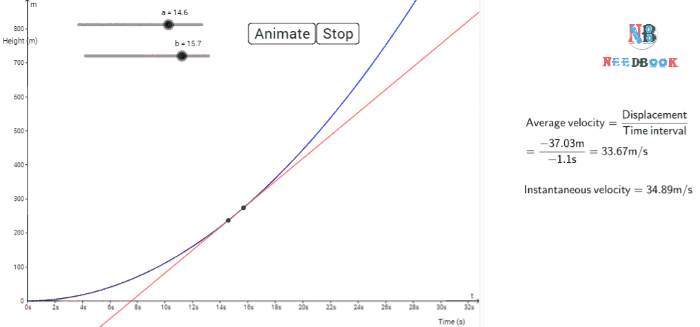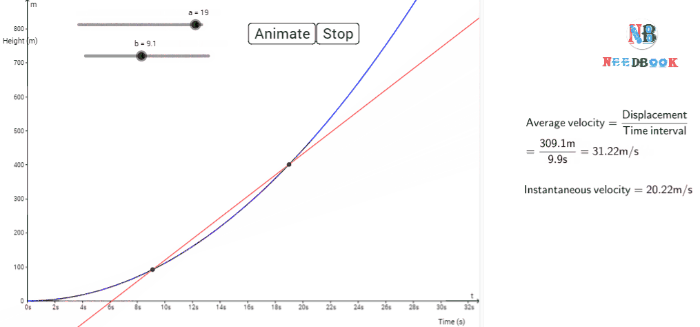
Instantaneous
Velocity:
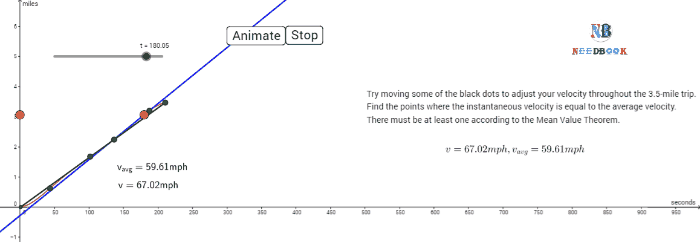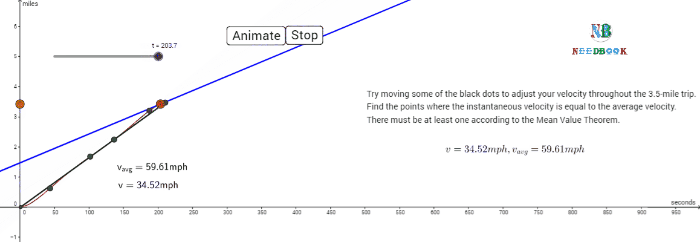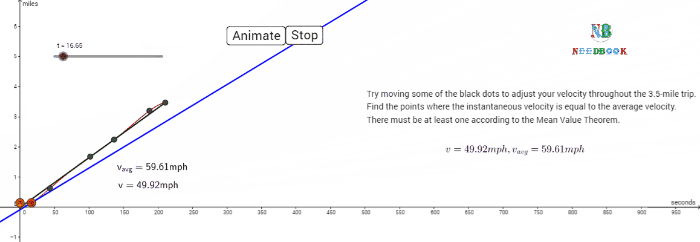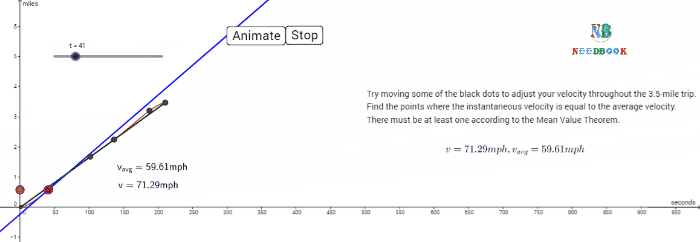
The average velocity tells us how fast an object has been moving over a
given time interval but does not tell us how fast it moves at different
instants of time during that interval. For this, we define instantaneous
velocity or simply velocity 
at an instant t.
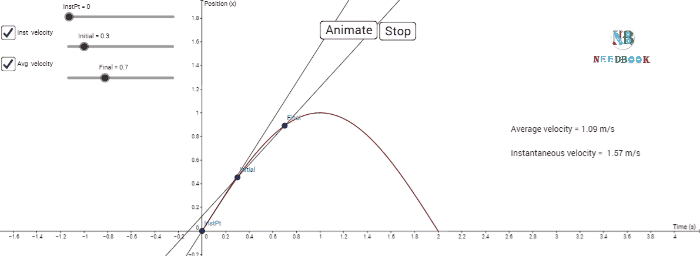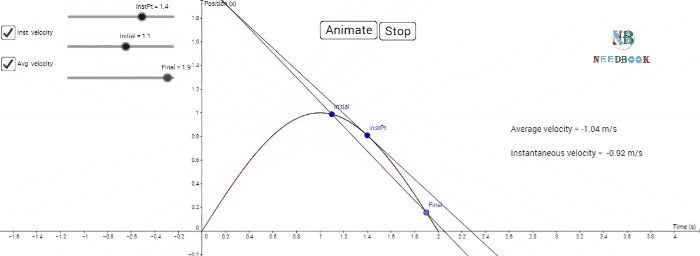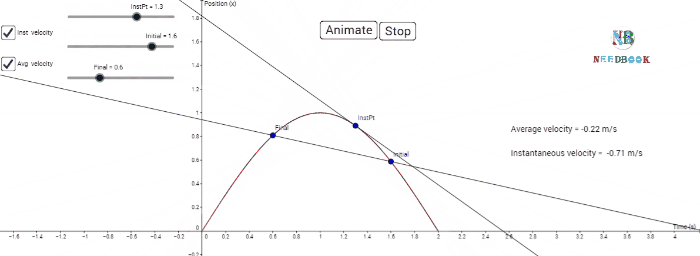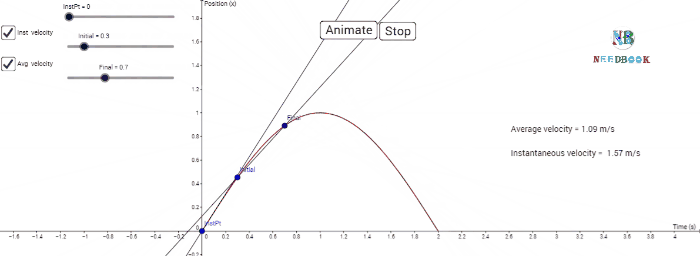
The velocity at an instant is defined as the limit of the average
velocity as the time interval Δt becomes
infinitesimally small. In other words,
------
(1a)
------
(1b)
where the symbol
stands for the operation of taking limit as Δt→0 of
the quantity on its right. In the language of calculus, the quantity on the
right hand side of eq. (1a) is the differential coefficient of 
with respect to t and is denoted by 
. It is the rate of change of position with respect to time, at that instant.
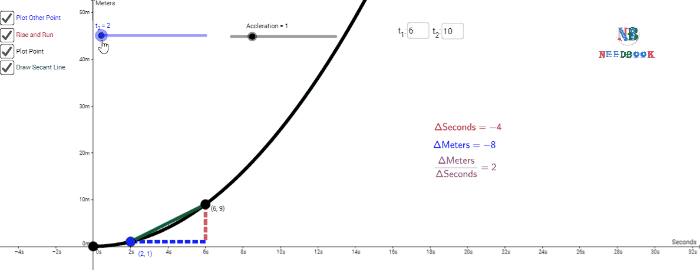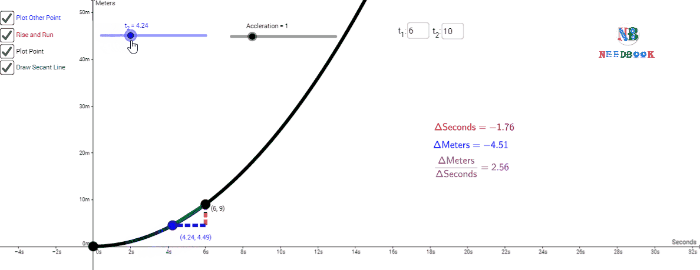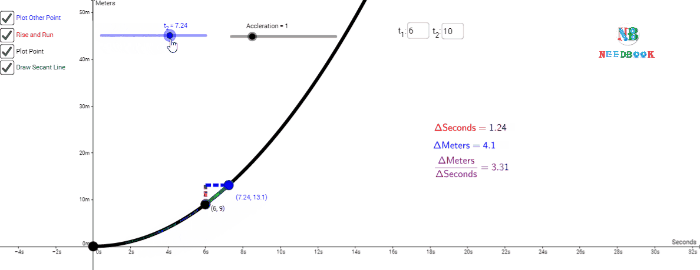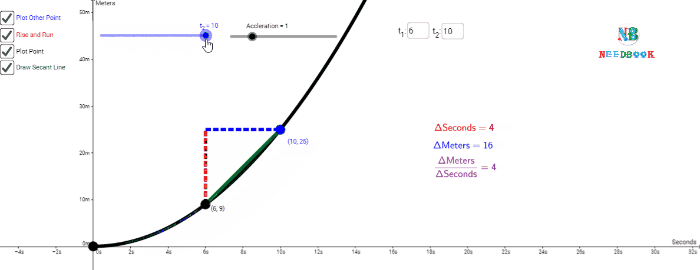
We can use Eq. (1a) for obtaining
the value of velocity at an instant either graphically or numerically. Suppose
that we want to obtain graphically the value of velocity at time t
4 s (point P) for the motion of the car represented in below figure.
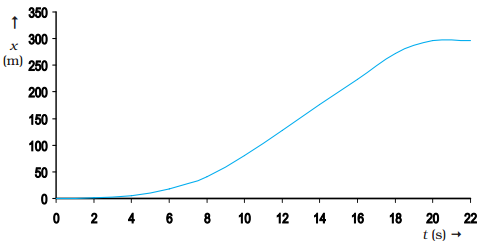
The figure has been redrawn below
choosing different scales to facilitate the calculation.
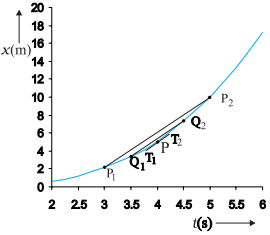
Determining velocity from position-time graph.
Velocity at t = 4 s is the slope of the tangent to the graph
at that instant.
Let us take Δt
2 s centred at t
4 s. Then, by the definition of the average velocity, the slope of line
P1P2 (above figure) gives the value of average
velocity over the interval 3 s to 5 s. Now, we decrease the value of Δt from 2 s to 1
s.
Then line P1P2 becomes
Q1Q2 and its slope gives the value of the average
velocity over the interval 3.5 s to 4.5 s. In the limit Δt→0,
the line P1P2 becomes tangent to the position-time
curve at the point P and the velocity at t
4 s is given by the slope of the tangent at that point.
It is difficult to show this
process graphically. But if we use numerical method to obtain the value of the
velocity, the meaning of the limiting process becomes clear.
For the graph shown in above
figure,
0.08 
.
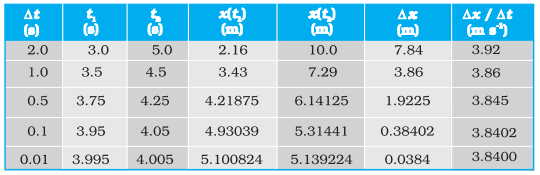
Limiting value of 
at t
4 s
Above table gives the value of calculated for Δt equal
to 2.0 s, 1.0 s, 0.5 s, 0.1 s and 0.01 s centred at t 4.0 s. The second and third columns give the
value of t1
and t2
and the fourth and the fifth columns give the
corresponding values of x, i.e. (t1)
0.08 
and (t2)
0.08 
. The sixth column lists the
difference Δ 
(t2) – (t1) and
the last column gives the ratio of Δ and Δt,
i.e. the average velocity corresponding to the value of Δt listed
in the first column.
We see from above table that as we
decrease the value of Δt from 2.0 s
to 0.010 s, the value of the average velocity approaches the limiting value
3.84 m s–1 which is the value of velocity at t
4.0 s, i.e. the value of 
at t
4.0 s. In this manner, we can calculate velocity at each instant for
motion of the car shown in below figure.
For this case, the variation of
velocity with time is found to be as shown in below figure.
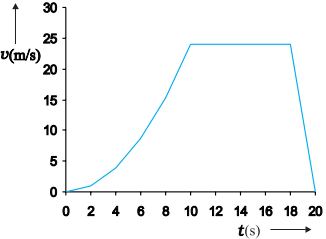
Velocity–time graph corresponding to motion (above
figure)
Problems:
1. On a 60km track, a train travels the first 30 km with a uniform speed
of 30 km/h. How fast must the train travel the next 30km so as to average 40
km/h for the entire trip?
Solution:
Time taken for first interval:
1 hr
Average speed to maintain: 40 km/hr
Total distance, s 60 km.
Since average speed 
Thus total time taken: T 
1.5 hr
Thus time taken for second interval
0.5 hr
Thus speed in second interval:
60 km/hr
2. A train moves with a speed of 30 km/h in the first 15 minutes with another
speed of 40 km/h in the next 15 minutes and then with a speed of 60 km/h in the
last 30 minutes. Calculate the average speed of the train for this journey.
Solution:
Convert all the minute units into hour.
15 minutes 
hour
hour
30 minutes 
hour
hour
Distance travelled in first 
hours 30 km/h × hours
7.5 km
Distance travelled in second hours 40 km/h × hours
10 km
Distance travelled in 
hours 60km/h × hours
30 km
Average speed
Total time taken + +
1 hour
Total distance travelled 7.5 km + 10 km + 30 km
47.5 km
Average speed 47.5 km/h
3. Three girls skating on a circular ice ground of radius 200 m start
from a point P on the edge of the ground and reach a point Q diametrically
opposite to P following different paths as shown in below figure. What is the
magnitude of the displacement vector for each?
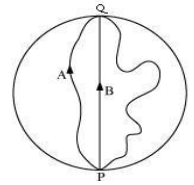
Solution:
Displacement is given by the minimum distance between the
initial and final positions of a particle. In the given case, all the girls start
from point P and reach point Q. The magnitudes of their displacements will be
equal to the diameter of the ground.
Radius of the ground 200 m
Diameter of the ground 2 × 200
400 m
4. A cyclist starts
from the centre O of a circular park of radius 1 km, reaches the edge P of the
park, then cycles along the circumference, and returns to the centre along QO
as shown in below figure. If the round trip takes 10 min, what is the average
speed of the cyclist?
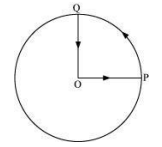
Solution:
Average speed of the cyclist is given by the relation:
Average speed 
Total path length OP + PQ + QO
1 + (2π × 1) + 1
2 + π
3.570 km
Time taken 10 min
h
∴ Average speed 
21.42 km/h
5. A passenger
arriving in a new town wishes to go from the station to a hotel located 10 km away
on a straight road from the station. A dishonest cabman takes him along a
circuitous path 23 km long and reaches the hotel in 28 min. What is the average
speed of the taxi?
Solution:
Total distance travelled 23 km
Total time taken 28 min
h
∴ Average speed of the taxi
49.29 km/h
6. A car covers the
first half of the distance between two places at a speed of 40 km/hr and second
half at 60 km/hr. Calculate the average speed of the car.
Solution:
= 40 km/hr
= 60 km/hr
Average
speed, 
= 
48 km/h
7. A cyclist moving on
a circular track of radius 100 meters completes one revolution in 4 minutes.
What is his average speed?
Solution:
Distance travelled in one revolution
2πr
2π × 100 m
Time taken 4 minute
Average time 
50π metre/minute.
|
|
|
|
