Velocity-time and Position-time
Graphs
Position-time Graphs:
Position-time Graph
for a Stationary Object:
The position of a stationary
object does not change with time. The object remains at a constant
distance 
from the origin at all times. So the position-time
graph for a stationary object is a straight
line parallel to the time-axis, as shown in below figure.
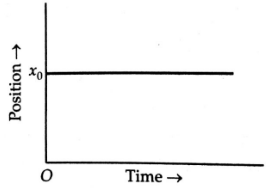
Position-time graph for a stationary object.
Position-time Graph for Uniform
Motion:
An object in uniform motion covers
equal distances in equal intervals of time. So the position-time graph for an
object in uniform motion along a straight line path is a straight line inclined
to the time-axis, as shown in below figure.
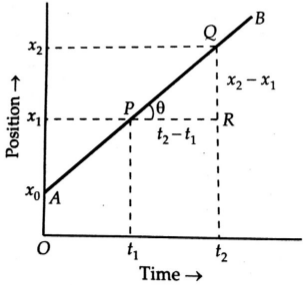
Position-time graph for a uniform motion.
Slope of position-time graph AB
tan θ
Velocity (
)
Hence the slope of the
position-time graph gives velocity of the object.
Position-time Graph for Uniformly
Accelerated Motion:
The position-time relation for
uniformly accelerated motion along a straight line is
at2
Clearly, 
i.e., is a quadratic function
of t. So the position-time graph for uniformly accelerated motion is
a parabola, as shown in below figure.
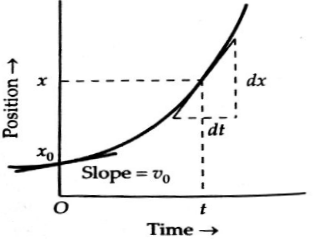
Position-time graph for a uniform acceleration.
Slope of position-time graph
velocity
at instant t
Thus the slope of the position-time graph gives the instantaneous
velocity of the object. Moreover, the slope of the 
graph at time t 0 gives the initial
velocity 
of the object.
Velocity-time Graphs:
Velocity-time Graph for Uniform Motion:
When an object has uniform motion,
it moves with uniform velocity in the same fixed direction. So the
velocity-time graph for uniform motion is a straight line parallel to the
time-axis, as shown in below figure.
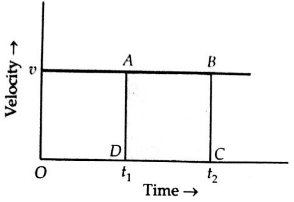
Velocity-time graph for uniform motion.
Area under the velocity-time graph
between times t1 and t2
Area of rectangle ABCD
AD × DC
(t1 − t2)
Velocity × time
Displacement
Hence the area under the
velocity-time graph gives the displacement of the object in the given time
interval.
Velocity-time Graph for Uniformly
Accelerated Motion:
When a body moves with a uniform
acceleration, its velocity changes by equal amounts in equal intervals of time.
So the velocity-time graph for a uniformly accelerated motion is a straight
line inclined to the time-axis, as shown in below figure.
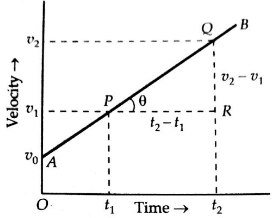
Velocity-time graph for uniform acceleration.
Slope of velocity-time graph AB
tan θ
Acceleration (a)
Hence the slope of the
velocity-time graph gives the acceleration of the object.
Distance Covered as Area Under the
Velocity-time Graph:
In below figure, the straight
line AB is the velocity-time graph of an object moving along a
straight line path with uniform acceleration a. Let its velocities
be 
and at times 0 and t respectively.
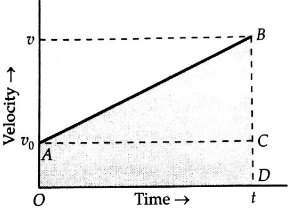
Area under velocity-time graph.
Area under the velocity-time
graph AB
Area of trapezium OABD
(OA + BD)
× OD
(+ ) × (t - 0)
Average velocity × time interval
Distance travelled in time t
Hence the area under the
velocity-time graph gives the distance travelled by the object in the given
time interval.
Equations of Motion by Graphical
Method:
Consider an object moving along a straight
line path with initial velocity u and uniform
acceleration a. Suppose it travels
distances in time t. As shown in below figure, its velocity-time
graph is straight line. Here OA ED u, OC EB and OE t AD.
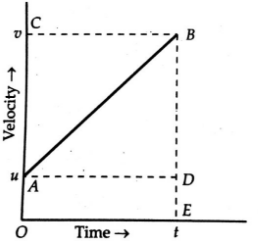
Velocity-time graph for uniform acceleration.
(i) We know that,
Acceleration
Slope of velocity-time graph AB
or,
a 
or, − u at
or,
u + at
This proves the first equation of motion.
(ii) From part (i), we have
a 
or
DB at
Distance travelled by the object in time t is
s Area of the trapezium OABE
Area of rectangle OADE +
Area of triangle ADB
OA × OE + DB × AD
ut +
at × t or s
ut +
at2
This proves the second equation of motion.
(iii) Distance travelled by object in time t is
s Area of trapezium OABE
(EB + OA)
× OE
(EB + ED)
× OE
Acceleration,
a Slope of velocity-time
graph AB
a
or OE 
∴ s
(EB + ED)
×
a (EB2 - ED2)
a (
- u2)
− u2 2as
This proves the third equation of motion.
|
|
|
|
