Problems

1. A point moves with uniform acceleration and ,  and  denote the average velocities in the three successive intervals of time , and . Which of the following relations is correct?

Solution:

Suppose u be the initial velocity

Velocity after time

Velocity after time

Velocity after time

Now,

So

() : () :

2. A rocket is fired vertically from the ground with a resultant vertical acceleration of 10 m s^–2. The fuel is finished in 1 min and it continues to move up. What is the maximum height reached?

Solution:

Height covered in 1 min,

18000 m

Velocity attained after 1 min,

0 + 10 × 60

600 m s^-1

After the fuel is finished, 600 m s^-1, 0

or

or

18367.3 m

Maximum height reached

36367.3 m ≃ 36.4 km

3. A particle moves along a straight line such that its position at any time t is = 6t² – t³ where is in m and t is in s. which of the following statements are correct?

(i) At t = 0 acceleration is 12 m s^–2

(ii) − t curve has maxima at 4 s

(iii) At t = 0 acceleration is 12 m s^–2 and − t curve has maxima at 4 s are wrong

(iv) At t = 0 acceleration is 12 m s^–2 and − t curve has maxima at 4 s are correct

Solution:

Given,

∴

For maximum or minimum

or t = 4 s

Again differentiating, we get

At t = 4 s,

−12

Since is negative, hence t 4 s gives the maxima value for -t curve.

Acceleration, , At t 0, 12 m s^-2

∴ At t = 0 acceleration is 12 m s^–2 and − t curve has maximum at 4 s are correct

4. A particle starts from rest and has an acceleration of 2 m s^–2 for 10 s. After that, the particle travels for 30 s with constant speed and then undergoes a retardation of 4 m s^–2 and comes back to rest. What is the total distance covered by the particle?

Solution:

Given, 0, 2 m s^-2, t 10 s

100 m

0 10 2

20 m s^-1

For motion with constant speed:

t 30 s

For motion with retardation:

, ,

As

Total distance covered

m

5. A parachutist jumps first freely from an aeroplane for 10 s and then his parachute opens out. Then he descends with a net retardation of 2.5 m s^–2. If he bails out of the plane at a height of 2495 m and g = 10 m s^–2, his velocity on reaching the ground will be?

Solution:

The velocity acquired by the parachutist after 10 s is

100 m s^–1

Then,

500 m

The distance travelled by the parachutist under retardation is

m

Let  be the velocity on reaching the ground. Then

or (100)²

or 5 m s^–1

6. A car A is travelling on a straight level road with a speed of 60 km h^–1. It is followed by another car B which is moving with a speed of 70 km h^–1. When the distance between them is 2.5 km, the car B is given a deceleration of 20 km h^–2. After what distance will the car B catch up with car A?

Solution:

Relative velocity of car B w.r.t. A

km h^-1

For car B,

, km, km h^-2

As

h

Actual distance travelled by car B during this time,

km

7. A body travelling with uniform acceleration crosses two points A and B with velocities 20 m s^–1 and 30 m respectively. The speed of the body at the midpoint of A and B is nearest to?

Solution:

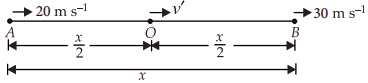
Let be the distance between two points A and B and O is the midpoint of AB. Let a be the uniform acceleration of the body and be velocity of the body at point O.

Using

According to given problem

------ (1)

And ------ (2)

Equating eqs. (1) and (2), we get

or

m s⁻¹

8. A body starts from rest and travels a distance s with uniform acceleration, then moves uniformly a distance 2 s and finally comes to rest after moving further 5 s under uniform retardation. What is the ratio of the average velocity to maximum velocity?

Solution:

Graphically, the area of –t curve represents displacement:

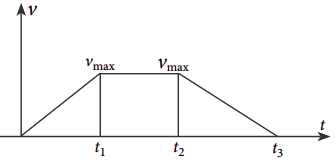
or

or

or

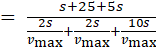
9. The velocity-displacement graph of a particle moving along a straight line is shown. What will be the most suitable acceleration-displacement graph?

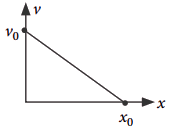
Solution:

From the given velocity-displacement graph,

Slope intercept on -axis

Thus the equation for this graph is

or

or

Clearly, the - graph must have a positive slope and negative intercept on -axis.

10. From a building two balls A and B are thrown such that A is thrown upwards and B downwards with the same speed (both vertically). If and  are their respective velocities on reaching the ground then, which of the following statements are correct?

(i)  >

(ii) Their velocities depend on their masses

(iii)  =

(iv)  >

Solution:

Let the ball A is thrown vertically upwards with speed and ball B is thrown vertically downwards with the same speed . After reaching the highest point, A comes back to its point of projection with the same speed in the downward direction.

If be height of the building, then velocity of A on reaching the ground is

or ------ (1)

And that of B on reaching the ground is

or ------ (2)

From eqs. (1) and (2), we get

is the correct statement.

11. A man runs at a speed of 4.0 m s^–1 to overtake a standing bus. When he is 6.0 m behind the door of the bus (at  t = 0), the bus moves forward and continues with a constant acceleration of 1.2 m s^–2. How long does it take for the man to gain the door?

Solution:

At t 0, let the man’s position be the origin

The bus door is then at m

Here, , m s^-1,

------ (1)

The equation for motion for the bus is

Here, m, , m s^-2

------ (2)

When the man catches the bus,

Using eqn. (1) and (2)

or

;

12. A train 100 m long travelling at 40 m s^–1 starts overtaking another train 200 m long travelling at 30 m s^–1. What is the time taken by the train to pass the second train completely?

Solution:

Relative velocity of overtaking 40 – 30

10 m s^–1

Total relative distance covered with this relative velocity during overtaking

100 + 200

300 m.

So time taken

30 s.

13. A jet airplane travelling at the speed of 500 km h^–1 ejects its products of combustion at the speed of 1500 km h^–1 relative to the jet plane. What is the speed of the latter with respect to an observer on ground?

Solution:

Speed of the jet airplane,   500 km/h

Relative speed of its products of combustion with respect to the plane,

1500 km/h

Speed of its products of combustion with respect to the ground

Relative speed of its products of combustion with respect to the airplane,

– 1500

1000 km/h

The negative sign indicates that the direction of its products of combustion is opposite to the direction of motion of the jet airplane.

14. Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h^–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m s^-2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?

Solution:

For train A:

Initial velocity, 72 km/h

20 m/s

Time, 50 s

Acceleration, 0 (Since it is moving with a uniform velocity)

From second equation of motion, distance () covered by train A can be obtained as:

1000 m

For train B:

Initial velocity, 72 km/h

20 m/s

Acceleration, 1 m s^-2

Time, 50 s

From second equation of motion, distance () covered by train A can be obtained as:

m

Hence, the original distance between the driver of train A and the guard of train B

2250 – 1000

1250 m.

15. On a two-lane road, car A is travelling with a speed of 36 km . Two cars B and C approach car A in opposite directions with a speed of 54 km h^–1 each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident?

Solution:

Velocity of car A,  km/h

10 m/s

Velocity of car B,  54 km/h

15 m/s

Velocity of car C,  54 km/h

15 m/s

Relative velocity of car B with respect to car A,

15 – 10

5 m/s

Relative velocity of car with respect to car A,

15 + 10

25 m/s

At a certain instance, both cars B and C are at the same distance from car A i.e.,

1000 m

Time taken (t) by car C to cover 1000 m

s

Hence, to avoid an accident, car B must cover the same distance in a maximum of 40 s.

From second equation of motion, minimum acceleration (a) produced by car B can be obtained as:

1 m/s²

16. A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?

Solution:

Initial velocity of the ball, 49 m/s

Acceleration, – g

– 9.8 m/s²

When the lift was stationary, the boy throws the ball.

Taking upward motion of the ball,

Final velocity, of the ball becomes zero at the highest point.

From first equation of motion, time of ascent (t) is given as:

s

But, the time of ascent is equal to the time of descent.

Hence, the total time taken by the ball to return to the boy’s hand

5 + 5

10 s.