Uniform Circular Motion

When an object follows a circular path at a constant speed, the motion of the object is called uniform circular motion. The word “uniform” refers to the speed, which is uniform (constant) throughout the motion.

Suppose an object is moving with uniform speed  in a circle of radius R as shown in below figure.

Since the velocity of the object is changing continuously in direction, the object undergoes acceleration. Let us find the magnitude and the direction of this acceleration.

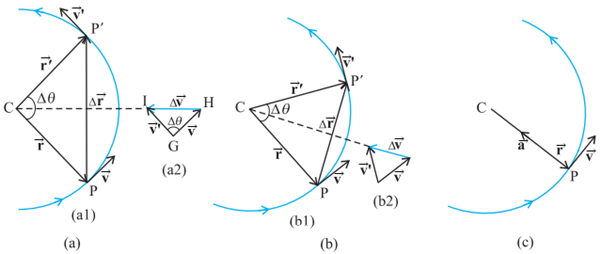
Velocity and acceleration of an object in uniform circular motion. The time interval Δt decreases from (a) to (c) where it is zero. The acceleration is directed, at each point of the path, towards the centre of the circle

Let  and  be the position vectors and  and  the velocities of the object when it is at point P and P′ as shown in above figure (a).

By definition, velocity at a point is along the tangent at that point in the direction of motion. The velocity vectors  and  are as shown in above figure (a1). Δ is obtained in figure (a2) using the triangle law of vector addition. Since the path is circular,  is perpendicular to  and so is  to . Therefore, Δ is perpendicular to Δ.

Since average acceleration is along Δ , the average acceleration  is perpendicular to Δ. If we place Δ on the line that bisects the angle between  and , we see that it is directed towards the centre of the circle. Figure (b) shows the same quantities for smaller time interval. Δ and hence  is again directed towards the centre.

In Figure (c), Δt → 0 and the average acceleration becomes the instantaneous acceleration. It is directed towards the centre. Thus, we find that the acceleration of an object in uniform circular motion is always directed towards the centre of the circle. Let us now find the magnitude of the acceleration.

The magnitude of  is, by definition, given by

Let the angle between position vectors  and  be Δθ. Since the velocity vectors  and  are always perpendicular to the position vectors, the angle between them is also Δθ. Therefore, the triangle CPP′ formed by the position vectors and the triangle GHI formed by the velocity vectors ,  and Δ are similar (figure a).

Therefore, the ratio of the base-length to side-length for one of the triangles is equal to that of the other triangle. That is :

or,

Therefore,

If Δt is small, Δθ will also be small and then arc PP′ can be approximately taken to be :

or,

Therefore, the centripetal acceleration a_c is :

------ (1)

Thus, the acceleration of an object moving with speed  in a circle of radius R has a magnitude  and is always directed towards the centre. This is why this acceleration is called centripetal acceleration (a term proposed by Newton).

A thorough analysis of centripetal acceleration was first published in 1673 by the Dutch scientist Christiaan Huygens (1629-1695) but it was probably known to Newton also some years earlier.

“Centripetal” comes from a Greek term which means ‘centre-seeking’. Since and R are constant, the magnitude of the centripetal acceleration is also constant. However, the direction changes — pointing always towards the centre. Therefore, a centripetal acceleration is not a constant vector.

We have another way of describing the velocity and the acceleration of an object in uniform circular motion. As the object moves from P to P′ in time Δt (= t′ – t), the line CP (above figure) turns through an angle Δθ as shown in the figure. Δθ is called angular distance. We define the angular speed ω (Greek letter omega) as the time rate of change of angular displacement :

ω ------ (2)

Now, if the distance travelled by the object during the time Δt is Δs, i.e. PP′ is Δs, then :

but Δs R Δθ. Therefore :

R ω ------ (3)

We can express centripetal acceleration a_c in terms of angular speed :

a_c ω²R ------ (4)

The time taken by an object to make one revolution is known as its time period T and the number of revolution made in one second is called its frequency ν . However, during this time the distance moved by the object is s 2πR.

Therefore,

2πRν ------ (5)

In terms of frequency ν, we have

ω 2πν

2πRν

a_c 4π² ν²R ------ (6)

Problems:

1. Calculate the angular speed of flywheel making 420 revolutions per minute.

Solution:

Here ν 420 revolutions/min

revolutions/s

ω 2πν

2 × ×

44 rad/s

2. Find the magnitude of the centripetal acceleration of a particle on the tip of a fan blade, 0.30 meter in diameter, rotating at 1200 rev/minute.

Solution:

Here ν

20 rps

ω 2πν

2π × 20

40 rad/s

a_c rω²

0.15 × (40π)²

2368.8 m/s

3. A circular wheel of 0.50 m radius is moving with a speed 10 m/s. Find its angular speed.

Solution:

Here r 0.50 m, ν 10 m/s

As ν rω

∴ ω

20.0 rad/s

4. Assuming that the moon completes one revolution in a circular orbit around the earth in 27.3 days, calculate the acceleration of the moon towards the earth. The radius of the circular orbit can be taken as 3.85 × 10⁵ km. 

Solution:

a rω²

r

3.85 × 10⁸ ×

2.73 × 10^-3 ms^-2

5, A thread rod with 12 turns per cm and diameter 1.18 cm is mounted horizontally. A bar with a threaded hole to match the rod is screwed onto the rod. The bar spins at the rate of 216 rpm. How long will it take for the bar to move 1.50 cm along rod?

Solution:

Pitch of threaded screw

cm

Number of rotations required to move a distance of 1.5 cm,

n

1.5/(1/12)

18

∴ θ 2π

2π × 18

36 π rad

Angular speed of the bar,

ω 2πν

2π ×

7.2 π rad s^-1

∴ Required time,

t

5 s.