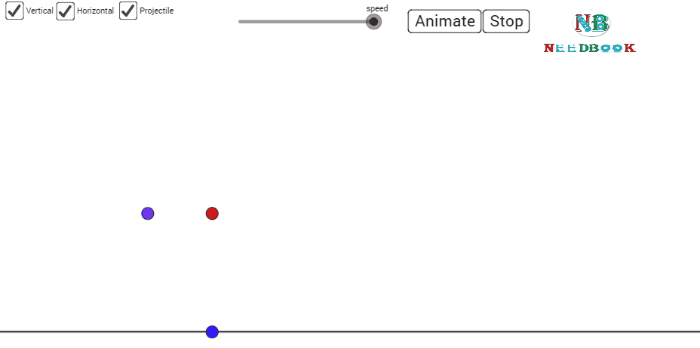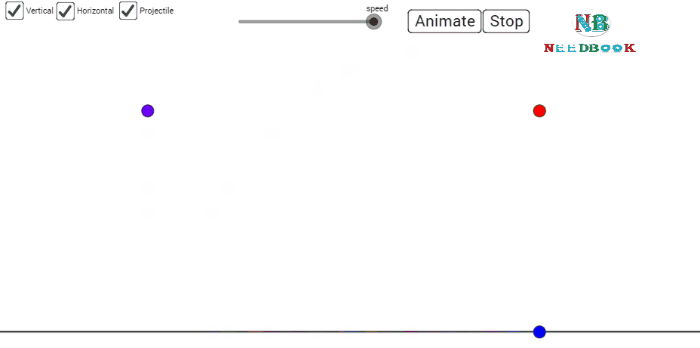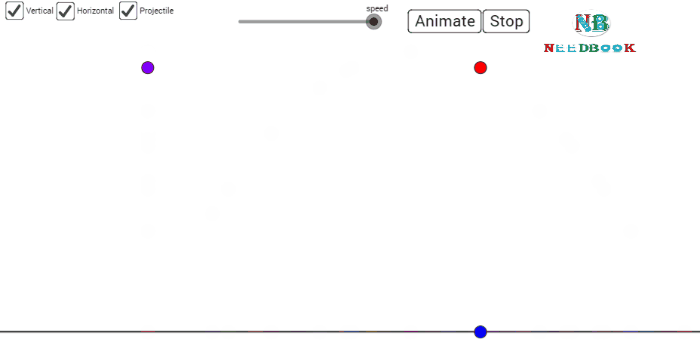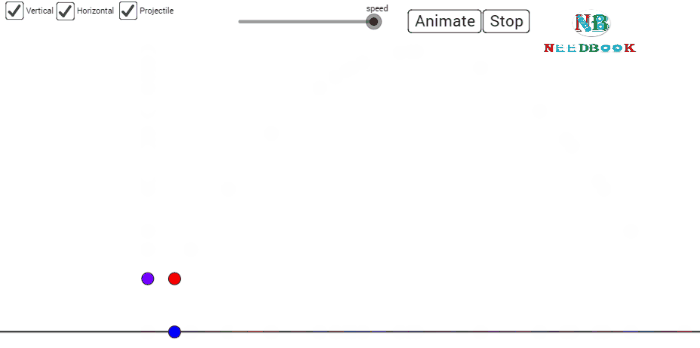
Projectile Motion

An object that is in flight after being thrown or projected is called a projectile. Such a projectile might be a football, a cricket ball, a baseball or any other object. 

The motion of a projectile may be thought of as the result of two separate, simultaneously occurring components of motions. One component is along a horizontal direction without any acceleration and the other along the vertical direction with constant acceleration due to the force of gravity. It was Galileo who first stated this independency of the horizontal and the vertical components of projectile motion in his Dialogue on the great world systems (1632).

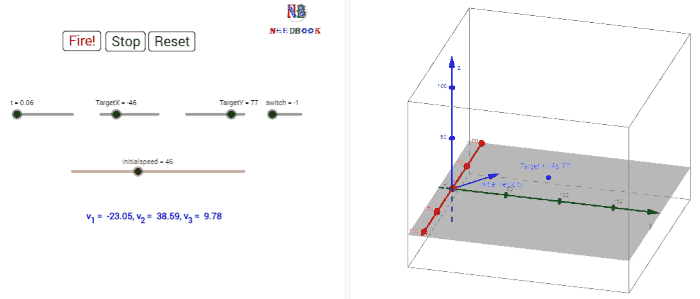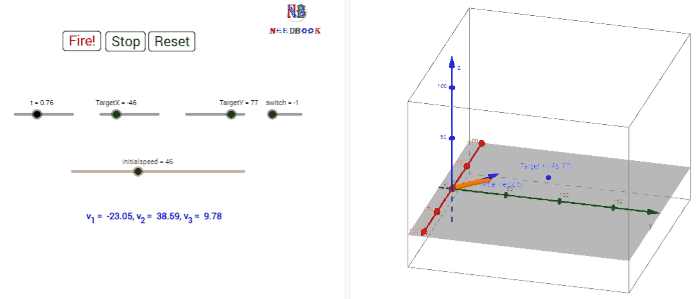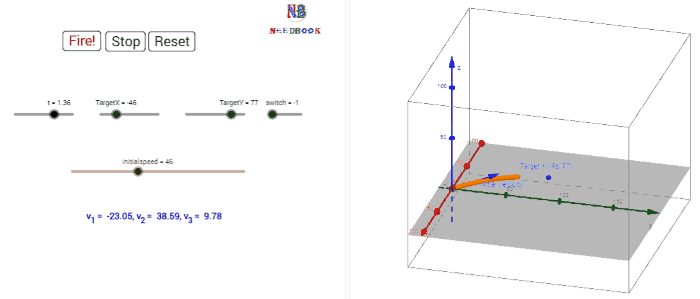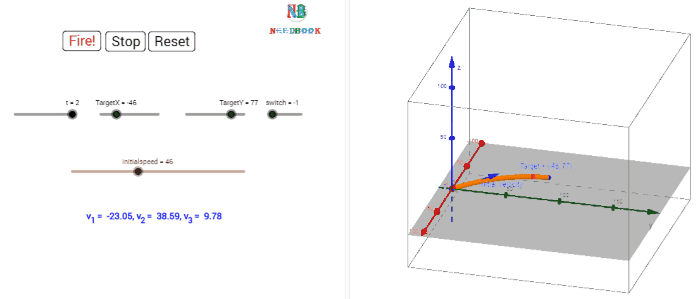
In our discussion, we shall assume that the air resistance has negligible effect on the motion of the projectile. Suppose that the projectile is launched with velocity  that makes an angle θ0 with the -axis as shown in below figure.

After the object has been projected, the acceleration acting on it is that due to gravity which is directed vertically downward:

   −g 

or,                                                     ------ (1)

The components of initial velocity   are :

 

                                                    ------ (2)

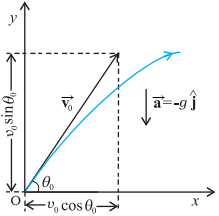
Motion of an object projected with velocity  at angle .

If we take the initial position to be the origin of the reference frame as shown in above figure, we have :

            

   

       

and                                      ------ (3)

The components of velocity at time t can be obtained using (Eq. 9b - Motion in a plane: ):

            

          

                                          ------ (4)

Equation (3) gives the , and -coordinates of the position of a projectile at time t in terms of two parameters — initial speed  and projection angle θ0. Notice that the choice of mutually perpendicular -, and -directions for the analysis of the projectile motion has resulted in a simplification. 

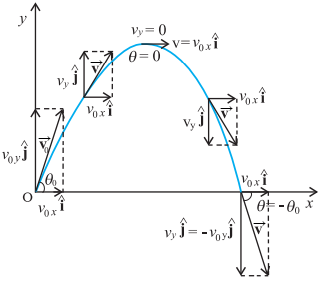
One of the components of velocity, i.e. -component remains constant throughout the motion and only the - component changes, like an object in free fall in vertical direction. This is shown graphically at few instants in below figure. Note that at the point of maximum height,     0 and therefore,

  

       

Equation of path of a projectile:

What is the shape of the path followed by the projectile? This can be seen by eliminating the time between the expressions for  and  as given in Eq. (3). We obtain:

               --- (5)

Now, since g, θ0 and  are constants, Eq. (5) is of the form  in which  and  are constants. This is the equation of a parabola, i.e. the path of the projectile is a parabola (below figure).

The path of a projectile is a parabola

Time of maximum height:

How much time does the projectile take to reach the maximum height ? Let this time be denoted by tm. Since at this point,     0, we have from Eq. (4):

           

      

or,                 =                                               ------ (6a)

The total time Tf during which the projectile is in flight can be obtained by putting  = 0 in Eq. (4). We get :

           Tf                                           ------ (6b)

Tf is known as the time of flight of the projectile. We note that Tf     2 tm, which is expected because of the symmetry of the parabolic path.

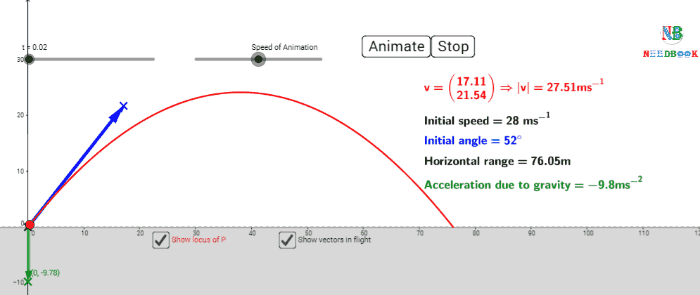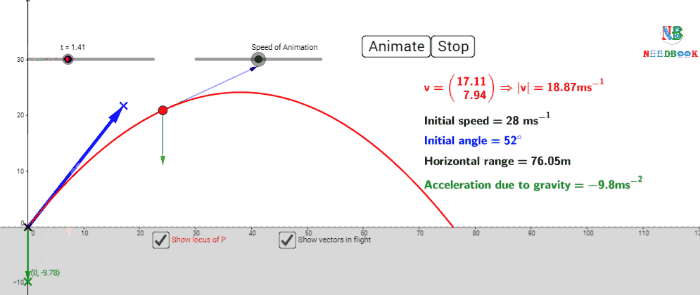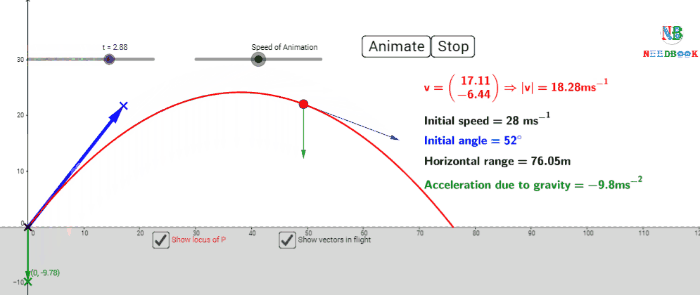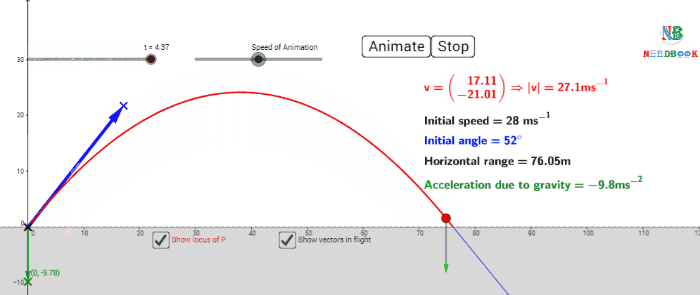
Maximum height of a projectile:

The maximum height  reached by the projectile can be calculated by substituting t = tm in Eq. (4) :

 

      

or,                                                              ------ (7)

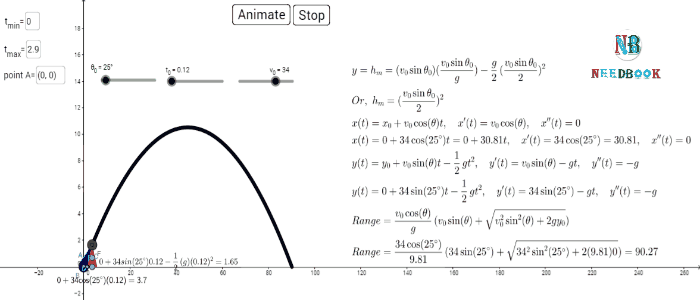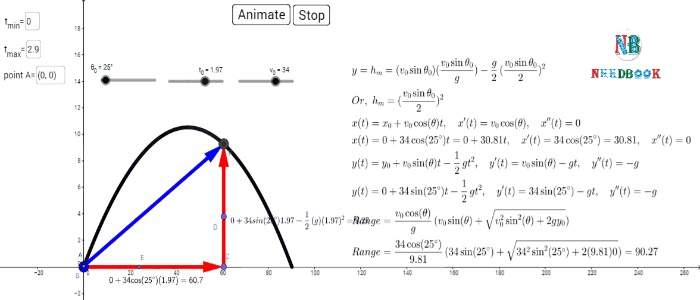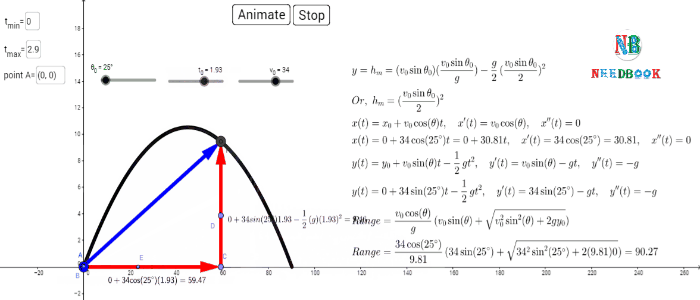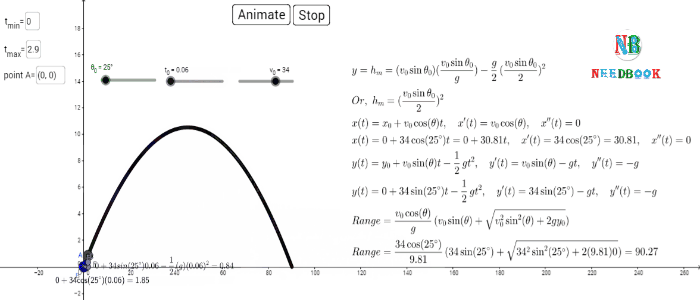
Horizontal range of a projectile:

The horizontal distance travelled by a projectile from its initial position () to the position where it passes   0 during its fall is called the horizontal range, R. It is the distance travelled during the time of flight Tf. Therefore, the range R is

 

      

or,                                                                ------ (8a)

Equation (8a) shows that for a given projection velocity v0, R is maximum when sin 2θ0 is maximum, i.e., when θ0    45°.

The maximum horizontal range is, therefore,

                                                                    ------ (8b)

Problems:

1. A bomb is dropped from an aeroplane when it is directly above a target at a height of 1000 m. The aeroplane is moving horizontally with a speed of 500 km/h. By how much distance will the bomb miss the target?

Solution:

As the aeroplane is moving horizontally, the initial downward velocity of the bomb, .

Also                  m,  ms-2, t    ?

Now                

∴                

or                      

      

Horizontal velocity of the aeroplane 

       500 km/h

        m/s

      m/s

Distance by which the bomb misses the target

       Horizontal distance covered by the bomb before it hits the ground

       Horizontal velocity  time

      

       1984.13 m.

 

2. A marksman wishes to hit a target just in the same level as the line of sight. How high from the target he should aim, if the distance of the target is 1600 m and the muzzle velocity of the gun is 800 m/s. (Take g    9.8 ms−2)

Solution:

Let u be the speed of the bullet.

In time t, it covers a horizontal distance,

   1600 m

But     

∴       or      2 s

Distance through which the bullet is pulled down by the force of gravity in 2 s is

 

      

     19.6 m.

 

3. Two tall buildings face each other and are at a distance of 180 m from each other. With what velocity must a ball be thrown horizontally from a window 55 m above the ground in one building, so that enters a window 10.9 m above the ground in the second building?

Solution:

Vertical downward distance to be covered by the ball

  Height of W1 − Height of W2

  55 − 10.9

  44.1 m

Initial vertical velocity of ball,

      

As                                                  

∴                                              

or                                                     

   9

or                                                     3 s

Required horizontal velocity  

 

 60 m/s

 

4. A mail bag is to be dropped into a post office from an aeroplane flying horizontally with a velocity 270 km/h at a height 176.4 m above the ground. How far must the aeroplane be from the post office at the time of dropping the bag so that it directly falls into the post office?

Solution:

For vertical motion:

  

∴             

or                   

     36

∴                       6 s

Also                 270 km/h

    =  

       75 m/s

∴                     

      

       450 m.

 

5. A projectile has a range of 50 m and reaches a maximum height of 10 m. Calculate the angle at which the projectile is fired. 

Solution:

Here                 50 m,   10,   ?

Horizontal range,

  

    =                      ------ (1)

Maximum height,

                                ------ (2)

Dividing (2) by (1), we get

 

     =  tan θ

or            tan θ   

    =   

       0.8

or                     tan-1(0.8)

       38.66°

 

6. Find the angle of projection for which the horizontal range and the maximum height are equal.

Solution:

Horizontal range    Maximum height

or              =   

or     2 sin θ cos θ    sin2 

                      =  4

or                  tan θ    4

       75°58′

 

7. A ball is kicked at an angle of 30° with the vertical. If the horizontal component of its velocity is 19.6 m/s, find the maximum height.

Solution:

Here                         

     

Horizontal velocity     cos 60°

    19.6 m/s

∴                                  

    =   

      39.2 m/s

∴ Maximum height,

           

    

      58.8 m

Horizontal range,

             

    

    

     135.8 m

 

8. A machine gun is mounted on the top of a tower 100 m high. At what angle should the gun be inclined to cover a maximum range of firing on the ground below? The muzzle speed of bullet is 150 m/s. Take g    10 ms−2.

Solution:

Let  be the muzzle speed of bullet fired from the gun (on the top of a tower) at an angle θ with the horizontal.

Clearly, the total range of firing on the ground is

 

∴                                                        =   

     

      

For  to be max.,

          

or    

or          90 sin4 θ45 sin2 θ + 1  0

or                                              sin2 θ 

     

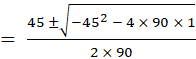
Taking only positive sign,

   sin2 θ    0.4767

or                                               sin θ    0.6904

or                                                      θ    43.7°