Escape Velocity
Escape Velocity:
If we throw a ball into air, it rises
to a certain height and falls back. If we throw it with a greater velocity, it
rises to a greater height. If we throw it with a sufficient velocity, it will never
come back. It will escape from the gravitational pull of the earth. This
minimum velocity is called escape velocity.
Escape
velocity is the minimum velocity with which a body must be projected vertically
upwards in order that it may just escape the gravitational field of the earth.
Expression
for Escape Velocity:
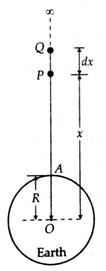
Consider the earth to be a sphere of mass M and radius R with centre O. Suppose
a body of mass m lies at point P at distance 
from its centre,
as shown in below figure.
The
gravitational force of attraction on the body at P is
F = 
The small work done in moving the body through small distance 
against the gravitational force is given by
dW = 
= 
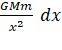
The total work done in moving the body from the surface of the
earth 
to a region beyond the gravitational field of
the earth 
will be
W = 
= 
= 
= 
= 
= 
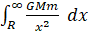
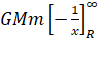
If 
is the escape velocity of the body, then the
kinetic energy 
imparted to the body at the surface of the earth will be just sufficient to perform
work W
∴
= 
= 
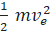Escape velocity
= 
------
(i)
As g
= 
or
GM = 
∴ = 
or
= 
------ (ii)
If 
is the mean density of the earth, then
M =
∴ = 
= 
------
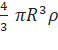
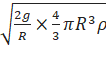
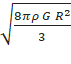(iii)
Equations (i), (ii) and (iii) give
different expressions for the escape velocity of a body. Clearly, the escape
velocity does not depend on the mass of the body projected.
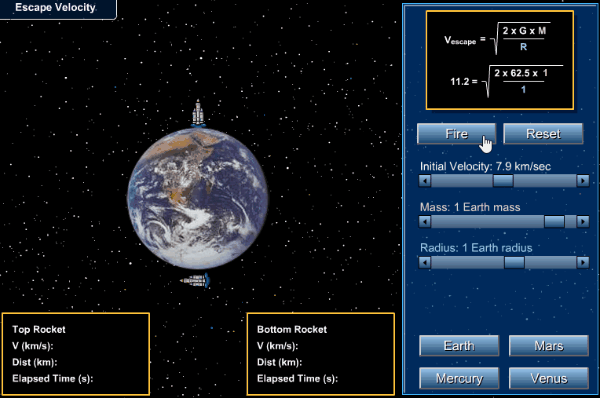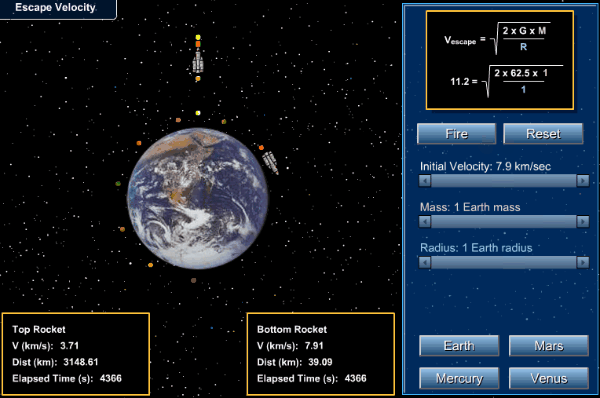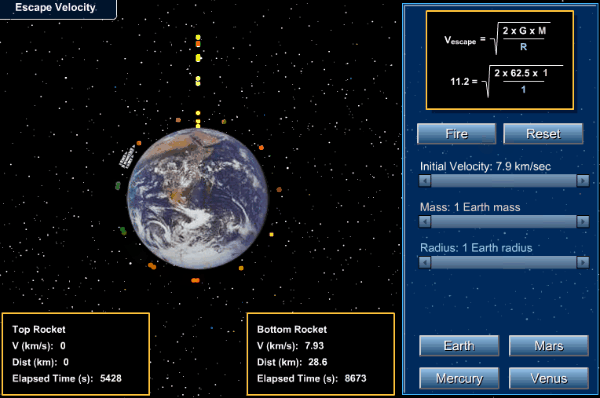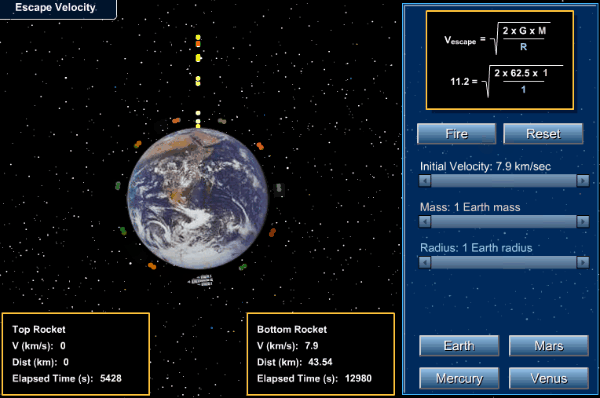
Problems:
1. Find the velocity of escape at the earth given
that its radius is 6.4 × 106 m and the
value of g at its surface is 9.8 ms-2.
Solution:
Here R = 6.4 × 106 m, g = 9.8 ms−2
= 
= 
= 11.2 × 103
ms−1
= 11.2 kms−1
2.
Determine the escape velocity of a body from the moon. Take the moon to be a
uniform sphere of radius 1.76 × 106 m, mass 7.36 × 1022
kg.
Solution:
Given
G = 6.67 × 10−11
Nm−2 kg−2
M = 7.36 × 1022 kg
=
= 
= 2375 ms−1
= 2.375 km s−1
3.
A black hole is a body from whose surface nothing may even escape. What is the
condition for a uniform spherical body of mass M to be a black hole if its mass is nine times the mass of the
earth?
Solution:
From
Einstein’s special theory of relativity, we know that light speed of any object
cannot exceed the speed of light, c = 3 × 108 ms−1.
Thus c is the upper limit to the projectile’s escape velocity. Hence for a body
to be a black hole,
= 
If M = 9 ME = 9× 6 ×1024
kg, then
R = 
=
= 8 × 10−2 m or nearly 8 cm
4.
Jupiter has a mass 318 times that of the earth, and its radius is 11.2 times
the earth’s radius. Estimate the escape velocity of a body from Jupiter’s
surface, given that the escape velocity from the earth surface is 11.2 km s−1.
Solution:
Escape
velocity from the earth surface is
= 
=
11.2 km s−1
Escape velocity of a body from Jupiter’s
surface will be
= 
But M’ = 318 M, R’
= 11.2 R
= 
=
= 
= 59.7 kms-1
5.
Show that the moon would depart for ever if its speed were increased by 42%.
Solution:
The centripetal force required by
the moon to revolve around the earth is provided by gravitational attraction.
∴
= 
= 
=
= 
Velocity required to escape,
= 
% increase in the velocity of moon
= 
× 100
= 
× 100
= 
× 100
= (1.414 -1) × 100
= 41.4 % 
42%
6.
Calculate the escape velocity for an atmospheric particle 1600 km above the
earth surface, given that the radius of the earth is 6400 km and acceleration
due to gravity on the surface of earth is 9.8 ms−2.
Solution:
At
a height h above the earth’s surface, we have
= 
,
= 
∴ = 
= 
But g = 9.8 ms−2, R = 6.4 × 106 m
h = 1600 km
= 1.6 × 106 m
R +
h = (6.4 + 1.6) × 106
= 8 × 106 m
= 
= 10.02 × 103
ms−1
= 10.02 kms−1
7. A body
is at height equal to the radius of the earth from the surface of the earth.
With what velocity thrown so that it goes out of the gravitational field of the
earth? Given Me
= 6.0 × 1024 kg, Re
= 6.4 106 m and G = 6.67 ×
10−11 Nm−2 kg−2.
Solution:
Escape from the earth’s surface
= 
If
the body is at height Re from the earth surface. Then the distance of the
body from the centre of earth will be 2Re. Hence in this case, the
escape velocity of the body will be
=
= 
= 7.9 × 103 ms−1
= 7.9 kms−1
8. A body
of mass 100 kg falls on the earth from infinity. What will be its velocity on
reaching the earth? What will be its K.E.? Radius of the earth is 6400 km and g = 9.8 ms−2. Air
friction is negligible.
Solution:
A body thrown up with escape velocity reaches infinity.Hence a body falling on the
earth from infinity should come back with velocity given by
= 
=
= 11.2 × 103 ms-1
= 11.2 kms-1
K.E. = 
= 
× 100 × (11.2 × 103)2
= 6.27 × 109 J
|
|
|
|
