Orbital Velocity

Orbital Velocity: Orbital velocity is that velocity required to put the satellite into its orbit around the earth.

Expression for Orbital Velocity:

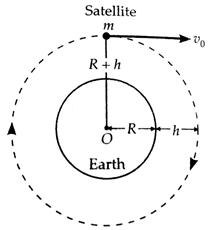
Let

M = mass of the earth,

R = radius of the earth,

m = mass of the satellite,

= orbital velocity of the satellite

h = height of the satellite above the earth surface

R + h = orbital radius of the satellite,

According to the law of gravitation the force of the gravity on the satellite is

F =

The centripetal force required by the satellite to keep it in its orbit is

F =

In equilibrium, the centripetal force is just provided by the gravitational pull of the earth, so

=

=

∴ Orbital velocity,

= ------ (i)

If g is the acceleration due to gravity on the earth surface then

g =

GM =

Hence

=

=

When the satellite revolves close to the surface of the earth h = 0 and orbital velocity will become

=

As g = 9.8 ms⁻² and R = 6.4 × 10⁶ m, so

=

= 7.92 × 10³ ms⁻¹

= 7.92 kms⁻¹

Relation between Orbital Velocity and Escape Velocity:

The escape velocity of a body from the earth’s surface is

=

The orbital velocity of a satellite revolving close to the earth’s surface is

=

∴ =

=

or =

Hence the escape velocity of a body from the earth’s surface is times its velocity in a circular orbit just above the earth’s surface.

Problems:

1. The orbit of a geostationary satellite is concentric and coplanar with the equator of earth and rotates along the direction of rotation of earth. Calculate the height and speed. Take mass of earth = 5.98 × 10²⁷ g and its radius = 6400 km. given = 9.87.

Solution:

Here T = 24 × 3600 s,

G = 6.67 × 10⁻¹¹ Nm²kg⁻²

M = 5.98 × 10²⁷

g = 5.98 × 10²⁴ kg

R = 6400 km

R + h =

=

= 4.225 × 10⁷ m

= 42250 km

∴ h = 42250 − 6400

= 35850 km

Orbital speed,

=

=

= 3.071 kms⁻¹

2. An artificial satellite of mass 100 kg is in a circular orbit of 500 km above the earth surface. Take radius of earth as 6.5 × 10⁶ m. (i) Find the acceleration due to gravity at any point along the satellite path. (ii) What is the centripetal acceleration of satellite? Take g = 9.8 ms⁻²

Solution:

Here h = 500 km

= 0.5 × 10⁶ m

R = 6.5 × 10⁶ m

∴ R + h = 7.0 × 10⁶ m

(i) g’ = g

= 9.8

= 8.45 ms⁻²

(ii) a_c =

= ×

= 8.45 ms⁻²

3. A space ship is launched into a circular orbit close to the earth’s surface. What additional velocity has now to be imparted to the space ship in the orbit to overcome the gravitational pull? (Radius of the earth = 6400 km, g = 9.8 ms⁻²).

Solution:

Orbital velocity near the earth surface,

=

Escape velocity,

=

=

Additional velocity required

=

=

= 0.414 ×

= 3.278 × 10³ ms⁻¹

=3.278 kms⁻¹

4. An artificial satellite revolves around the earth at a height of 1000km.The radius of the earth is 6.38 × 10³ km. Mass of the earth is 6 × 10²⁴ kg and G = 6.67 × 10⁻¹¹ Nm² kg⁻². Find its orbital velocity and period of revolution.

Solution:

Here

h = 1000 km

= 10⁶ m

R = 6.38 × 10³ km

= 6.38 × 10⁶ m

∴ R + h = 7.38 × 10⁶ m,

M = 6 × 10²⁴ kg

Orbital velocity

=

=

= 7364 ms⁻¹

Period of revolution,

T =

=

= 6297 s

5. An remote sensing satellite of the earth revolves in a circular orbit at a height of 250 km above the earth’s surface. What is the (i) orbital speed and (ii) period of revolution of the satellite? Radius of the earth, R = 6.38 × 10⁶ m, and acceleration due to gravity on the surface of the earth, g = 9.8 ms⁻².

Solution:

(i) Here g = 9.8 ms⁻², R = 6.38 × 10⁶ m, h = 250,000 m

R + h = 6.38 × 10⁶ + 250,000

= 6.63 × 10⁶ m

The orbital speed is given by

=

=

= 7.76 × 10³ ms⁻¹

= 7.76 kms⁻¹

(ii) The period of revolution of the satellite will be

T =

=

= 5370 s

6. An artificial satellite is going round the earth, close to its surface. What is the time taken by it to complete one round? Given radius of earth = 6400 km.

Solution:

Here

R = 6400 km = 6.4 × 10⁶ m,

g = 9.8 ms^-2

Orbital velocity near the earth surface is

=

=

= 7290 ms^-1

Time period,

T =

=

= 5079 s

= 1.411 hour

7. A satellite revolves in an orbit close to the surface of a planet of mean density 5.51 × 10³ kg m⁻³. Calculate the time period of satellite. Given G = 6.67 × 10⁻¹¹

Solution:

Here = 5.51 × 10³ kgm⁻³

G = 6.67 × 10⁻¹¹ Nm⁻² kg⁻²

Time period of the satellite near the surface of the planet (h = 0) is

T =

=

= 5062.7 s

8. An earth’s satellite makes a circle around the earth in 90 minutes. Calculate the height of the satellite above the earth surface. Given radius of the earth is 6400 km and g = 980 cm⁻².

Solution:

Here T = 90 minutes

= 5400s,

R = 6400 km

= 6.4 × 10⁶ m

g = 980 cm^-2

= 9.8 ms^-2

As T = 2π

∴ R + h =

=

= 6.668 × 10⁶ m

= 6668 km

Hence h = 6668 – R

= 6668 – 6400

= 268 km

9. If the period of revolution of artificial satellite just above the earth surface T and the density of the earth be , then prove that is a universal constant. Also calculate the value of this constant.

Solution:

As T = 2π

=

M =

For the satellite revolving just above the earth’s surface, h = 0. So

M =

Also,

M =

∴ =

∴ = , which is a universal constant

And =

= 1.41 × 10¹¹ kgs² m⁻³

10. In a two stage launch of a satellite the first stage brings the satellite to a height of 150 km and second stage gives it the necessary critical speed to put it in a circular orbit around the earth. Which stage requires more expenditure of fuel? (neglect due to air resistance, especially in the first stage). Mass of the earth = 6.0 × 10²⁴ kg, radius = 6400 km, G = 6.67 × 10⁻¹¹ Nm² kg⁻².

Solution:

Work done on the satellite in first stage,

W₁ = P.E. at height of 150 km – P.E. at the surface of the earth

=

= GMm

=

Work done on the satellite in second stage,

W₂ = energy required to give its orbital velocity

=

=

=

=

=

=

As W₂ > W₁, so the second stage requires more expenditure of fuel.