Gravitational Potential Energy
When two bodies are placed close to one
another, they interact through the gravitational force. Due to this, they
possess mutual gravitational potential energy. When the distance between the
two bodies is changed, work is done either by the gravitational force between
the two bodies or against this force. In either case, the gravitational
potential energy of the bodies changes.
The
gravitational potential energy of a body is the energy associated with it due
to its position in the gravitational field of another body and is measured by
the amount of work done in bringing a body from infinity to a given point in
the gravitational field of the other.
When one body lies at infinity from another body, the
gravitational force on it is zero. Consequently its potential energy is zero.
This is called zero level of potential energy.
Expression for Gravitational Potential Energy:
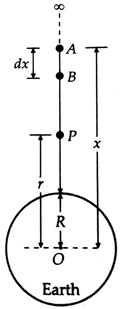
As shown in above figure, suppose the earth is a uniform Sphere of
mass 
and radius 
. We wish to calculate the potential
energy of a body of mass m located at point 
such that 
and 
.
Suppose at any instant the body is at point 
such that
= 
The gravitational
force of attraction on the body at 
is
F = 
The small work done
in moving the body through small distance 
is given by
= 
= 
The total work done
in bringing the body from infinity 
to a point will be 
will be
W = 
= 
= 
= 
= 
By
definition this work done is the gravitational potential energy 
of the body of mass 
located at distance 
from the centre of the earth.
U =
|
|
|
|
