Variation of g with Altitude (Height)

Effect of Altitude on g:

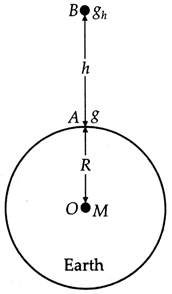
Consider the earth to be a sphere of mass M, radius R and centre O. Then the acceleration due to gravity at a point A on the surface of the earth will be

= ------ (i)

If  is the acceleration due to gravity at a point B at a height h from the earth's surface, then

= ------ (ii)

Dividing equation (ii) by (i), we get

=

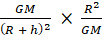
Effect of altitude on g.

=

=

=

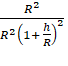
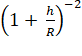
Expanding R.H.S. by using binomial theorem, we get

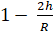= + terms containing higher powers of

If , then 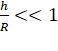, so that higher powers of can be neglected, we get

=

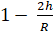
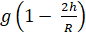= ------ (iv)

Both equations (iii) and (iv) show that the value of acceleration due to gravity decreases with the increase in height h, that is why the value of is less at mountains than at plains. While solving numerical problems, equation (iii) should be used when h is comparable to R and equation (iv) should be used when h << R.