Problems
1. First law of thermodynamics is
given by [CPMT 1977, 91]
a.
dQ
= dU + PdV
b.
dQ = dU × PdV
c.
dQ
= (dU + dV) P
d.
dQ
= PdU + dV
Solution: dQ = dU + PdV
ΔQ = ΔU + ΔW and ΔW = PΔV
2. If a system undergoes
contraction of volume then the work done by the system will be [BHU 1999]
a.
Zero
b.
Negligible
c.
Negative
d.
Positive
Solution: Negative.
ΔW = PΔV,
here DV is negative so DW will be negative.
3. The internal energy of an ideal gas
depends up on [RPMT 1997; MP
PMT 1999; CPMT 2003]
a.
Specific
volume
b.
Pressure
c.
Temperature
d.
Density
Solution: Temperature.
4. In changing the state of thermodynamics from
A to B state, the heat required is Q and the work done by the system is W. The change in its internal energy is [MP PMT 1986; AMU (Med.) 2001]
a.
Q + W
b.
Q − W
c.
Q
d.
![]()
Solution: Q
+ W
ΔQ
= ΔU + ΔW
ΔU
= ΔQ − ΔW
= Q + W (using proper sign)
5. Heat given to a system is 35 joules and work done by
the system is 15 joules. The change in the internal energy of the system will
be [MP PET/PMT 1988]
a. 50 J
b. 20 J
c. 30 J
d. 50 J
Solution: 20 J
ΔU = ΔQ − W
= 35 −15
= 20 J
6. The temperature of an ideal gas is kept constant as it
expands. The gas does external work. During this process, the internal energy
of the gas [MP PMT 1990]
a. Decreases
b. Increases
c. Remains constant
d. Depends on the molecular motion
Solution: Remains
constant
Internal energy depends only on the
temperature of the gas.
7. The first law of thermodynamics is concerned with the
conservation of [MP PMT 1987; CBSE PMT 1990, 92; AFMC 1997; CPMT 1999; BHU
1999; DCE 2000; BCECE 2003]
a. Momentum
b. Energy
c. Mass
d. Temperature
Solution: Energy
8. A thermodynamic system goes from states (i) P1, V to 2P1, V (ii) P, V to P,
2V. Then work done in the two cases is [MP PMT 1990]
a. Zero, Zero
b. Zero, PV1
c. PV1, Zero
d. PV1, P1V1
Solution: Zero,
PV1
(i) Case →
Volume = constant
⇒ ![]() = 0
= 0
(ii) Case → P = constant
⇒ ![]() = P
= P![]() = PV1
= PV1
9. If the amount of heat given to a system be 35 joules
and the amount of work done by the system be −15joules, then the change
in the internal energy of the system is [MP
PMT 1989]
a. −50 joules
b. 20 joules
c. 30 joules
d. 50 joules
Solution: 50 joules
ΔQ = ΔW + ΔU
35 = −15 + ΔU
ΔU = 50J
10. Work done on or by a gas,
in general depends upon the
a.
Initial state only
b.
Final state only
c.
Both initial and final states only
d.
Initial state, final state and the path
Solution: Initial state, final state and
the path
Work done = ![]() , which is state dependent as well as
path dependent.
, which is state dependent as well as
path dependent.
11. If R = universal gas constant, the amount of
heat needed to raise the temperature of 2 mole of an ideal monoatomic gas from
273K to 373K when no work is done [MP PET 1990]
a.
100 R
b.
150 R
c.
300 R
d.
500 R
Solution: 300
R
ΔQ = ΔU + ΔW (∵
ΔW = 0)
ΔQ = ΔU
= ![]() μRΔT
μRΔT
= 32 × 2 R(373 − 273)
= 300R.
12. Find the change
in internal energy of the system when a system absorbs 2 kilocalorie of heat
and at the same time does 500 joule of
work [EAMCET 1984]
a.
7900 J
b.
8200 J
c.
5600 J
d.
6400 J
Solution: 7900
J
ΔQ
= 2 kcal
= 2 × 103 × 4.2 J
= 8400 J
ΔW
= 500J
Hence from
ΔQ
= ΔU + ΔW
ΔW
= ΔQ − ΔU
= 8400 − 500
= 7900 J
13. A system performs
work ΔW when an amount of heat
is ΔQ added to the system, the
corresponding change in the internal energy is ΔU. A unique function of the initial and final states (irrespective
of the mode of change) is [CPMT
1981; J & KCET 2004]
a.
ΔQ
b.
ΔW
c.
ΔU and ΔQ
d.
ΔU
Solution: ΔU
Change in internal energy ΔU depends upon initial an
find state of the function while ΔQ and ΔW are path dependent also.
14. A container of volume 1m3is divided into two equal
compartments by a partition. One of these compartments contains an ideal gas at
300 K. The other compartment is vacuum. The whole system is thermally isolated
from its surroundings. The partition is removed and the gas expands to occupy
the whole volume of the container. Its temperature now would be [Manipal
MEE 1995]
a. 300 K
b. 239 K
c. 200 K
d. 100 K
Solution: 300 K
This is the case of free expansion and in this case ΔW=0, ΔU=0. So temperature
remains same i.e. 300 K.
15. 110 J of heat is added to a gaseous
system, whose internal energy change is 40 J, then the amount of external work
done is [CBSE PMT 1993; DPMT 1996, 03; AFMC 1999;
JIPMER 2000; MH CET 2000; Pb. PMT 2003]
a.
150 J
b.
70 J
c.
110 J
d.
40 J
Solution: 70
J
ΔQ
= ΔU + ΔW
ΔW
= ΔQ ΔU
= 100
− 40
= 70
J
16. Which of the following is not
thermodynamical function [CBSE PMT 1993; CPMT 2001; DCE 1996; 2001]
a. Enthalpy
b. Work done
c. Gibb's energy
d. Internal energy
Solution: Work done
Work done is not a thermodynamical
function.
17. When the amount of work done is 333 calorie and change
in internal energy is 167 calorie, then the heat supplied is [AFMC 1998]
a. 166 calorie
b. 333 calorie
c. 500 calorie
d. 400 calorie
Solution: 500 calorie
ΔQ = ΔU + ΔW
= 167 + 333
= 500 calorie
18. First law thermodynamics states that [KCET 1999]
a. System can do work
b. System has temperature
c. System has pressure
d. Heat is a form of energy
Solution: Heat is a
form of energy
Heat always refers
to energy in transit from one body to another because of temperature
difference.
19. A thermo-dynamical system is changed from state (P1,
V1) to (P2, V2) by two different process. The quantity
which will remain same will be [RPET 1999]
a. ΔQ
b. ΔW
c. ΔQ+ΔW
d. ΔQ−ΔW
Solution: ΔQ−ΔW
Change in internal energy does not depend upon path so
ΔU=ΔQ−ΔW remain constant.
20. In thermodynamic process, 200 Joules of heat is given
to a gas and 100 Joules of work is also done on it. The change in internal
energy of the gas is[AMU (Engg.)
1999]
a. 100 J
b. 300 J
c. 419 J
d. 24 J
Solution: 300 J
ΔQ = ΔU + ΔW;
ΔQ = 200 J
ΔW = −100 J
ΔU = ΔQ −
ΔW
= 200 − (−100)
= 300 J
21. A perfect gas contained in a cylinder is kept in
vacuum. If the cylinder suddenly bursts, then the temperature of the gas [MH CET 1999]
a. Remains constant
b. Becomes zero
c. Increases
d. Decreases
Solution: Remains constant
During free expansion of a perfect gas
no, work is done and also no heat is supplied from outside. Therefore, no
change in internal energy. Hence, temperature remain constant.
22. If 150 J of heat is added to a system and the work
done by the system is 110 J, then change in internal energy will be [AMU (Engg.)
1999; BHU 2000]
a. 260 J
b. 150 J
c. 110 J
d. 40 J
Solution: 40 J
ΔQ
= ΔU + ΔW
ΔU
= ΔQ − ΔW
= 150 − 110
= 40 J
23. If ΔQ and
ΔW represent the heat supplied to the system and the work done on the
system respectively, then the first law of thermodynamics can be written as [Roorkee 2000]
a.
ΔQ = ΔU + ΔW
b.
ΔQ = ΔU −
ΔW
c.
ΔQ = ΔW −
ΔU
d.
ΔQ = − ΔW
− ΔU
where
ΔU is the internal energy
Solution: ΔQ = ΔU −
ΔW
From FLOT ΔQ = ΔU + ΔW. Q Heat
supplied to the system so ΔQ is
Positive and work is done on the system so ΔW is Negative. Hence ΔQ = ΔU ΔW
24. For free expansion of the gas
which of the following is true [AMU (Med.) 2000]
a. Q = W = 0 and ΔEint
= 0
b. Q = 0, W > 0
and ΔEint
= −W
c. W = 0 =, Q >
0, and ΔEint
= Q
d. W > 0, Q <
0 and ΔEint
= 0
Solution: Q = W = 0 and ΔEint=0
25. Which of the following cannot determine the
state of a thermodynamic system [AFMC 2001]
a.
Pressure and
volume
b.
Volume and
temperature
c.
Temperature
and pressure
d.
Any one of
pressure, volume or temperature
Solution: Any one of pressure, volume or temperature. State of a thermodynamic state cannot determine
by a single variable (P or V or T)
26. Which of the following
is not a thermodynamics co-ordinate [AIIMS 2001]
a.
P
b.
T
c.
V
d.
R
Solution: R
R is the universal gas
constant.
27. Which of the following is
incorrect regarding the first law of thermodynamics [AIEEE 2005]
a.
It introduces the concept of the internal energy
b.
It introduces the concept of the entropy
c.
It is not applicable to any cyclic process
d.
None of the above
Solution: It introduces the concept
of the entropy. Entropy is related to second law of thermodynamics.
28. If a system undergoes contraction of volume then the work done by the
system will be [BHU 1999]
a.
Zero
b.
Negligible
c.
Negative
d.
Positive
Solution: Negative
ΔW=PΔV; here ΔV is negative
so ΔW will be negative.
29. A perfect gas goes from state A to
another state B by absorbing 8×105J of heat and doing 6.5×105J of external
work. It is now transferred between the same two states in another process in
which it absorbs 105J of heat. Then in the second process [BHU
1997]
a. Work done on the gas is 0.5×105J
b. Work done by gas is 0.5×105J
c. Work done on gas is 105J
d. Work done by gas is 105J
Solution: Work done on the gas is 0.5×105J
In first process
using ΔQ=ΔU+ΔW
8 × 105=ΔU+6.5×105
ΔU=1.5×10
Since final and initial states are same in both process.
So ΔU will be same in both process. For second process using
ΔQ=ΔU+ΔW
105=1.5×105+ΔW
ΔW=−0.5×105J
30. The state of a thermodynamic system is represented by [MH
CET 2004]
a. Pressure only
b. Volume only
c. Pressure, volume and temperature
d. Number of moles
Solution: Pressure, volume and temperature
31. In a thermodynamics process, pressure of
a fixed mass of a gas is changed in such a manner that the gas releases 20 J of
heat and 8J of work is done on the gas. If the initial internal energy of the
gas was 30J. The final internal energy will be
[DPMT 2002]
a.
18J
b.
9J
c.
4.5J
d.
36J
Solution: 18J
Given
ΔQ = −20J,
ΔW =
−8J
U1 = 30J
ΔQ =
ΔU+ΔW
ΔU = (ΔQ−ΔW)
(Uf − Ui)
= (Uf−30)
= −20− (−8)
Uf = 18J
32. If heat given to a system is 6 kcal and work done is 6 kJ.
Then change in internal energy is
[BHU Med. 2000]
a. 19.1 kJ
b. 12.5 kJ
c. 25 kJ
d. Zero
Solution: 19.1 kJ
ΔQ=ΔU+ΔW
ΔU=ΔQ−ΔW
=6×4.18−6
=19.08kJ
≈19.1kJ
33. Temperature is a measurement of coldness or hotness of an
object. This definition is based on [RPET 2003]
a. Zeroth law of thermodynamics
b. First law of thermodynamics
c. Second law of thermodynamics
d. Newton's law of cooling
Solution: Zeroth law of thermodynamics
34. If CV=4.96cal/mole K, then increase in internal energy when
temperature of 2 moles of this gas is increased from 340 K to 342 K [RPET 1997]
a. 27.80 calorie
b. 19.84 calorie
c. 13.90 calorie
d. 9.92 calorie
Solution: 19.84 calorie
ΔU=μCVΔT=2×4.96×
(342−340)=19.84 calorie.
35. First law of
thermodynamics is a special case of [CPMT 1985; RPET 2000; DCE 2000; CBSE PMT
2000; AIEEE 2002; AFMC 2002]
a.
Newton's law
b.
Law of conservation of energy
c.
Charle's law
d.
Law of heat exchange
Solution: Law of conservation of energy
Heat supplied to a gas raise its internal energy and does
some work against expansion, so it is a special case of law of conservation of
energy.
36. Out of the
following which quantity does not depend on path [RPET 2002]
a.
Temperature
b.
Energy
c.
Work
d.
None of these
Solution: Temperature
37. Liquid oxygen at
50 K is heated to 300 K at constant pressure of 1 atm. The rate of heating is
constant. Which one of the following graphs represents the variation of temperature
with time?
a.
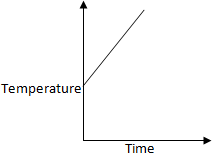
b.
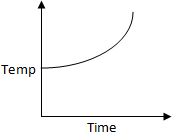
c.
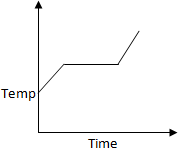
d.
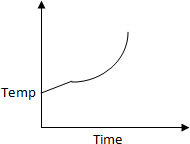
Solution:

At first temperature will increase then there
will be state change from liquid to gas.
38. The door of an
operating refrigerator is opened. Now the temperature of the room will
a. Increase
b. Decrease
c. Remain unchanged
d. Decrease in summer and increase in winter
Solution: Increase
Use first law of thermodynamics.
39. An ideal gas undergoes an isothermal change in volume with
pressure. Then
a. ![]()
b. ![]()
c. ![]()
d. PV = constant
Solution: PV = constant
For the special case of a gas to which Boyle's law applies, the
product PV is a constant if the gas is kept at isothermal conditions. The value
of the constant is nRT.
40. In changing the state of thermodynamics from A to B state,
the heat required is Q and the work done by the system is W. the change is its
internal energy is
a. Q + W
b. Q W
c. ![]()
d. Q
Solution: Q W
Use dQ = dU
+ dW.
41. An adiabatic process occurs at constant
a. Temperature
b. Pressure
c. Heat
d. Temperature and pressure
Solution: Heat
42. Pressure-temperature
relationship for an ideal gas undergoing adiabatic change is
a. ![]()
b. ![]()
c.
![]() = constant
= constant
d.
![]()
Solution: ![]()
For adiabatic process
PVγ = constant -- (1)
and the combined gas law: PV/T = constant -- (2)
putting V from (2) to (1)
P(T⁄P)γ = constant
P(γ-1)Tγ =
constant
43. The gas law ![]() = constant is true for
= constant is true for
a. Isothermal
changes only
b. Adiabatic
changes only
c. both
isothermal and adiabatic changes
d. Neither
isothermal nor adiabatic changes
Solution: Both isothermal and adiabatic changes
The Gas law is true for both
isothermal and adiabatic changes.
44. A gas behaves more closely
as an ideal gas at:
a. Low pressure and low temperature
b. Low pressure and high
temperature
c. High pressure and low
temperature
d. High pressure and high
temperature
Solution: Low pressure and high
temperature
45. A block of a mass 100 g slides
on a rough horizontal surface. If the speed of the block decreases from 10m/s
to 5m/s the thermal energy developed in the process is:
a. 3.75 J
b. 37.5 J
c. 0.375 J
d. 0.75 J
Solution: 3.75 J
Thermal energy = loss in kinetic
energy
=![]() m (
m (![]()
![]()
=![]()
=3.75J
46. A thermodynamic system
undergoes cyclic process ABCDA as shown in Fig. The work done by the system in
the cycle is[ AIPMT 2014]
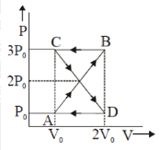
a. ![]()
b. Zero
c.
P0V0
d. 2 P0V0
Solution:
P0V0
P0V0Work in COB = (-P0) V
Work in AOD = P0V0
Total work = Work in COB + Work
in AOD =0.
47. During an adiabatic process,
the pressure of a gas is found to be proportional to the cube of its
temperature. The ratio of ![]() for the gas is
for the gas is
a. ![]()
b. 2
c. ![]()
d. ![]()
Solution: ![]()
P ∝ T3
PV = nRT
PV=C (P) ![]()
C=constant
P ![]() V=C
V=C
PV ![]() =C
=C
On comparing above equation with
P (V) γ= Constant
We get γ = 3/2.
48. The change in internal
energy, when a gas is cooled from 927°C to 27°C
a. a)200%
b. b) 100%
c. c)300%
d. d) 400%
Solution:
300%
Energy of gas E ∝ T
Let T1=927 + 273=1200 K
T2=27 + 273=300%
49. A sample of Oxygen gas and a
sample of Hydrogen gas both have the same mass, the same volume and the same
pressure. The ratio of their absolute temperature is
a. 1:4
b. 4:1
c. 1:16
d. 16:1
Solution: 16:1
PV=nRT
PV= ![]() RT
RT
PV= ![]() RT1 and PV =
RT1 and PV = ![]() RT2
RT2
![]() =
=![]()
![]() =16:1
=16:1
50. A system goes from A to B
via two process I and II as shown in figure. If ΔU1 and ΔU2 are the
changes in internal energies in the process I and II respectively, then [AIEEE
2005]
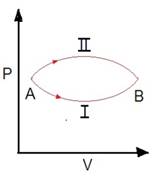
a) Relation between ΔU1 and ΔU2 cannot be determined
b) ΔU1 = ΔU2
c) ΔU2 < ΔU1
d) ΔU2 > ΔU1
Solution: ΔU1 = ΔU2
Change in internal energy do not
depend upon the path followed by the process. It only depends on initial and
final states i.e. ΔU1 = ΔU2
51. "Heat cannot by itself
flow from a body at lower temperature to a body at higher temperature" is
a statement or consequence of
a.
First law of thermodynamics
b.
Second law of thermodynamics
c.
Conservation of momentum
d.
Conservation of mass.
Solution: Second law of thermodynamics.
Heat cannot flow itself from a
lower temperature to a body of higher temperature. This corresponds to second
law of thermodynamics.
52. The first law of
thermodynamics is a restatement of the
a. Law of conservation of momentum
b. Newton's law of cooling
c. Law of conservation of mass
d. Law of conservation of energy
Solution: Law of conservation of energy
The First Law of Thermodynamics
is simply a restatement of the Law of Conservation of Energy. There are a few
ways of stating it, but they all mean the same thing:
"Energy is neither created
nor destroyed. It can only change form."
"The change in the system's
thermal energy is equal to the heat added to the system minus the work done by
the system."
53. In an adiabatic process,
there is no
a. change in temperature
b. exchange of heat
c. change in internal energy
d. work done
Solution: Exchange of heat
In thermodynamics, an adiabatic process is one that
occurs without transfer of heat or matter between a thermodynamic system and
its surrounding. In an adiabatic process, energy is transferred only as work.
54. On a cold morning, a metal surface on touching is felt colder
than a wooden surface, because the metal has:
a. low thermal conductivity
b. high thermal conductivity
c. high specific heat
d. low specific heat
Solution: High
thermal conductivity
Metal is a good conductor of heat. Ona cold morning, a
metal surface on touching is felt colder than wood because metal is a good conductor
of heat (high thermal conductivity) hence, when we touch metal, the metal
rapidly conducts heat from our hand and gives a cold feeling. Wood on the
conducts heat is a bad conductor of heat, it conducts heat slowly from our hand
and appears less cold.
55. The processes or systems that do not involve heat are
called
a. Isothermal processes
b. Equilibrium processes
c. Thermal processes
d.
Adiabatic processes
Solution: Adiabatic processes
56. In an open system, for maximum work, the process must be
entirely
a. Irreversible
b. Reversible
c. Adiabatic
d. None of the mentioned
Solution: Reversible
A
reversible process gives the maximum work.
57. During the adiabatic compression of a gas, its temperature
will
a.
Falls
b.
Remains constant
c.
Rises
d.
Becomes zero
Solution: Rises
The
work done on the gas during adiabatic process increases its internal energy and
hence its temperature rises.
58. The work done on the gas
during adiabatic process increases its internal energy and hence its
temperature rises.
a.
![]()
b. ![]()
c. PV
d. ![]()
Solution: ![]()
∆U = ![]()
=![]()
59. A Carnot
engine having an efficiency of ![]() as heat engine, is used as a refrigerator. If
the work done on the system is 10 J, the amount of energy absorbed from the reservoir
at lower temperature is
[NEET 2017]
as heat engine, is used as a refrigerator. If
the work done on the system is 10 J, the amount of energy absorbed from the reservoir
at lower temperature is
[NEET 2017]
a) 1 J
b) 90 J
c) 99 J
d) 100 J
Solution: 90 J
Efficiency of the Carnot Engine η =![]()
=![]()
=![]()
Qinput =100J
Qoutput =![]() 100J = 90J
100J = 90J
This Qinput is
the amount of energy that will be absorbed when this Carnot engine is used
as a refrigerator.
60. Thermodynamic processes are indicated in
the following diagram. Match the following
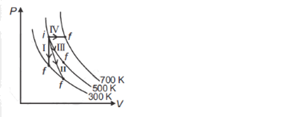
|
Column-1 |
Column-2 |
|
Process
I |
Isochoric |
|
Process
II |
Adiabatic |
|
Process
III |
Isothermal |
|
Process
IV |
Isobaric |
a. P → a, Q → c, R → d, S → b
b. P → c, Q → a, R → d, S → b
c. P → c, Q → d, R → b, S → a
d. P → d, Q → b, R → a, S → c
Solution: P
→ c, Q → a, R → d, S → b
Process I = Isochoric
Process II = Adiabatic
Process III = Isothermal
Process IV = Isobaric
61. A given sample of an ideal gas occupies a
volume V at a pressure P and absolute
temperature T. The mass of each
molecule of the gas is m. Which of
the following gives the density of the gas? [NEET II 2016]
a. ![]()
b. mkT
c. ![]()
d. ![]()
Solution: ![]()
Density = ![]() =
= ![]()
= ![]()
= ![]()
62. In a thermodynamic process, pressure of a
fixed mass of a gas is changed in such a manner that the gas released 20 J of
heat and 8 J of work has done on the gas. If the initial internal energy of the
gas was 30 J, then the final internal energy will be
a.
58J
b.
2J
c.
42J
d.
18J
Solution: 18J
![]() =
= ![]() +
+![]()
= 30 -20 +8
= 18J
63. One mole of an ideal monatomic gas
undergoes a process described by the equation PV3 = constant. The heat capacity of the gas during this
process is [NEET II 2016]
a.
2 R
b.
R
c.
3![]()
d.
5![]()
Solution: R
PV3 = constant.
For a poly tropic process, PVα = constant
𝐶=𝐶𝑣+![]()
=![]() +
+![]()
=![]() -
-![]()
=R
64. A gas is compressed isothermally to half
its initial volume. The same gas is compressed separately through an adiabatic
process until its volume is again reduced to half. Then [AIPMT 2015]
a. Compressing the gas isothermally will require more work
to be done
b. Compressing the gas through adiabatic process will
require more work to be done.
c. Compressing the gas isothermally or adiabatically will
require the same amount of work.
d. Which of the case (whether compression through isothermal
or through adiabatic process) requires more work will depend up on the
atomicity of the gas.
Solution: Compressing the gas through adiabatic process will
require more work to be done

65. An ideal gas is compressed to half its
initial volume by means of several processes. Which of the process results in
the maximum work done on the gas?
a. Isothermal
b. Adiabatic
c. Isobaric
d. Isochoric
Solution: Adiabatic
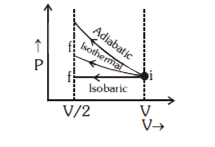
Work done on the gas
Wisochoric = 0, then
Wadiabatic > Wisothermal > Wisobaric
66. The coefficient of performance of a
refrigerator is 5. If the temperature inside freezer is -20°C, the temperature
of the surroundings to which it rejects heat is:
[ReAIPMT 2015]
a) 21°C
b) 31°C
c) 41°C
d) 11°C
Solution: 31°C
Coefficient of performance of refrigerator
COP =![]()
Where TL → lower temperature
TH →higher temperature
![]() =5
=5
TH =![]() TL =
TL =![]() (253)
(253)
= 303.6k
67. Two vessels separately contain two ideal gases
A and B at the same temperature, the pressure of A being twice that of B. Under
such conditions, the density of A is found to be 1.5 times the density of B.
The ratio of molecular weight of A and B is [REAIPMT 2015]
a. ![]()
b. ![]()
c. 2
d. ![]()
Solution: ![]()
According to ideal gas equation
![]() =
=![]()
= (1.5) (![]() )
)
= ![]()
68. The ratio of the specific heats γ=![]() in
terms of degrees of freedom (n) is given by:
[AIPMT 2015]
in
terms of degrees of freedom (n) is given by:
[AIPMT 2015]
a. ![]()
b. ![]()
c. ![]()
d. ![]()
Solution: ![]()
The specific heat of gas at
constant volume in terms of degree of freedom 'n' is:
Cv =![]() R
R
Cp - Cv = R
Cp =![]() R + R
R + R
=R![]()
![]() =
=![]() =
=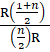
= ![]()
69. One mole of an ideal diatomic gas undergoes
a transition from A to B along a path AB as shown in the figure, then the
change in internal energy of the gas during the transition is: [ NEET 2015]
a. -12 kJ
b. 20 kJ
c.
20 kJ
d. 20 J
Solution: 20 kJ

The charge in internal energy of gas in the transition
from A to B is
![]() =nCvdT
=nCvdT
= nR![]()
=![]() (2
(2 ![]() 103
103 ![]() 6 - 5
6 - 5 ![]() 103
103 ![]() 4 )
4 )
= - ![]()
= - 20 KJ
70. A monoatomic gas at a pressure P, having
a volume V expands isothermally to a volume 2V and then adiabatically to a volume
16V.The final pressure of the gas is
. (Take γ = 5/3)[AIPMT 2014]
a. ![]()
b. 16P
c. 64P
d. 32P
Solution: ![]()
P1V1=P2V2
P2 = P1![]() =
=![]()
P3=P2![]()
=![]()
=![]()
P3 =![]()
71. In the given (V
T) diagram, what is the relation between pressures P1 and P2?
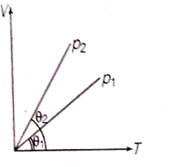
a. P2 = P1
b. P2 > P1
c. P2 < P1
d. Cannot be predicted
Solution: P2
< P1
The slope of the graph directly proportional to ![]()
72. The efficiency of carnots engine operating between two reservoirs, maintained
at temperature 27° C and -123° C is
a. 0.5
b. 0.4
c.0.6
d.0.25
Solution: 0.5
η = 1 -![]()
= 1 ![]()
=0.4229
=0.5
73. A gas is taken through the cycle A → B → C → A, as shown. What is the net
work done by the gas?
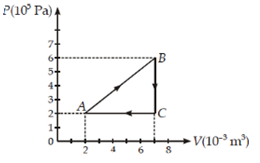
a. 2000 J
b. 1000 J
c. Zero
d. 2000 J
Solution: 1000 J
Work done = area enclosed under the curve
= ![]() J
J
= 1000J
74. The molar specific heats of an ideal gas
at constant pressure and volume are denoted by Cp
and Cv
respectively. If γ=![]() and R is
the universal gas constant, then Cv
is equal to
[NEET 2013]
and R is
the universal gas constant, then Cv
is equal to
[NEET 2013]
a. ![]()
b. ![]()
c. ![]()
d.
![]()
Solution: ![]()
Cv(γ-1) =R
Cp-Cv = R
From given Cp = γCv
γCv Cv = R
Cv(γ-1) =R
Cv = ![]()
74. An ideal gas exerts a pressure P. The
mean kinetic energy per unit volume is E. Which of the following relations is
correct.
a. P=E
b. P=![]()
c. P=![]() E
E
d. P=![]() E
E
Solution: P=![]() E
E
K.E= ![]()
![]() =
= ![]()
75. The change in internal energy, when a gas
is cooled from 927°C to 27°C
a. 200%
b. 100%
c. 300%
d. 400%
Solution: 300%
We know that Energy of gas E ∝ T
Let T1=927 + 273=1200 K
T2=27 + 273=300 K
76. Four molecules of gas are having speeds
of 1, 4, 8 and 16 ms-1. The root mean square velocity of the gas
molecules is
a. 7.25 ms-1
b. 52.56 ms-1
c. 84.25 ms-1
d. 9.2 ms-1
Solution: 9.2 ms-1
C = ![]() ms-1
ms-1
= ![]() ms-1
ms-1
=9.2 ms-1
77. At room temperature the r.m.s speed of the molecules of certain diatomic gas is
found to be 1933 ms-1. The gas is
a) H2
b) F2
c) O2
d) Cl2
Solution: H2
M = ![]()
= ![]()
= 0.002Kg
M = 2gms
∴ H2
78. By what percentage should the pressure of
a given mass of gas be increased so as to decrease its volume by 10% at
constant temperature?
a. 8.1%
b. 9.1%
c. 10.1%
d. 11.1%
Solution: 11.1%
Using Boyle's law
PV = P'× (0.9V)
P'= (10/9)P=1.111P
Thus Increase in P=11.1%
79. A sample of Oxygen gas and a sample of
Hydrogen gas both have the same mass, the same volume and the same pressure.
The ratio of their absolute temperature is
a. 1:4
b. 4:1
c. 1:16
d. 16:1
Solution: 16:1
PV = nRT
PV = ![]() RT
RT
PV = R![]() T1 and PV=
T1 and PV= ![]() RT2
RT2
Thus
![]() =
= ![]()
![]() =16:1
=16:1
80. At what temperature is the root mean
square velocity of gaseous hydrogen molecules equal to that of oxygen molecules
at 47°C?
a. 20 K
b. 80 K
c. -73 K
d. 3 K
Solution: 20 K
T = 273+47 = 320K
M0 = 32
T = ![]()
= 20K
81. One kg of diatomic gas is at a pressure
of 8×104N/m2. The density of the gas is 4kg/m3. What is the energy
of the gas due to thermal motion? [AIEEE 2009]
a. 5×104J
b. 6×104J
c. 7×104J
d. 3×104J
Solution: 5×104J
Volume=![]()
=![]() m3
m3
Degree of freedom of diatomic gas=5
K.E.=![]() PV
PV
K.E.= ![]() ×8×104
×
×8×104
×![]()
=5×104 J
82. If Cp
and Cv denotes
the specific heats of nitrogen per unit mass at constant pressure and constant
volume respectively then. [AIEEE 2007]
a. Cp - Cv=28R
b. Cp - Cv=![]()
c. Cp - Cv=![]()
d. Cp - Cv=R
Solution: Cp - Cv=![]()
CvCp = ![]()
Cp Cv
= R
Cp Cv
= ![]()
83. The work of 146kJ is performed in order
to compresses one kilo mole of gas adiabatically and in this process the temperature
of the gas increased by 7°C. The gas is (R=8.3 J mol-1K-1) [AIEEE 2006]
a. diatomic
b. triatomic
c. a mixture of monoatomic and diatomic
d. monoatomic
Solution: diatomic
For adiabatic process,
dQ = 0
dU =![]()
nCvdT= +146×103 J
![]() ×7 =+146×103
×7 =+146×103
![]() =+146×103
=+146×103
f= 5.02=5
So, it is a diatomic gas.
85. During an adiabatic process, the pressure
of a gas is found to be proportional to the absolute temperature. The ratio ![]() for
the gas is
for
the gas is
a.
![]()
b.
![]()
c.
![]()
d.
![]()
Solution: ![]()
P![]() T5, an adiabatic process P
T5, an adiabatic process P![]() T
T![]()
86. For an
isothermal expansion of a perfect gas, the value of ![]() is
equal to
is
equal to
a.
![]()
b.
![]()
c.
![]()
d.
![]()
Solution: ![]()
PV =
Constant
P![]() V- V
V- V![]() P = 0
P = 0
87. If r denotes the ratio of adiabatic of two
specific heats of a gas. Then what is the ratio of slope of adiabatic and
isothermal P→V curves at their point of intersection?
a.
![]()
b.
γ 1
c.
γ
d.
γ + 1
Solution: γ
For isothermal process, PV = constant
∴
P ΔV VΔP = 0
i.e.
![]() =
= ![]() -----
(1)
-----
(1)
For adiabatic process PVγ
= constant
PγV(γ1) ΔV + Vγ
ΔP = 0
∴
γV(γ1) ΔV = ![]()
∴
![]() =
=![]()
(ΔP / P) = [( γ ΔV) / V]
i.e.
(ΔP / ΔV) = γ (P/V) -----
(2)
At point of intersection, slopers
ratio is
![]() =
= ![]()
![]() =
γ
=
γ
88. A container that suits the occurrence of
an isothermal process should be made of
a.
wood
b.
coppers
c.
glass
d.
cloth
Solution: coppers
An isothermal process that takes place at constant
temperature, must be carried out in a vessel with conducting wall so that heat
generated should go out at once.
89. A thermodynamic process in which
temperature T of the system remains constant throughout variable P and V may
change is called
a. Isothermal process
b. Isochoric process
c. Isobaric process
d. None of this
Solution: Isothermal process
90. The volume of an ideal gas is 1 liter
column and its pressure is equal to 72 cm of Hg. The volume of gas is made 900
cm3 by compressing it isothermally. The stress of the gas will be
a.
4cm
b.
6cm
c.
7cm
d.
8cm
Solution: 8cm
Given:
Initial pressure on gas P1=72cm of
Hg
Initial volume of gas =V1=1L
Final volume of gas=V2=9L
Let P2 be the final pressure on
Gas
From Boyle's law: P1V1=P2V2
P2=![]()
=72x![]()
=8cm of Hg.
91. In adiabatic expansion the initial value
will be
a. ∆U = 0
b. ∆U =
Positive
c. ∆U =
Negative
d. ∆W = 0
Solution: ∆U =
Negative.
92. The pressure and density of a diatomic gas γ = ![]() then, Change adiabatically from (p, d) to (p1,
d1) if
then, Change adiabatically from (p, d) to (p1,
d1) if ![]() = 32 then
= 32 then ![]() should be
should be
a. 128
b. ![]()
c. 32
d. None of this
Solution: 128
![]() =
= ![]()
![]() =
= ![]() = (32)7/5
= (32)7/5
= 128
93. An engine is supposed to operate between two reservoirs
at temperature 727° C and 227° C. The maximum possible efficiency of such an
engine is
a.
![]()
b.
![]()
c.
![]()
d.
1
Solution: ![]()
n = 1 -![]()
=1-![]()
=![]()
94. A gas expands 0.25m3 at constant pressure
103 ![]() the work done is
the work done is
a. 250 J
b. 2.5 erg
c. 250 W
d. 250 N
Solution: 250 J
![]() =P
=P![]() V = 103 × 0.25
V = 103 × 0.25
=250 J
95. The volume of air increases by 5% in an adiabatic expansion.
The percentange decrease in its pressure will be
a. 5%
b. 6%
c. 7%
d. 8%
Solution: 7%
PVγ = K or pγVγ-1dV+dP.Vγ
= 0
![]() ×100= -γ
×100= -γ![]()
= -1.4×5
=7%
96. For adiabatic process which relation is true
mentioned below? γ = ![]()
a. Pγ V = Constant
b. Tγ V = Constant
c. TVγ = Constant
d. TVγ-1
= Constant
Solution: TVγ-1 = Constant.
PV = RT
P = ![]()
![]() = Constant
= Constant
TV (γ-1) =
Constant.
97. For adiabatic process
which one is wrong statement?
a. dQ = 0
b. entropy is not constant
c. du = - dw
d. Q = Constant
Solution: Q = Constant
Internal energy of the
system can be constant, that is ∆U =
Constant but the quantity (Q) cannot be constant.
98. Carnot engine working
between a source temperature of T2 and sink temperature of T1
has efficiency of 25%. If the sink temperature is reduced by 20°C, the
efficiency is increased to 30%. Then the source and the sink temperature is
a. 400°C and 300°C
b. 300°C and 400°C
c. 200°C and 300°C
d. 300°C and 200°C
Solution: 400°C and 300°C
Efficiency, η = (T2
T1) / T2 = 25% = 0.25
Where T2 is the
source temperature and T1 is the sink temperature.
T2 T1
= 0.25 T2
T1 = 0.75 T2
In the second case, if the
sink is reduced by 20o C, then
η= T2 (T1
20) / T2 = 30% = 0.3
T2 T1
+ 20 = 0.3 T2
. (1)
Putting the value of T1 in equation (1), we will get:
T2 0.75 T2 + 20 = 0.3 T2
0.25 T2 + 20 = 0.3 T2
20 = 0.3 T2 0.25 T2 = 0.05 T2
T2 = 20 / 0.05 = 400°C
Hence, T1 = 0.75 T2
T1 = 0.75 X 400 = 300°C
Hence, temperature of the
source and the sink is 400o C and 300o C respectively.
99. A diatomic gas is used
in a carnot engine as the
working substance, if during the adiabatic expansion part of the cycle the
volume of the gas increases from V to 32V, the efficiency of the
engine is
a. 0.99
b. 0.75
c. 0.50
d. 0.25
Solution: 0.75
TV (γ-1) =
Constant.
TbVb(γ-1) = TcVc(γ-1) = [32](7/5)-1
= [25]2/5
Tb = 4Tc =
4
1- ![]() = 1 -
= 1 -![]() =
= ![]()
100. A carnot
s engine whose sink is at a temperature of 300 K has an efficiency of 40% by
space should the temperature of the source be increase the efficiency to 50% of
original efficiency?
a. a 275 K
b. 325 K
c. 300 K
d. 250 K
Solution: 250 K
Temperature of sink (Tc) = 300K
Temperature of source
= Th
Initial efficiency = 40%
Efficiency n1 =
1 - ![]()
0.4 = 1 - ![]()
Th1 = ![]() = 500K
= 500K
If we need to increase the
efficiency by 50% of original,
Efficiency = 40% +
(50/100) ×40% = 40%+20% = 60%
Efficiency n2 =
1 - ![]()
0.6 = 1 - ![]()
Th2 = ![]() = 750K
= 750K
Change in temperature =
750K 500K = 250K