Applications of Gauss’s Law

Gauss’s Law can be used to solve complex electrostatic problems involving unique symmetries like cylindrical, spherical or planar symmetry. Also, there are some cases in which calculation of electric field is quite complex and involves tough integration. Gauss’s Law can be used to simplify evaluation of electric field in a simple way.

We apply Gauss’s Law in following way:

Ø Choose a Gaussian surface, such that evaluation of electric field becomes easy.

Ø Make use of symmetry to make problems easier.

Ø Remember, it is not necessary that Gaussian surface to coincide with real surface that is, it can be inside or outside the Gaussian surface.

Electric Field due to Infinite Wire

Consider an infinitely long wire with linear charge density λ and length L. To calculate electric field, we assume a cylindrical Gaussian surface due to the symmetry of wire. As the electric field E is radial in direction; flux through the end of the cylindrical surface will be zero, as electric field and area vector are perpendicular to each other. The only flowing electric flux will be through the curved Gaussian surface. As the electric field is perpendicular to every point of the curved surface, its magnitude will be constant.

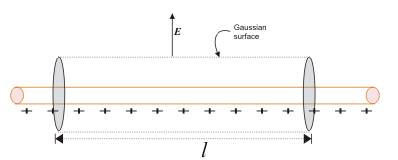
Cylindrical Gaussian surface of radius r and length l

Consider a Cylindrical Gaussian surface of radius r and length l.

The surface area of the curved cylindrical surface will be 2πrl. The electric flux through the curve will be

E × 2πrl

and

According to Gauss’s Law

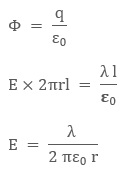
Vectorically, the above relation is

where  is radial unit vector pointing the direction of electric field .

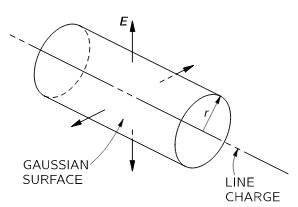
Direction of Electric field is radially outward in case of positive linear charge density

Note 1: Direction of the electric field will be radially outward if linear charge density is positive and it will be radially inward if linear charge density is negative.

Note 2: We considered only the enclosed charge inside the Gaussian surface

Note 3: The assumption that the wire is infinitely long is important because, without this assumption, the electric field will not be perpendicular to the curved cylindrical Gaussian surface and will at some angle with the surface.

Electric Field due to Infinite Plate Sheet

Imagine an infinite plane sheet, with surface charge density σ and cross-sectional area A. The position of the infinite plane sheet is given in the figure below:

Infinite Charge Sheet

The direction of the electric field due to infinite charge sheet will be perpendicular to the plane of the sheet. Let’s consider cylindrical Gaussian surface, whose axis is normal to the plane of the sheet. The electric field  can be evaluated from Gauss’s Law as

According to Gauss’s Law

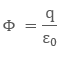
From continuous charge distribution charge q will be σ A. Talking about net electric flux, we will consider electric flux only from the two ends of the assumed Gaussian surface. This is because the curved surface area and an electric field are normal to each other, thereby producing zero electric flux. So the net electric flux will be

Φ = EA – (– EA)

Φ = 2EA

Then we can write

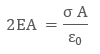
The term A cancel out which means electric field due to infinite plane sheet is independent of cross section area A and equals to

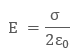
In vector form, the above equation can be written as

where is a unit vector depicting direction of electric field perpendicular and away from the infinite sheet.

Note 1: The direction of electric field is away from the infinite sheet if the surface charge density is positive and towards the infinite sheet if the surface charge density is negative.

Note 2: Electric field due to the infinite sheet is independent of its position.

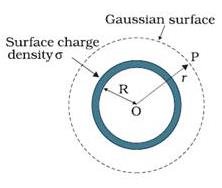
Electric Field due thin Spherical Shell

Consider a thin spherical shell of surface charge density σ and radius “R”. By observation, it’s obvious that shell has spherical symmetry. The electric field due to the spherical shell can be evaluated in two different positions:

1. Electric Field outside the Spherical Shell

2. Electric Field inside the Spherical Shell

Electric Field outside the Spherical Shell

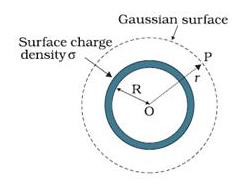
Spherical shell with point P outside

To find electric field outside the spherical shell, we take a point P outside the shell at a distance r from the center of the spherical shell. By symmetry, we take Gaussian spherical surface with radius r and center O. The Gaussian surface will pass through P, and experience a constant electric field  all around as all points is equally distanced “r’’ from the center of the sphere. Then,

According to Gauss’s Law

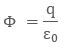
The enclosed charge inside the Gaussian surface q will be σ × 4 πR². The total electric flux through the Gaussian surface will be

Φ = E × 4 πr²

Then by Gauss’s Law, we can write

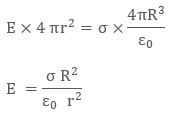
Putting the value of surface charge density σ as q/4 πR2, we can rewrite the electric field as

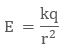
In vector form, electric field is

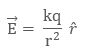
where is radius vector, depicting the direction of electric field.

Note: If the surface charge density σ is negative, the direction of the electric field will be radially inward.

Electric Field inside the Spherical Shell

Spherical shell with point P inside

To evaluate electric field inside the spherical shell, let’s take a point P inside the spherical shell. By symmetry, we again take a spherical Gaussian surface passing through P, centered at O and with radius r. Now according to Gauss’s Law

The net electric flux will be E × 4 π r². But the enclosed charge q will be zero, as we know that surface charge density is dispersed outside the surface, therefore there is no charge inside the spherical shell. Then by Gauss’s Law 

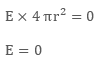
Note: There is no electric field inside spherical shell because of absence of enclosed charge.