Gauss’s Law
Gauss’s
Law
The Gauss Law, also known as Gauss theorem is a
relation between an electric field with the distribution of charge in the
system. The law was proposed by Joseph- Louis Lagrange in 1773 and
later followed and formulated by Carl Friedrich Gauss in 1813.
Gauss’s
Law states that the net electric flux is equal to 
times the
charge enclosed in it. Mathematically Gauss Law is expressed as
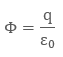
where
Φ is the net electric flux and q is the charge enclosed in it. The symbol
The integral
form of electric flux is
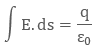
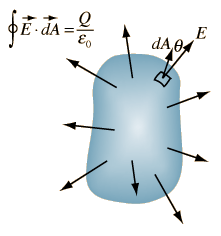
Gauss’s Law
where E
is the electric field flowing through small area element ds and q is the net
charge enclosed in it. This form is used when we calculate electric flux in
continuous charge distribution case. The surface, through which we calculate
electric flux is called Gaussian Surface.
Proof
of Gauss’s Law
Consider a sphere of enclosed charge q inside it,
placed at its center. The radius of the sphere is
‘r’. To prove Gauss’s Law, we need to find the net electric flux through the
sphere. This can’t be done directly as the surface area is non-uniform in
nature, otherwise we could have multiplied electric field with a surface area
of the sphere. So, to evaluate electric field we will divide the sphere into
small surface elements.
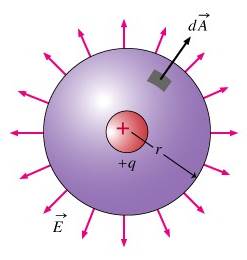
Dividing a sphere
into small surface area element dA
Now,
each small surface area will feel same electric field due to charge q placed
inside the sphere as each one is at equivalent distance ‘r’ from charge q.
Adding further, these small surface elements will create small electric flux as
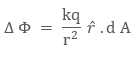
where 
is the electric
field produced by charge q on the small surface area element ds which is r
distance away from it.
Is
the direction vector, depicting the direction of electric field. As the direction
of electric field and small surface area element is in the same direction that
is, radially outwards, the small flux can be written as
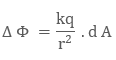
The
total electric flux of the sphere can be obtained by adding small flux through
all the small surface area elements.
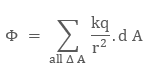
Since
electric field on each surface area element is same, it will come out of the
summation, that is,
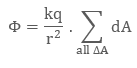
The
summation of all small area elements dA will give the total surface area A of the
sphere that is 4πr2.
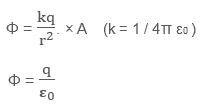
Note: The
net electric flux through closed surface is zero, as there is no charge inside
close surface.
Significance
of Gauss’s Law
The
most significant application of Gauss’s Law is that it is not only limited to
simple cases but can be used in a general form. We consider following points
while applying Gauss’s Law:
Ø Gauss’s Law is always valid for any closed surface,
irrespective of its shape that is, regular or irregular.
Ø We consider only the sum of charges which are present
inside the closed surface.
Ø The inside charge and outside charge of the closed
surface are responsible for electric field, but the electric flux will be due
to inside charge only.
|
|
|
|
