Capacitor
The
capacitor is a component which has the ability or “capacity” to store energy in
the form of an electrical charge producing a potential difference (Static Voltage)
across its plates, much like a small rechargeable battery.
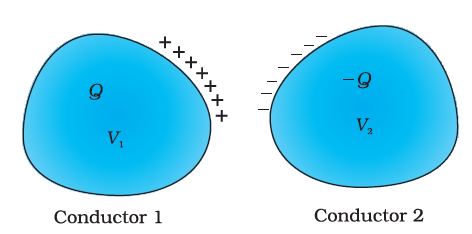
A capacitor is a system of two conductors
separated by an insulator. The conductors have charges, say Q1 and Q2, and potentials V1 and V2.
·
Usually,
in practice, the two conductors have charges Q and – Q, with potential difference V = V1 – V2 between them. We shall consider only this
kind of charge configuration of the capacitor. (Even a single conductor can be
used as a capacitor by assuming the other at infinity.)
·
The conductors may be so charged by connecting
them to the two terminals of a battery. Q is called the charge of the capacitor,
though this, in fact, is the charge on one of the conductors – the total charge
of the capacitor is zero. The electric field in the region between the
conductors is proportional to the charge Q. That is, if the charge on the capacitor
is, say doubled, the electric field will also be doubled at every point. (This
follows from the direct proportionality between field and charge implied by
Coulomb’s law and the superposition principle.)
·
Now,
potential difference V
is the work
done per unit positive charge in taking a small test charge from the conductor
2 to 1 against the field. Consequently, V is also proportional to Q, and the ratio Q/V is a constant

The
Capacitance of a Capacitor
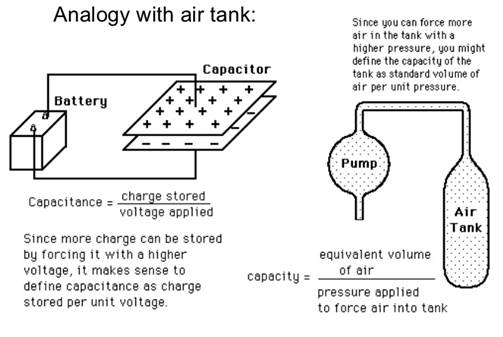
Capacitance is the electrical property of a
capacitor and is the measure of a capacitors ability to store an electrical
charge onto its two plates with the unit of capacitance being the Farad (abbreviated
to F) named after the British physicist Michael Faraday.
Capacitance is defined as being that a capacitor
has the capacitance of One Farad when a charge of One
Coulomb is stored on the plates by a voltage of One volt.
Note that capacitance, C is always positive in value and has no
negative units. However, the Farad is a very large unit of measurement to use
on its own so sub-multiples of the Farad are generally used such as
micro-farads, nano-farads and pico-farads,
for example.
Standard
Units of Capacitance
·
Microfarad (μF) 1μF = 1/1,000,000 = 0.000001
= 10-6 F
·
Nanofarad (nF) 1nF
= 1/1,000,000,000 = 0.000000001 = 10-9 F
·
Picofarad (pF) 1pF =
1/1,000,000,000,000 = 0.000000000001 = 10-12 F
Then
using the information above we can construct a simple table to help us convert
between pico-Farad (pF), to nano-Farad
(nF), to micro-Farad (μF) and to Farads (F).

Charging of Parallel Plate Capacitor
Circuit for charging capacitor
Let C be the two plates of
capacitor, V be the potential difference and k be the switch in above figure.
Now when the
key is closed then the electrons from the first plate start moving towards the
positive end of the battery that is, there is flow of electrons from negative
end to positive end of the battery
The electrons which moved towards
to the positive end of battery from there they will start moving towards to the
second plate. In this way both the plates will acquire charges, one will
acquire positive charge while other will acquire negative charge.
This process will continue until
the capacitor acquires potential difference V
in the exact same amount that of the battery. Now the process will stop. At
this time when the process has been stopped the capacitor has stored electric
charge on it with the potential difference which is same as battery.
So now the
charge can be written as:
Q
= CV
The amount of
electric charge stored in any of the plate of parallel plate capacitor is
directly proportional to the potential difference between the two plates of
Parallel Plate Capacitor. This relation can be seen as:
Q
α V
or
Q
= (constant) V
where,
C = Capacitance of capacitor
Q = Amount of charge stored in one capacitor
V = Potential difference
between the two plates
The capacitance
of parallel plate capacitor depends upon
·
The
distance d between two plates
·
The
area A of medium between the plates
·
According
to the gauss law, the electric field can be written as:
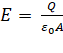
![]() = V
= V![]()
Since we know
that the capacitance is defined as V = Q/C, so capacitance can be rewritten as:
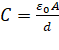
When the plates
are placed very close and the area of plates
are large we get the maximum capacitance.
Dielectric placed
between two electrodes
On the two plates, the
microscopic dipole moment of the material will shield the charges. Thus will
alter the effect of dielectric material which is inserted between the two
plates Materials have a permeability which is
given by the relative permeability k.
The capacitance
is thus given by:
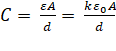
Capacitance of a parallel plate
capacitor can be increased by introducing dielectric between the plates as the
dielectric have permeability k, which is greater than 1. K is also sometimes
known as Dielectric Constant.
When in parallel plate capacitor
the area between the who plates are partially filled
with air and partially with other substance its Capacitance can be calculate.
Let there exist
a parallel plate capacitor in which medium between the parallel plates is
mainly the air and partially other substance as shown in figure below:
Dielectric and air
between plates
The arrangement of parallel plate
capacitor with dielectric material between them in groups fitting in each other
is known as Multi plate Parallel Plate
Capacitor.
Multi plate
Capacitor
The capacitance
of multi plate parallel plate capacitor can be calculated as:
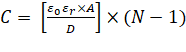
where,
A = Area of
each plate
ε0 =
Relative Permittivity of a Vacuum = 8.854 × 10-12 F/m
εr = Relative Permittivity of Dielectric
D = Distance
between plates
N = Number of
Plates
Let us assume
that a capacitor has capacitance C
and have electric charge Q and the
capacitor is electrically neutral
U = ![]() =
= ![]() QV
QV
Where, V is the potential difference
between the plates.
Now if the
charge upon the two plates of parallel plate capacitor are different, then
V1 will be the potential difference of plate 1 with
Q1 be the charge
While V2 will be the potential
difference of plate 2 with charge Q2
= −Q + δ Q
U = ![]() +
+ ![]()
= ![]() Q(V1 – V2)
+
Q(V1 – V2)
+ ![]()
U = 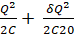
The electric
field is assumed from both the plates of parallel plate capacitor
E = ![]()
σ is the surface charge density on a single
side of the plate,
![]() , since half the charge will be on each side.
, since half the charge will be on each side.