Conductors and Insulators

In a conductor, electric current can flow freely, in an insulator it cannot. Metals such as copper typify conductors, while most non-metallic solids are said to be good insulators, having extremely high resistance to the flow of charge through them. "Conductor" implies that the outer electrons of the atoms are loosely bound and free to move through the material. Most atoms hold on to their electrons tightly and are insulators. In copper, the valence electrons are essentially free and strongly repel each other. Any external influence which moves one of them will cause a repulsion of other electrons which propagates, "domino fashion" through the conductor.

Simply stated, most metals are good electrical conductors, most non-metals are not. Metals are also generally good heat conductors while non-metals are not.

Insulators

Most solid materials are classified as insulators because they offer very large resistance to the flow of electric current. Metals are classified as conductors because their outer electrons are not tightly bound, but in most materials even the outermost electrons are so tightly bound that there is essentially zero electron flow through them with ordinary voltages. Some materials are particularly good insulators and can be characterized by their high resistivity :

	Resistivity (ohm m)
Glass	10^12
Mica	9 x 10^13
Quartz (fused)	5 x 10^16

Electrostatics of Conductors

Conductors contain mobile charge carriers. In metallic conductors, these charge carriers are electrons. In a metal, the outer (valence) electrons part away from their atoms and are free to move. These electrons are free within the metal but not free to leave the metal. The free electrons form a kind of ‘gas’; they collide with each other and with the ions, and move randomly in different directions. In an external electric field, they drift against the direction of the field. The positive ions made up of the nuclei and the bound electrons remain held in their fixed positions. In electrolytic conductors, the charge carriers are both positive and negative ions; but the situation in this case is more involved – the movement of the charge carriers is affected both by the external electric field as also by the so-called chemical forces .

1. Inside a conductor, electrostatic field is zero

Consider a conductor, neutral or charged. There may also be an external electrostatic field. In the static situation, when there is no current inside or on the surface of the conductor, the electric field is zero everywhere inside the conductor. This fact can be taken as the defining property of a conductor. A conductor has free electrons. As long as electric field is not zero, the free charge carriers would experience force and drift. In the static situation, the free charges have so distributed themselves that the electric field is zero everywhere inside. Electrostatic field is zero inside a conductor.

2. At the surface of a charged conductor, electrostatic field must be normal to the surface at every point

If E were not normal to the surface, it would have some non-zero component along the surface. Free charges on the surface of the conductor would then experience force and move. In the static situation, therefore, E should have no tangential component. Thus electrostatic field at the surface of a charged conductor must be normal to the surface at every point. (For a conductor without any surface charge density, field is zero even at the surface.)

3. The interior of a conductor can have no excess charge in the static situation

A neutral conductor has equal amounts of positive and negative charges in every small volume or surface element. When the conductor is charged, the excess charge can reside only on the surface in the static situation. This follows from the Gauss’s law. Consider any arbitrary volume element v inside a conductor. On the closed surface S bounding the volume element v, electrostatic field is zero. Thus the total electric flux through S is zero. Hence, by Gauss’s law, there is no net charge enclosed by S. But the surface S can be made as small as you like, i.e., the volume v can be made vanishingly small. This means there is no net charge at any point inside the conductor, and any excess charge must reside at the surface.

4. Electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface

This follows from results 1 and 2 above. Since E = 0 inside the conductor and has no tangential component on the surface, no work is done in moving a small test charge within the conductor and on its surface. That is, there is no potential difference between any two points inside or on the surface of the conductor. Hence, the result. If the conductor is charged, electric field normal to the surface exists; this means potential will be different for the surface and a point just outside the surface. In a system of conductors of arbitrary size, shape and charge configuration, each conductor is characterised by a constant value of potential, but this constant may differ from one conductor to the other.

5. Electric field at the surface of a charged conductor

where s is the surface charge density and ˆn is a unit vector normal to the surface in the outward direction.

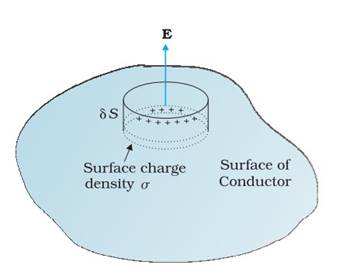
To derive the result, choose a pill box (a short cylinder) as the Gaussian surface about any point P on the surface, as shown in Fig above.

The pill box is partly inside and partly outside the surface of the conductor. It has a small area of cross section d S and negligible height. Just inside the surface, the electrostatic field is zero; just outside, the field is normal to the surface with magnitude E. Thus, the contribution to the total flux through the pill box comes only from the outside (circular) cross-section of the pill box. This equals ± EdS (positive for s > 0, negative for s < 0), since over the small area dS, E may be considered constant and E and dS are parallel or antiparallel. The charge enclosed by the pill box is sdS.

By Gauss’s law

ES =

E =

Including the fact that electric field is normal to the surface, we get the vector relation For s > 0, electric field is normal to the surface outward; for s < 0, electric field is normal to the surface inward.

6. Electrostatic shielding

Consider a conductor with a cavity, with no charges inside the cavity. A remarkable result is that the electric field inside the cavity is zero, whatever be the size and shape of the cavity and whatever be the charge on the conductor and the external fields in which it might be placed. We have proved a simple case of this result already: the electric field inside a charged spherical shell is zero. The proof of the result for the shell makes use of the spherical symmetry of the shell . But the vanishing of electric field in the (charge-free) cavity of a conductor is, as mentioned above, a very general result. A related result is that even if the conductor is charged or charges are induced on a neutral conductor by an external field, all charges reside only on the outer surface of a conductor with cavity.

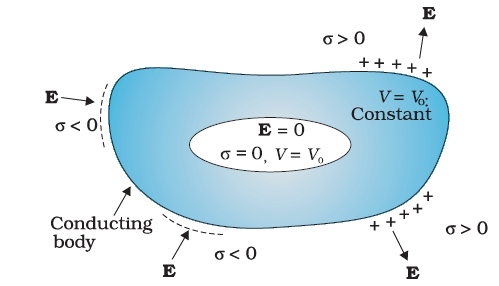
The proofs of the results noted in Fig above are omitted here, but we note their important implication. Whatever be the charge and field configuration outside, any cavity in a conductor remains shielded from outside electric influence: the field inside the cavity is always zero. This is known as electrostatic shielding. The effect can be made use of in protecting sensitive instruments from outside electrical influence.

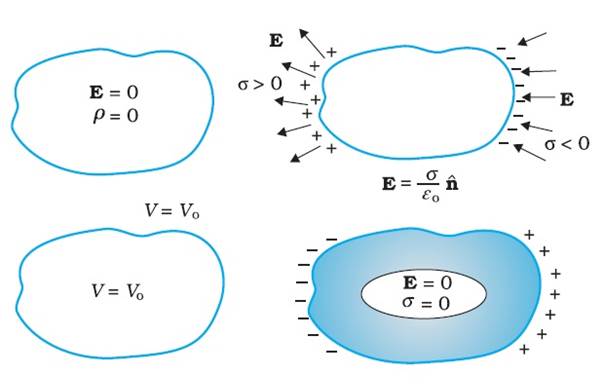
Above Figure gives a summary of the important electrostatic properties of a conductor.